5 1 Linear Equations and Functions Preview Warm

5 -1 Linear Equations and Functions Preview Warm Up California Standards Lesson Presentation

5 -1 Linear Equations and Functions Warm Up 1. Solve 2 x – 3 y = 12 for y. 2. Evaluate the function f(x) = 0, 5, and 10. f(– 10) = – 1 f(– 5) = 0 f(0) = 1 f(5) = 2 f(10) = 3 for – 10, – 5,

5 -1 Linear Equations and Functions California Standards 6. 0 Students graph a linear equation and compute x- and y- intercepts (e. g. graph 2 x + 6 y = 4). They are also able to sketch the region defined by linear inequalities (e. g. , they sketch the region defined by 2 x + 6 y < 4). Also covered: 7. 0, 18. 0

5 -1 Linear Equations and Functions Vocabulary linear equation linear function

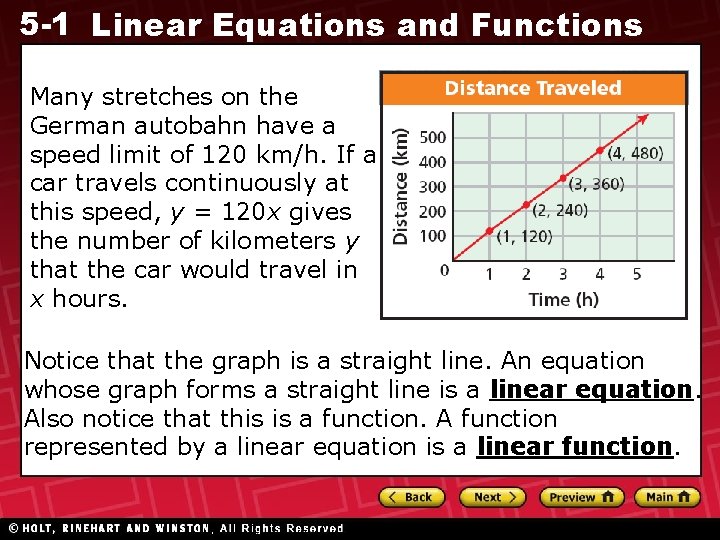
5 -1 Linear Equations and Functions Many stretches on the German autobahn have a speed limit of 120 km/h. If a car travels continuously at this speed, y = 120 x gives the number of kilometers y that the car would travel in x hours. Notice that the graph is a straight line. An equation whose graph forms a straight line is a linear equation. Also notice that this is a function. A function represented by a linear equation is a linear function.

5 -1 Linear Equations and Functions For any two points, there is exactly one line that contains them both. This means you need only two ordered pairs to graph a line. However, graphing three points is a good way to check that your line is correct.

5 -1 Linear Equations and Functions Additional Example 1 A: Graphing Linear Equations Graph y = 2 x + 1. Tell whether it represents a function. Step 1 Choose three values of x and generate ordered pairs. x y = 2 x + 1 (x, y) 1 y = 2(1) + 1 = 3 (1, 3) 0 y = 2(0) + 1 = 1 (0, 1) – 1 y = 2(– 1) + 1 = – 1 (– 1, – 1) Step 2 Plot the points and connect them with a straight line. No vertical line will intersect this graph more than once. So y = 2 x + 1 describes a function.

5 -1 Linear Equations and Functions Helpful Hint Sometimes solving for y first makes it easier to generate ordered pairs using values of x. To review solving for a variable, see Lesson 2 -6.

5 -1 Linear Equations and Functions Additional Example 1 B: Graphing Linear Equations Graph 15 x + 3 y = 9. Tell whether it represents a function. Step 1 Solve for y. 15 x + 3 y = 9 – 15 x 3 y = – 15 x + 9 Subtract 15 x from both sides. Since y is multiplied by 3 divide both sides by 3. y = – 5 x + 3

5 -1 Linear Equations and Functions Additional Example 1 B Continued Graph 15 x + 3 y = 9. Tell whether it represents a function. Step 2 Choose three values of x and generate ordered pairs x y = – 5 x + 3 (x, y) 1 y = – 5(1) + 3 = – 2 (1, – 2) 0 y = – 5(0) + 3 = 3 (0, 3) – 1 y = – 5(– 1) + 3 = 8 (– 1, 8) Step 3 Plot the points and connect them with a straight line. No vertical line will intersect this graph more than once. So 15 x + 3 y = 9 describes a function.

5 -1 Linear Equations and Functions Additional Example 1 C: Graphing Linear Equations Graph x = – 2. Tell whether it represents a function. Any ordered pair with an xcoordinate of – 2 will satisfy this equation. Plot several points that have an x-coordinate of – 2 and connect them with a straight line. There is a vertical line that intersects this graph more than once, so x = – 2 does not represent a function.

5 -1 Linear Equations and Functions Additional Example 1 D: Graphing Linear Equations Graph y = 8. Tell whether it represents a function. Any ordered pair with a y-coordinate of 8 will satisfy this equation. Plot several points that have an y-coordinate of 8 and connect them with a straight line. No vertical line will intersect this graph more than once, so y = 8 represents a function.

5 -1 Linear Equations and Functions Check It Out! Example 1 a Graph y = 4 x. Tell whether it represents a function. Step 1 Choose three values of x and generate ordered pairs x y = 4 x (x, y) 1 y = 4(1) = 4 (1, 4) 0 y = 4(0) = 0 (0, 0) – 1 y = 4(– 1) = – 4 (– 1, – 4) Step 2 Plot the points and connect them with a straight line. No vertical line will intersect this graph more than once. So y = 4 x describes a function.

5 -1 Linear Equations and Functions Check It Out! Example 1 b Graph y + x = 7. Tell whether it represents a function. Step 1 Solve for y. y+x=7 –x –x y = –x + 7 Subtract x from both sides.

5 -1 Linear Equations and Functions Check It Out! Example 1 b Continued Graph y + x = 7. Tell whether it represents a function. Step 2 Choose three values of x and generate ordered pairs x y = –x + 7 (x, y) 1 y = –(1) + 7 = 6 (1, 6) 0 y = –(0) + 7 = 7 (0, 7) – 1 y = –(– 1) + 7 = 8 (– 1, 8) Step 3 Plot the points and connect them with a straight line. No vertical line will intersect this graph more than once. So y + x = 7 describes a function.

5 -1 Linear Equations and Functions Check It Out! Example 1 c Graph function. . Tell whether it represents a Any ordered pair with an xcoordinate of will satisfy this equation. Plot several points that have an x-coordinate of and connect them with a straight line. There is a vertical line that intersects this graph more than once, so x = does not describe a function.

5 -1 Linear Equations and Functions

5 -1 Linear Equations and Functions Additional Example 2 A: Determining Whether a Point is on a Graph Without graphing, tell whether each point is on the graph of 2 x + 5 y = 16. (3, 2) Substitute: 2 x + 5 y = 16 ? 2(3) + 5(2) =16 ? 6 + 10 = 16 16 = 16 Since (3, 2) is a solution to 2 x + 5 y = 16, (3, 2) is on the graph.

5 -1 Linear Equations and Functions Additional Example 2 B: Determining Whether a Point is on a Graph Without graphing tell whether each point is on the graph of 2 x + 5 y = 16. (2, 2) Substitute: 2 x + 5 y = 16 ? 2(2) + 5(2) = 16 ? 4 + 10 = 16 14 16 Since (2, 2) is not a solution to 2 x + 5 y = 16, (2, 2) is not on the graph.

5 -1 Linear Equations and Functions Additional Example 2 C: Determining Whether a Point is on a Graph Without graphing tell whether each point is on the graph of 2 x + 5 y = 16. (8, 0) Substitute: 2 x + 5 y = 16 ? 2(8) + 5(0) = 16 ? 16 + 0 = 16 16 = 16 Since (8, 0) is a solution to 2 x + 5 y = 16, (8, 0) is on the graph.

5 -1 Linear Equations and Functions Check It Out! Example 2 a Without graphing tell whether each point is on the graph of x – 3 y = 12. (5, 1) Substitute: x – 3 y = 12 ? 5 – 3(1) = 12 ? 5 – 3 = 12 2 12 Since (5, 1) is not a solution to x – 3 y = 12, (5, 1) is not on the graph.

5 -1 Linear Equations and Functions Check It Out! Example 2 b Without graphing tell whether each point is on the graph of x – 3 y = 12. (0, – 4) Substitute: x – 3 y = 12 ? 0 – 3(– 4) = 12 ? 0 + 12 = 12 Since (0, – 4) is a solution to x – 3 y = 12, (0, – 4) is on the graph.

5 -1 Linear Equations and Functions Check It Out! Example 2 c Without graphing tell whether each point is on the graph of x – 3 y = 12. (1. 5, – 3. 5) Substitute: x – 3 y = 12 ? 1. 5 – 3(– 3. 5) = 12 ? 1. 5 + 10. 5 = 12 12 = 12 Since (1. 5, – 3. 5) is a solution to x – 3 y = 12, (1. 5, – 3. 5) is on the graph.

5 -1 Linear Equations and Functions Linear equations can be written in the standard form as shown below.

5 -1 Linear Equations and Functions Notice that when a linear equation is written in standard form. • x and y both have exponents of 1. • x and y are not multiplied together. • x and y do not appear in denominators, exponents, or radical signs.

5 -1 Linear Equations and Functions

5 -1 Linear Equations and Functions Additional Example 3 A: Writing Linear Equations in Standard Form Write x = 2 y + 4 in standard form and give the values of A, B, and C. Then describe the graph. x = 2 y + 4 – 2 y x – 2 y = 4 Subtract 2 y from both sides. The equation is in standard form. A = 1, B = – 2, C = 4 The graph is a line that is neither horizontal nor vertical.

5 -1 Linear Equations and Functions Additional Example 3 B: Writing Linear Equations in Standard Form Write x = 4 in standard form and give the values of A, B, and C. Then describe the graph. x=4 x + 0 y = 4 The equation is in standard form. A = 1, B = 0, C = 4 The graph is a vertical line at x = 4.

5 -1 Linear Equations and Functions Check It Out! Example 3 a Write y = 5 x – 9 in standard form and give the values of A, B, and C. Then describe the graph. y = 5 x – 9 – 5 x + y = – 9 Subtract 5 x from both sides. The equation is in standard form. A = – 5, B = 1, C = – 9 The graph is a line that is neither horizontal nor vertical.

5 -1 Linear Equations and Functions Check It Out! Example 3 b Write y = 12 in standard form and give the values of A, B, and C. Then describe the graph. y = 12 0 x + y = 12 The equation is in standard form. A = 0, B = 1, C = 12 The graph is a horizontal line at y = 12.

5 -1 Linear Equations and Functions Check It Out! Example 3 c Write x = 2 in standard form and give the values of A, B, and C. Then describe the graph. x=2 x + 0 y = 2 The equation is in standard form. A = 1, B = 0, C = 2 The graph is a vertical line at x = 2.

5 -1 Linear Equations and Functions Remember! • y – x = y + (–x) • y +(–x) = –x + y • –x = – 1 x • y = 1 y

5 -1 Linear Equations and Functions For linear functions whose graphs are not horizontal, the domain and range are all real numbers. However, in many real-world situations, the domain and range must be restricted. For example, some quantities cannot be negative, such as distance.

5 -1 Linear Equations and Functions Sometimes domain and range are restricted even further to a set of points. For example, a quantity such as number of people can only be whole numbers. When this happens, the graph is not actually connected because every point on the line is not a solution. However, you may see these graphs shown connected to indicate that the linear pattern, or trend, continues.

5 -1 Linear Equations and Functions Additional Example 4: Application The relationship between human years and dog years is given by the function y = 7 x, where x is the number of human years. Graph this function and give its domain and range. Choose several values of x and make a table of ordered pairs. x y = 7 x (x, y) 2 y = 7(2) = 14 (2, 14) 4 y = 7(4) = 28 (4, 28) 6 y = 7(6) = 42 (6, 42) The ages are continuous starting with 0, so the domain is: {x ≥ 0} and the range is: {y ≥ 0}.

5 -1 Linear Equations and Functions Additional Example 4 Continued Graph the ordered pairs. Human Years vs. Dog Years (6, 42) (4, 28) (2, 14) Any point on the line is a solution in this situation. The arrow shows that the trend continues.

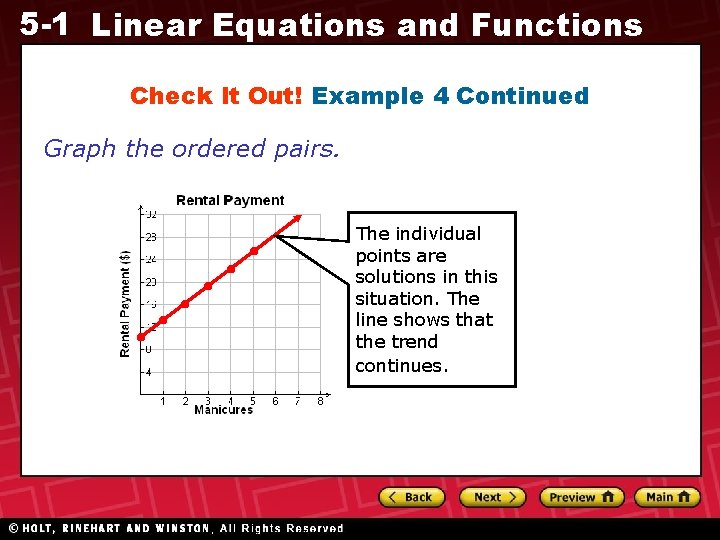
5 -1 Linear Equations and Functions Check It Out! Example 4 What if…? At another salon, Sue can rent a station for $10. 00 per day plus $3. 00 per manicure. The amount she would pay each day is given by f(x) = 3 x + 10, where x is the number of manicures. Graph this function and give its domain and range.

5 -1 Linear Equations and Functions Check It Out! Example 4 Continued Choose several values of x and make a table of ordered pairs. x f(x) = 3 x + 10 0 f(0) = 3(0) + 10 = 10 1 f(1) = 3(1) + 10 = 13 2 f(2) = 3(2) + 10 = 16 3 f(3) = 3(3) + 10 = 19 4 f(4) = 3(4) + 10 = 22 5 f(5) = 3(5) + 10 = 25 The number of manicures must be a whole number, so the domain is {0, 1, 2, 3, …}. The range is {10, 13, 16, 19, …}.

5 -1 Linear Equations and Functions Check It Out! Example 4 Continued Graph the ordered pairs. The individual points are solutions in this situation. The line shows that the trend continues.

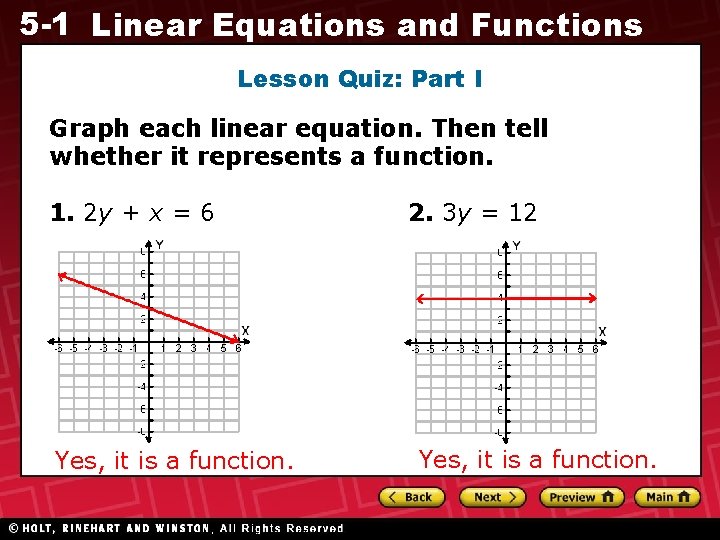
5 -1 Linear Equations and Functions Lesson Quiz: Part I Graph each linear equation. Then tell whether it represents a function. 1. 2 y + x = 6 Yes, it is a function. 2. 3 y = 12 Yes, it is a function.

5 -1 Linear Equations and Functions Lesson Quiz: Part II Without graphing, tell whether each point is on the graph of 6 x – 2 y = 8. 3. (1, 1) no 4. (3, 5) yes 5. The cost of a can of iced-tea mix at Save. More Grocery is $4. 75. The function f(x) = 4. 75 x gives the cost of x cans of iced-tea mix. Graph this function and give its domain and range. D: {0, 1, 2, 3, …} R: {0, 4. 75, 9. 50, 14. 25, …}