5 1 Graphing Sine and Cosine Functions When

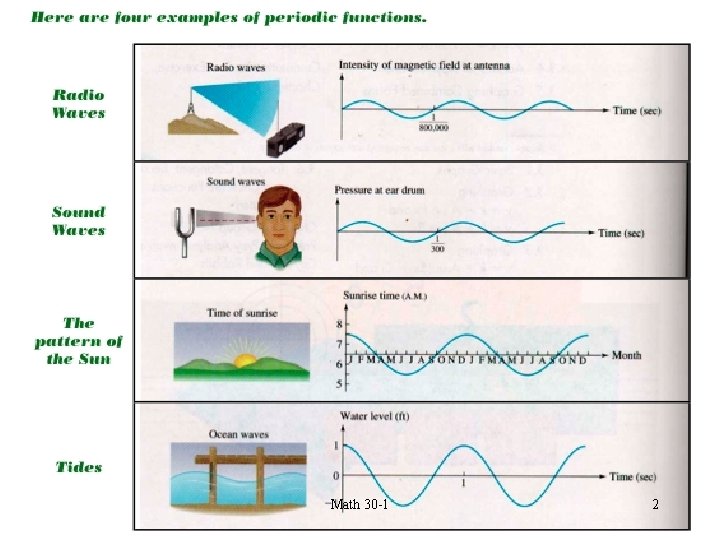
5. 1 Graphing Sine and Cosine Functions When Function values repeat at regular intervals the function could be referred to as a cyclic function or periodic function. You can model these types of behaviour with sine or cosine functions. Math 30 -1 1

Math 30 -1 2

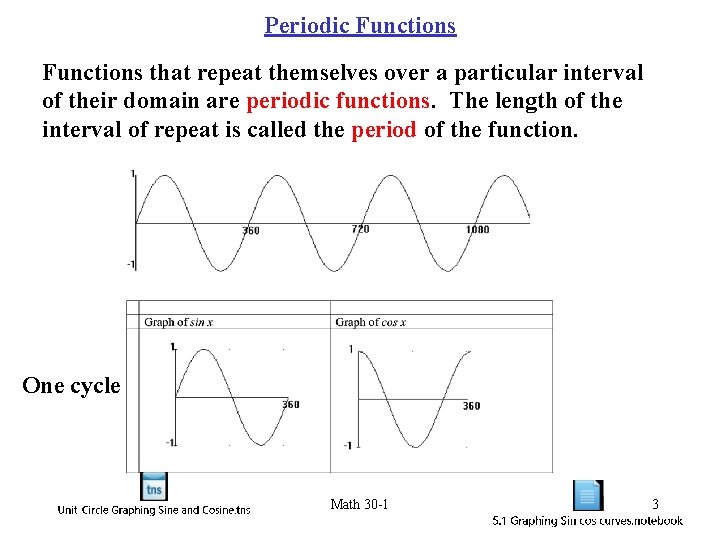
Periodic Functions that repeat themselves over a particular interval of their domain are periodic functions. The length of the interval of repeat is called the period of the function. One cycle Math 30 -1 3

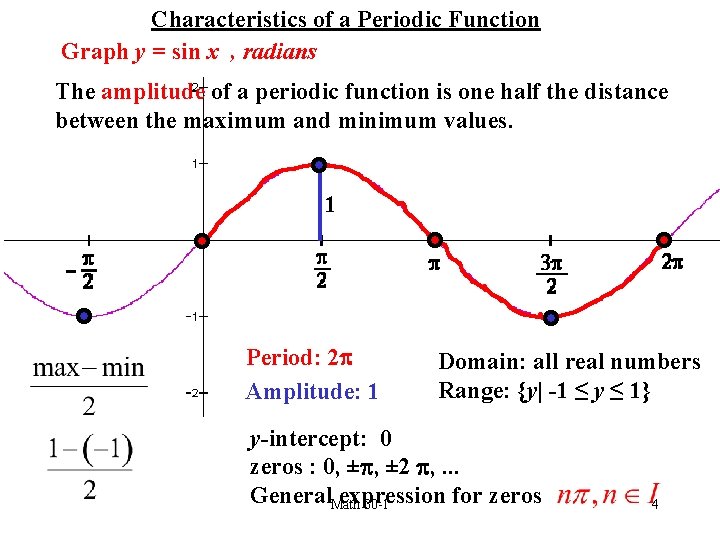
Characteristics of a Periodic Function Graph y = sin x , radians The amplitude of a periodic function is one half the distance between the maximum and minimum values. 1 Period: 2 Amplitude: 1 Domain: all real numbers Range: {y| -1 ≤ y ≤ 1} y-intercept: 0 zeros : 0, ± 2 , . . . General. Math expression for zeros 30 -1 4

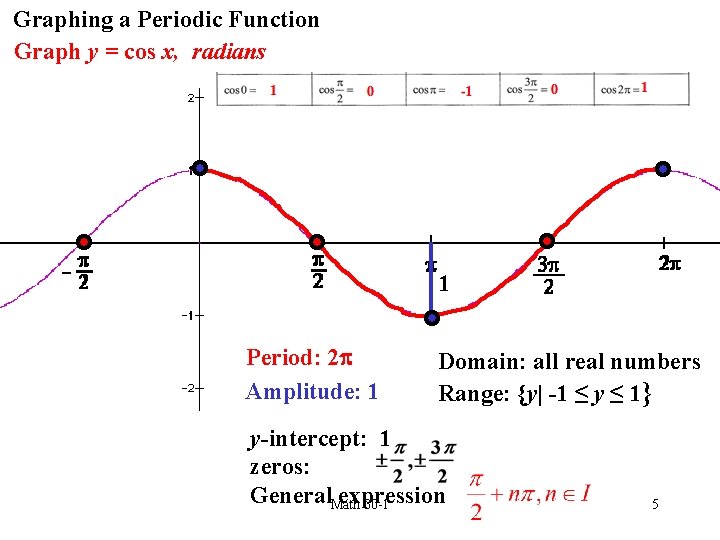
Graphing a Periodic Function Graph y = cos x, radians 1 Period: 2 Amplitude: 1 Domain: all real numbers Range: {y| -1 ≤ y ≤ 1} y-intercept: 1 zeros: General. Math expression 30 -1 5

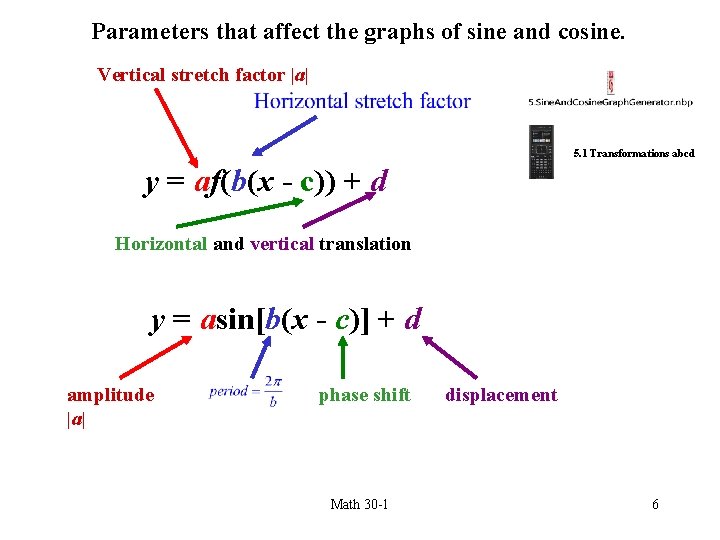
Parameters that affect the graphs of sine and cosine. Vertical stretch factor |a| 5. 1 Transformations abcd y = af(b(x - c)) + d Horizontal and vertical translation y = asin[b(x - c)] + d amplitude |a| phase shift Math 30 -1 displacement 6

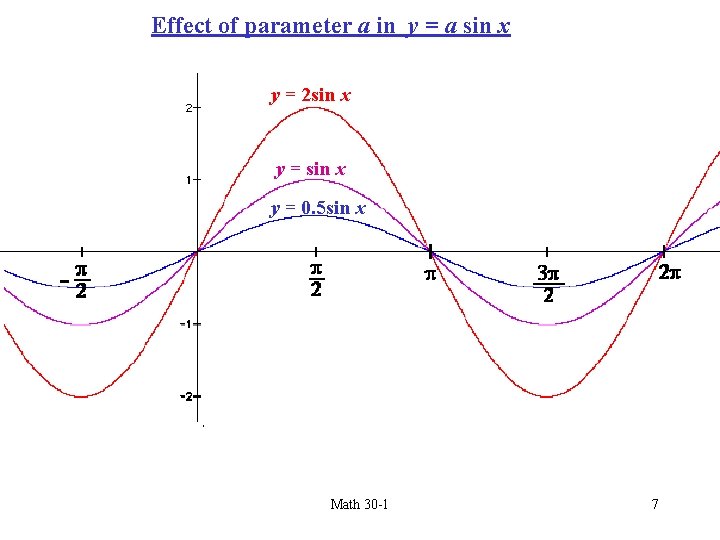
Effect of parameter a in y = a sin x Graph y = 2 siny x= 2 sin x and y = 0. 5 sin x. sinxx yy==sin y = 0. 5 sin x Math 30 -1 7

Comparing the Graphs of y = a sin x y = sin x Period Amplitude Domain Range y = 2 sin x y = 0. 5 sin x 2 2 2 1 2 0. 5 All real numbers {-1 ≤ y ≤ 1} {-2 ≤ y ≤ 2} All real numbers {-0. 5 ≤ y ≤ 0. 5} Zeros The amplitude of the graph of y = a sin x is | a |. When a > 0, there is a vertical stretch by a factor of |a|. When a < 0, there is a vertical stretch by a factor of |a| and a reflection in the x-axis. Math 30 -1 8

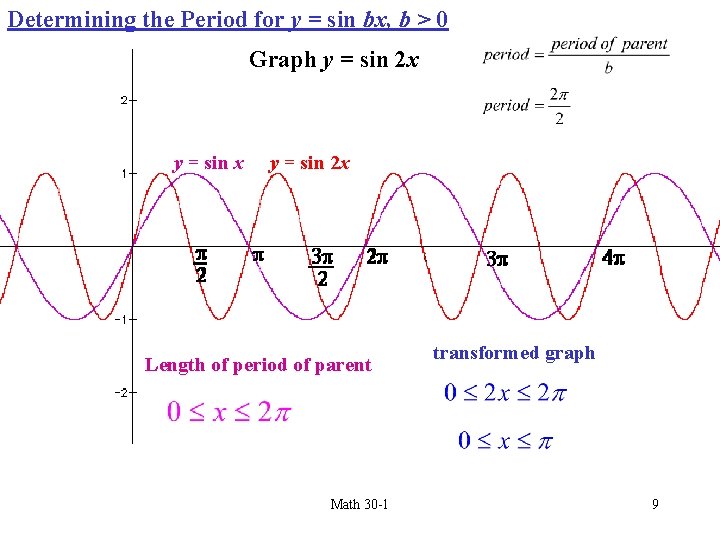
Determining the Period for y = sin bx, b > 0 Graph y = sin 2 x y = sin 2 x Length of period of parent Math 30 -1 transformed graph 9

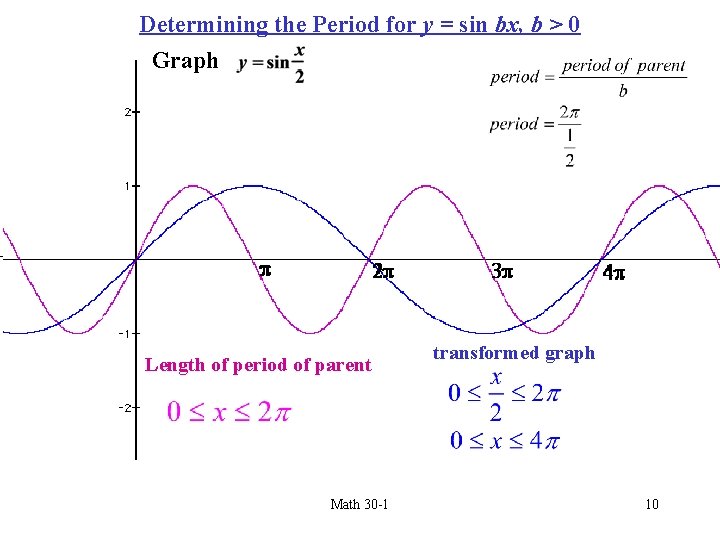
Determining the Period for y = sin bx, b > 0 Graph y = sin x Length of period of parent Math 30 -1 transformed graph 10

Comparing the Graphs of y = sin bx y = sin x Period Amplitude Domain Range y = sin 2 x y = sin 0. 5 x 2 4 1 1 1 All real numbers {-1 ≤ y ≤ 1} Zeros The period for y = sin bx is When b > 0, there is a horizontal stretch by a factor of 1/|b|. Math 30 -1 11 When b < 0, there is a reflection and a horizontal stretch of 1/|b|.

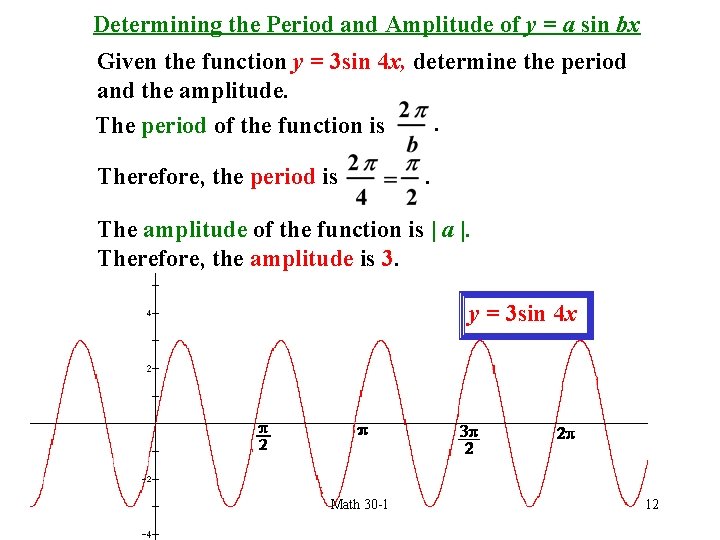
Determining the Period and Amplitude of y = a sin bx Given the function y = 3 sin 4 x, determine the period and the amplitude. . The period of the function is Therefore, the period is . The amplitude of the function is | a |. Therefore, the amplitude is 3. y = 3 sin 4 x Math 30 -1 12

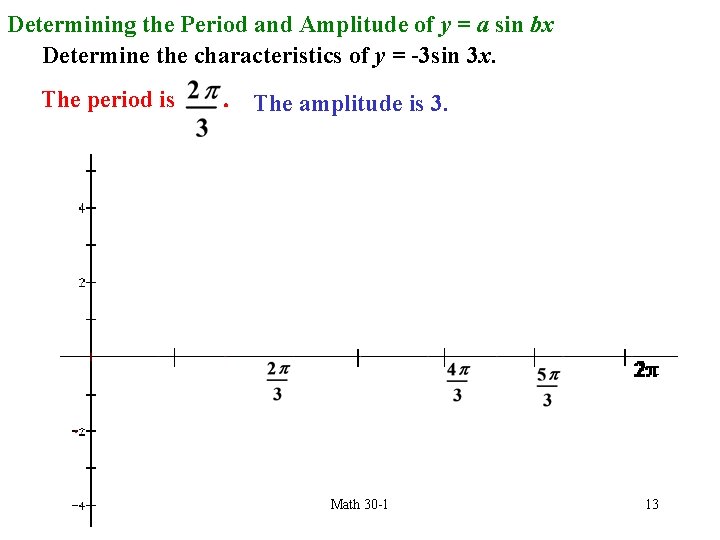
Determining the Period and Amplitude of y = a sin bx Determine the characteristics of y = -3 sin 3 x. The period is . The amplitude is 3. Math 30 -1 13

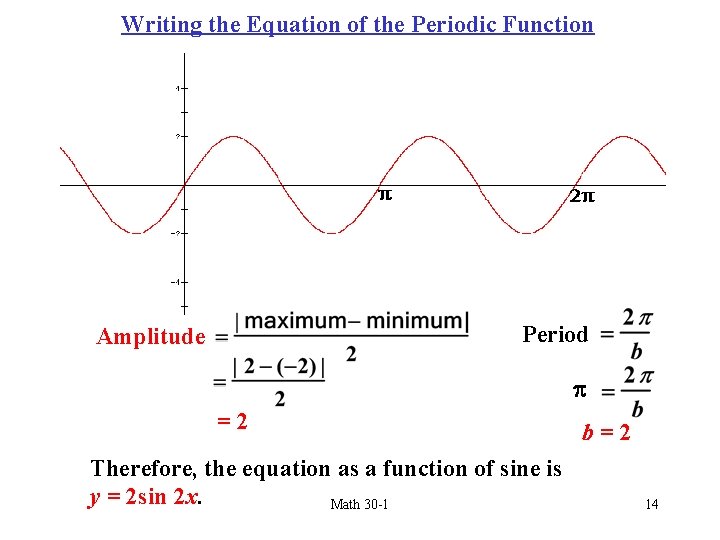
Writing the Equation of the Periodic Function Period Amplitude =2 Therefore, the equation as a function of sine is y = 2 sin 2 x. Math 30 -1 b=2 14

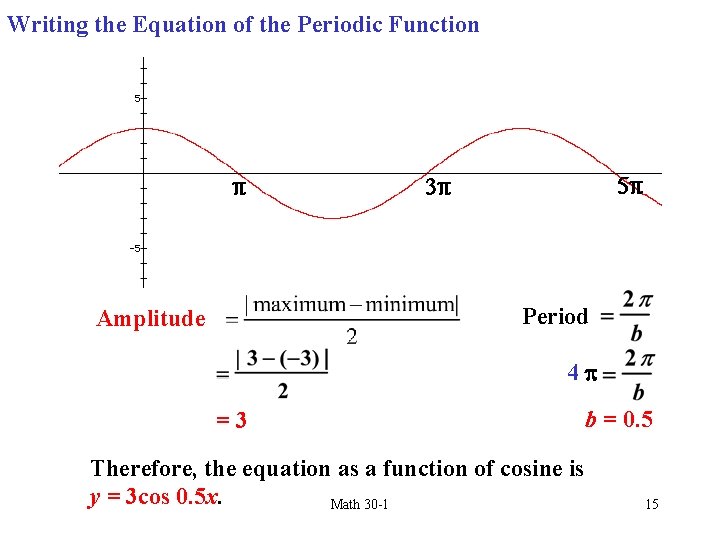
Writing the Equation of the Periodic Function Period Amplitude 4 =3 Therefore, the equation as a function of cosine is y = 3 cos 0. 5 x. Math 30 -1 b = 0. 5 15

Suggested Questions: Pages 233 1, 2, 4, 5, 6, 8, 10, 11 b, c 14, 17 a, 20, C 4 Math 30 -1 16