4 TREES 4 1 Preliminaries 4 2 Binary

4. TREES

4. 1. Preliminaries 4. 2. Binary Trees 4. 3. The Search Tree ADT - Binary Search Trees 4. 4. AVL Trees 4. 5. Splay Trees 4. 6. Tree Traversals (Revisited) 4. 7. B-Trees 3

• root ของ subtree เรยกวาเปน child ของ r, และ r เปน parent ของ root แตละ root ของ subtree T 1 T 2 T 3 T 4 … T 10 Figure 4. 1 Typical tree using the recursive definition • จากคำนยามแบบ recursive ของ tree เราพบวา tree เปน collection ของ node 5

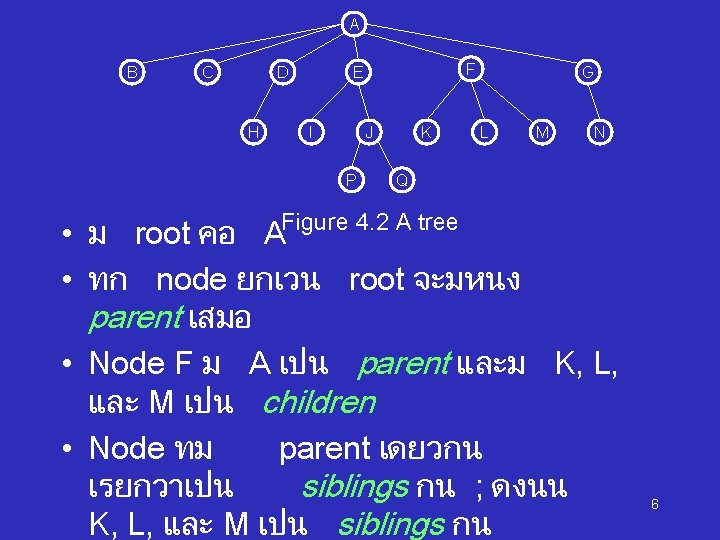
• height ของ ni คอ path ทยาวทสดจาก ni ไปยง leaf ใด ๆ ดงนน ทก ๆ leaves จงม height เปน 0 The height of a tree height of the root = The • ในรป Figure 4. 2, – E ม depth = 1, height = 2 –F ม depth = 1 และ height = 1 8

Terminology used in trees • Root: The top node in a tree. • Child : A node directly connected to another node when moving away from the Root. • Parent : The converse notion of a child. • Siblings : A group of nodes with the same parent. • Descendant : A node reachable by repeated proceeding from parent to child. • Ancestor : A node reachable by repeated proceeding from child to parent. • Leaf (less commonly called External node) : A node with no children. • Branch, Internal node : A node with at least one child. • Degree : The number of sub trees of a node. • Edge : The connection between one node and another. • Path : A sequence of nodes and edges connecting a node with a descendant. • Level : The level of a node is defined by 1 + (the number of connections between the node and the root). • Height of node : The height of a node is the number of edges on 9 the longest path between that node and a leaf.

4. 1. 1 Implementation of Trees children แตละโนดถกเกบอยใน linked list ของ tree nodes class Tree. Node { Object element; Tree. Node irst. Child; Tree. Node next. Sibling; }; 10

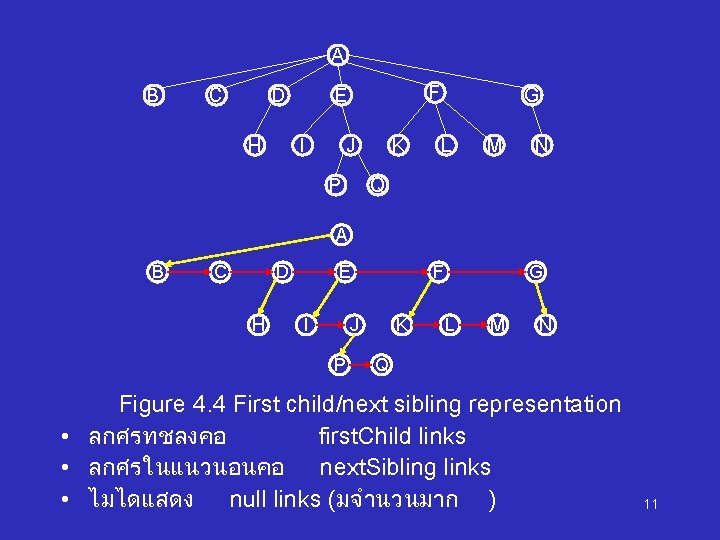
A B C D H F E I J P K G L M N Q A B C D H E I F J P K G L M N Q Figure 4. 4 First child/next sibling representation • ลกศรทชลงคอ first. Child links • ลกศรในแนวนอนคอ next. Sibling links • ไมไดแสดง null links (มจำนวนมาก ) 11

4. 1. 2 Tree Traversals with an Application มการประยกตใช trees ในงานตาง ๆ มาก ทนยมใชกนอยางหนงคอใน โครงสราง directory ใน operating systems ตางๆ เชนใน UNIX, VAX/VMS, และ DOS /usr* mark* book* ch 1. r ch 2. r ch 3. r alex* course* junk. c work* cop 3530* syl. r course* cop 3212* fall 88* spr 89* sum 89* syl. r junk. c bill* fall 88* grades prog 1. r prog 2. r fall 89* prog 2. r prog 1. r grades 12

ตวอยางเชนตองการแสดงรายการช อของ filesใน directory โดยใหแสดงชอ file ดวยการยอยหนาเขา di ถา file นนอยใน directory ทมระดบ depth เปน di : /*1*/ /*2*/ /*3*/ /*4*/ private void list. All(int dept) { print. Name( dept ); // Print the name if ( is. Directory() ) for each file c in this directory c. list. All( dept + 1 ); } public void list. All() { 13

/usr* mark* book* ch 1. r ch 2. r ch 3. r alex* course* junk. c work* cop 3530* syl. r course* cop 3212* fall 88* spr 89* sum 89* syl. r junk. c bill* fall 88* grades prog 1. r prog 2. r • routine เรมตนดวยชอ directory ทม depth เปน 0, คอไมตองยอหนาสำหรบ root • ถารายการทอานเปน directory กจะทำการประมวลผล children ทงหมดในแบบ recursive ทละตว children เหลานอยลกลงไปหนงระด fall 89* prog 2. r prog 1. r grades /usr mark book ch 1. r ch 2. r ch 3. r courses cop 3530 fall 88 syl. r spr 89 syl. r sum 89 syl. r junk. c alex junk. c bill work course cop 3212 fall 88 grade prog 1. r prog 2. r fall 89 prog 1. r prog 2. r grade 14

/usr*(1) mark*(1) book*(1) alex*(1) bill*(1) course*(1) junk. c(6) junk. c(8) work*(1) course*(1) ch 1. r(3)ch 2. r(2)ch 3. r(4)cop 3530*(1) fall 88*(1)spr 89*(1)sum 89*(1) cop 3212*(1) fall 88*(1) fall 89*(1) syl. r(5) syl. r(2) grades(3)prog 1. r(4)prog 2. r(1) prog 2. r(2)prog 1. r(7)grades(9) Figure 4. 8 วธการปกต คอ หาจำนวน blocks ใน subdirectories กอน และจำนวน blocks ทงหมดเทากบจำนวนบลอกท งหมดใน subdirectories 17

/*1*/ /*2*/ /*3*/ /*4*/ /*5*/ public int size() { int total. Size = size. Of. This. File; if ( is. Directory() ) for each file c in this directory; total. Size += c. size(); return( total. Size ); } Figure 4. 9 18

ถา object ขณะนนไมใช directory กใหคากลบเปน จำนวน blocks ทใช มฉะนน (กจะเปน directory) กจะรวมจำนวนบล อกทใชโดย directory เขากบจำนวนบล ch 1. r ch 2. r chr. 3 book syl. r fall 88 syl. r spr 89 syl. r sum 89 cop 3530 course junk. c mark junk. c alex work grades prog 1. r prog 2. r fall 88 prog 2. r prog 1. r grades fall 89 cop 3212 course bill /usr 3 2 4 10 1 2 5 6 2 3 12 13 6 30 8 9 1 3 4 1 9 2 7 9 19 29 30 32 72 19

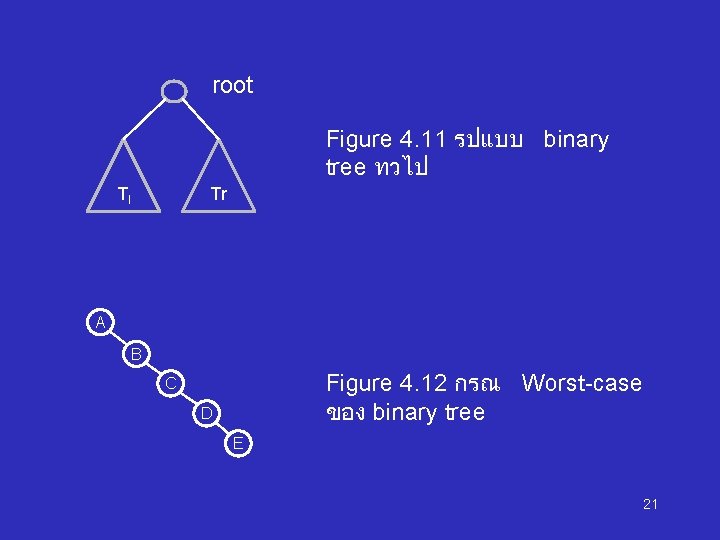
root Figure 4. 11 รปแบบ binary tree ทวไป Tl Tr A B Figure 4. 12 กรณ Worst-case ของ binary tree C D E 21

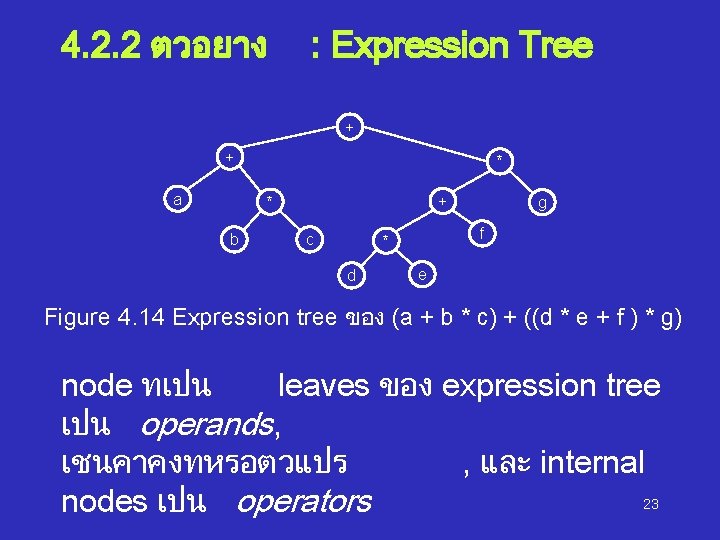
4. 2. 2 ตวอยาง : Expression Tree + + a * + * b c f * d g e Figure 4. 14 Expression tree ของ (a + b * c) + ((d * e + f ) * g) node ทเปน leaves ของ expression tree เปน operands, เชนคาคงทหรอตวแปร , และ internal 23 nodes เปน operators

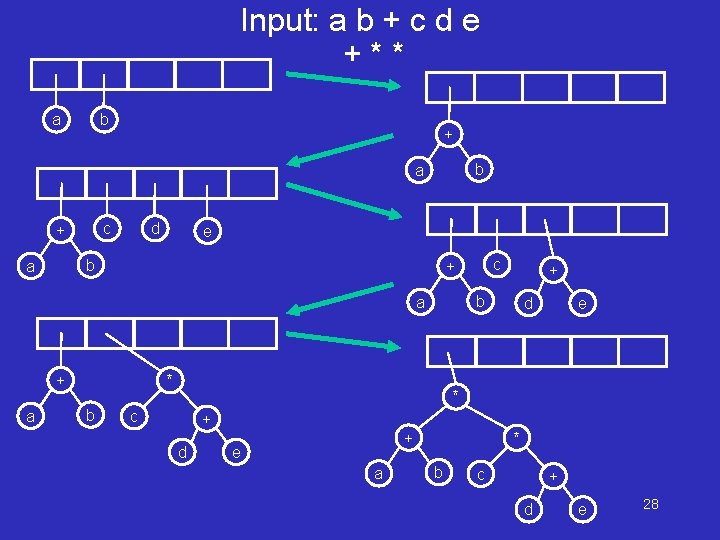
Input: a b + c d e +** a b + b a c + d e b a + * b + b a a c + d e * c + d + e a * b c + d e 28

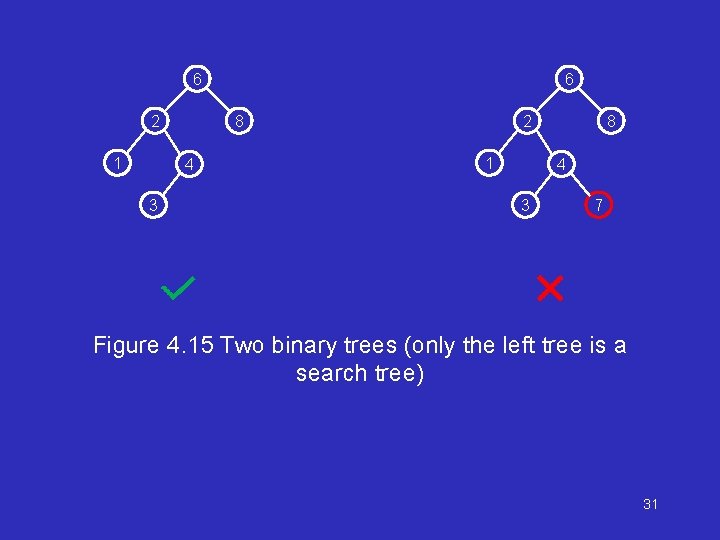
6 2 1 8 4 3 7 Figure 4. 15 Two binary trees (only the left tree is a search tree) 31

class Binary. Node { // Constructors Binary. Node( Comparable the. Element ) { this( the. Element, null ); } Binary. Node( Comparable the. Element, Binary. Node lt, Binary. Node rt ) { element = the. Element; left = lt; right = rt; } // Friendly data; accessible by other package routines Comparable element; // The data in the node Binary. Node left; // Left child Binary. Node right; // Right child } Figure 4. 16 The Binary. Node class 33

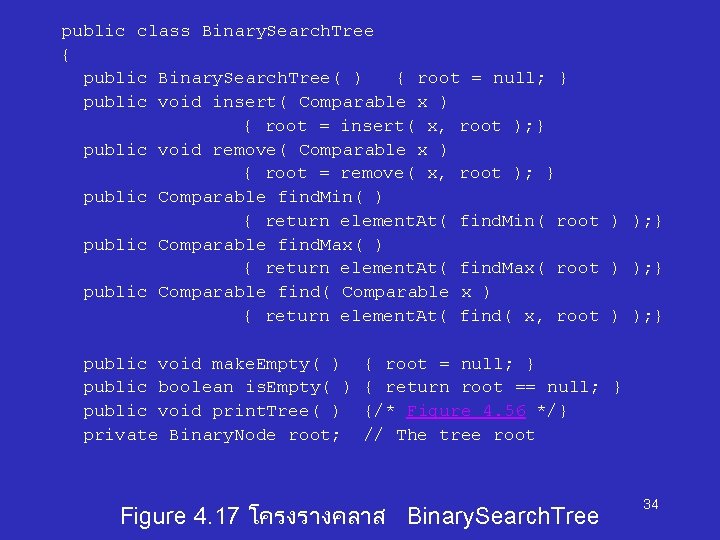
public class Binary. Search. Tree { public Binary. Search. Tree( ) { root = null; } public void insert( Comparable x ) { root = insert( x, root ); } public void remove( Comparable x ) { root = remove( x, root ); } public Comparable find. Min( ) { return element. At( find. Min( root ) ); } public Comparable find. Max( ) { return element. At( find. Max( root ) ); } public Comparable find( Comparable x ) { return element. At( find( x, root ) ); } public void make. Empty( ) public boolean is. Empty( ) public void print. Tree( ) private Binary. Node root; { root = null; } { return root == null; } {/* Figure 4. 56 */} // The tree root Figure 4. 17 โครงรางคลาส Binary. Search. Tree 34

private Comparable element. At( Binary. Node t ) { return t == null ? null : t. element; } private Binary. Node find( Comparable x, Binary. Node t ) {/* Figure 4. 18 */} private Binary. Node find. Min( Binary. Node t ) {/* Figure 4. 19 */} private Binary. Node find. Max( Binary. Node t ) {/* Figure 4. 20 */} private Binary. Node insert( Comparable x, Binary. Node t ) {/* Figure 4. 22 */ } private Binary. Node remove( Comparable x, Binary. Node t ) {/* Figure 4. 25 */ } private void print. Tree( Binary. Node t ) {/* Figure 4. 56 */} } Figure 4. 17 โครงรางคลาส Binary. Search. Tree 35

/*** Internal method to find an item in a subtree. * x is item to search for. * t the node that roots the tree. * @return node containing the matched item */ private Binary. Node find( Comparable x, Binary. Node t ) { if( t == null ) return null; if( x. compare. To( t. element ) < 0 ) return find( x, t. left ); else if( x. compare. To( t. element ) > 0 ) return find( x, t. right ); else return t; // Match } Figure 4. 18 Find operation 37

/*** Internal method to find the smallest item * in a subtree. * @param t the node that roots the tree. * @return node containing the smallest item. */ private Binary. Node find. Min( Binary. Node t ) { if ( t == null ) return null; else if ( t. left == null ) return t; return find. Min ( t. left ); } Figure 4. 19 find. Min 39

/*** Internal method to find the largest item * in a subtree. * @param t the node that roots the tree. * @return node containing the largest item. */ private Binary. Node find. Max( Binary. Node t ) { if( t != null ) while( t. right != null ) t = t. right; return t; } Figure 4. 20 find. Max 40

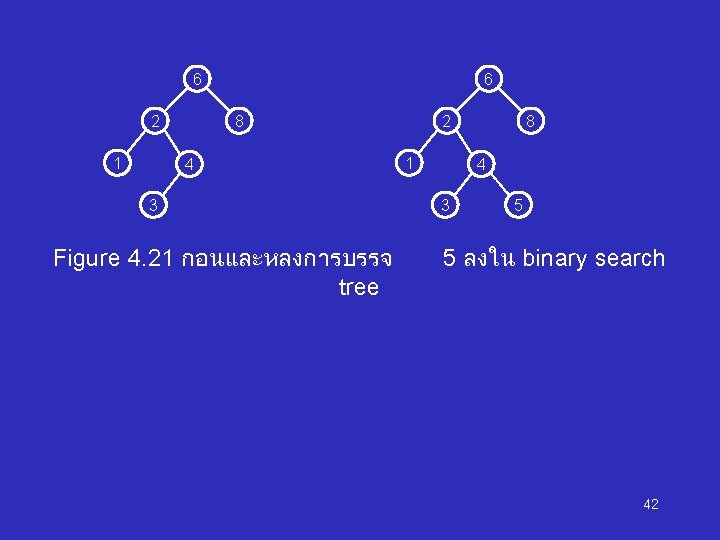
6 2 1 6 8 4 3 Figure 4. 21 กอนและหลงการบรรจ tree 2 1 8 4 3 5 5 ลงใน binary search 42

/** x the item to insert. * t the node that roots the tree. * @return the new root. */ private Binary. Node insert( Comparable x, Binary. Node t ) { /* 1*/ if( t == null ) /* 2*/ t = new Binary. Node( x, null ); /* 3*/ else if( x. compare. To( t. element ) < 0 ) /* 4*/ t. left = insert( x, t. left ); /* 5*/ else if( x. compare. To( t. element ) > 0 ) /* 6*/ t. right = insert( x, t. right ); /* 7*/ else /* 8*/ ; // Duplicate; do nothing /* 9*/ return t; } Figure 4. 22 Insertion 43

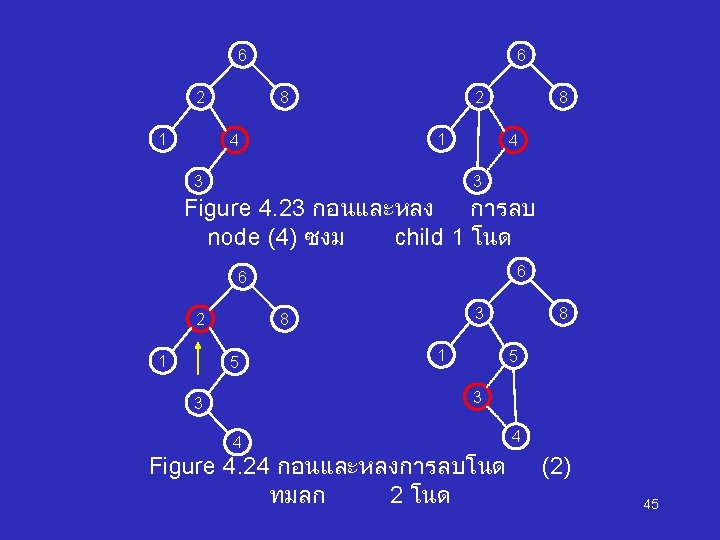
private Binary. Node remove( Comparable x, Binary. Node t ) { if( t == null ) return t; // Item not found; do nothing if( x. compare. To( t. element ) < 0 ) t. left = remove( x, t. left ); else if( x. compare. To( t. element ) > 0 ) t. right = remove( x, t. right ); else if( t. left != null && t. right != null ) // Two children { t. element = find. Min( t. right ). element; t. right = remove( t. element, t. right ); } else t = ( t. left != null ) ? t. left : t. right; return t; } Figure 4. 25 Deletion routine 46

การสราง tree ขนาด 500 โนด โดยการสรางแบบสม ได tree ม expected depth 9. 98 Figure 4. 26 A randomly generated binary search tree 50