4 The Grand Canonical Ensemble 1 Equilibrium between

4. The Grand Canonical Ensemble 1. Equilibrium between a System & a Particle-Energy Reservoir 2. A System in the Grand Canonical Ensemble 3. Physical Significance of Various Statistical Quantities 4. Examples 5. Density & Energy Fluctuations in the Grand Canonical Ensemble: Correspondence with Other Ensembles 6. Thermodynamic Phase Diagrams 7. Phase Equilibrium & the Clausius-Clapeyron Equation

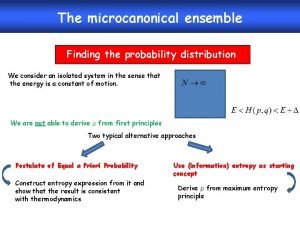
4. 1. Equilibrium between a System & a Particle-Energy Reservoir System A immersed in particle-energy reservoir A. A in microstate with Nr & Es with Using

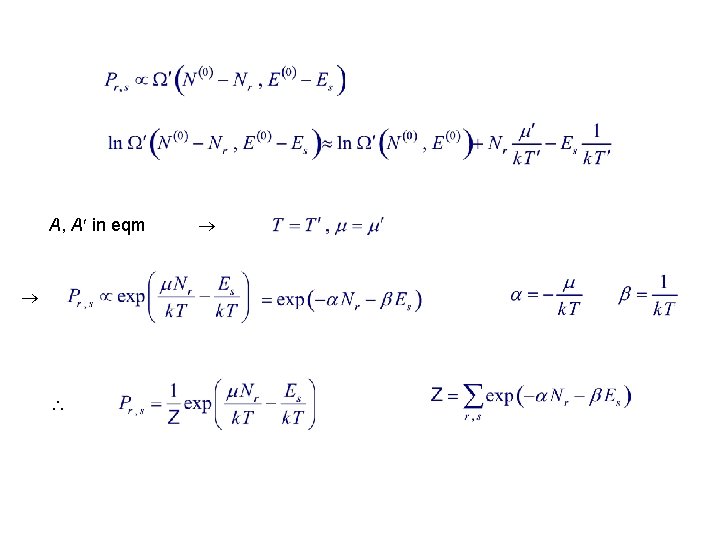
A, A in eqm

4. 2. A System in the Grand Canonical Ensemble Consider ensemble of N identical systems sharing particles & energy Let nr, s = # of systems with Nr & Es , then Let W { nr, s } = # of ways to realize a given set of distribution { nr, s }. Method of Most Probable Values : Let { nr, s* } = most probable set of distribution, i. e. ,

Method of Mean Values : (X) means sum includes only terms that satisfy constraint on X. Saddle point method For a given Classical mech (Gibb –corrected ): the parameters & are determined from

4. 3. Physical Significance of Various Statistical Quantities The q-potential is defined as d. Es caused by d. V.

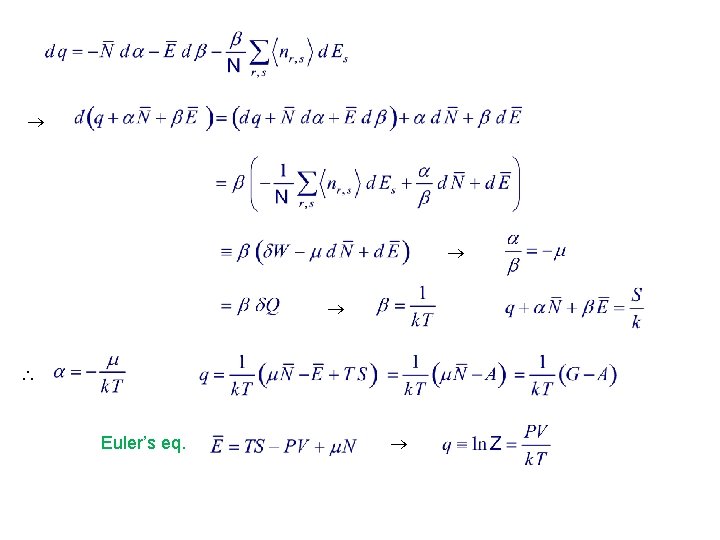
Euler’s eq.

Fugacity Variable dependence : Grand partition function Note: Z is much easier to evaluate than Z, especially for quantum statistics and/or interacting systems.

Grand Potential Approach Let F be thermodynamic potential related to Z. Particle, heat reservoir Grand potential Suggestion from canonical ensemble :

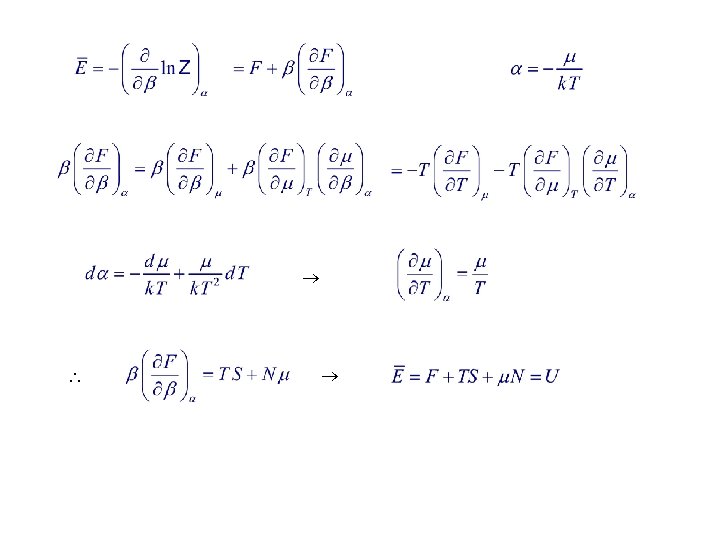
See Reichl, § 2. F. 5. Grand Potential Grand potential : Caution : Prob 4. 2

Using we have

4. 4. Examples Classical Ideal Gas : N ! = Correction for Indistinguishableness Freely moving particles

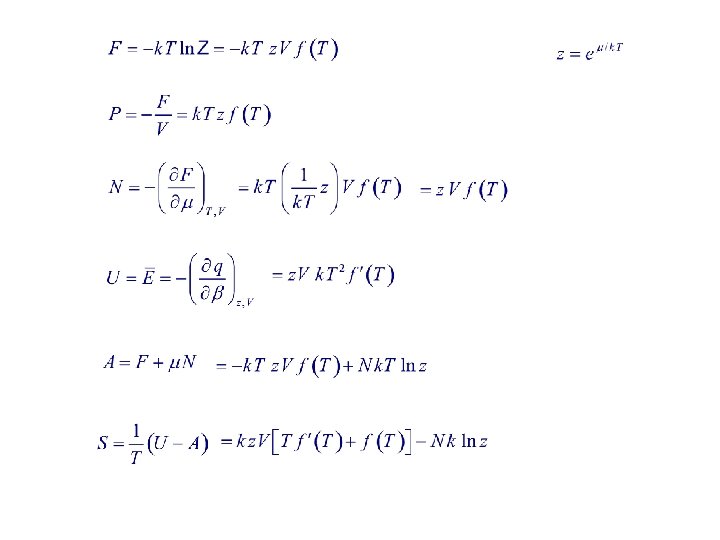
n = 3/2 : nonrelativistic gas. n=3: Find A & S as functions of (T, V, N) yourself. relativistic gas.

Non-Interacting, Localized Particles (distinguishable particles : model for solid ) : Particles localized for or

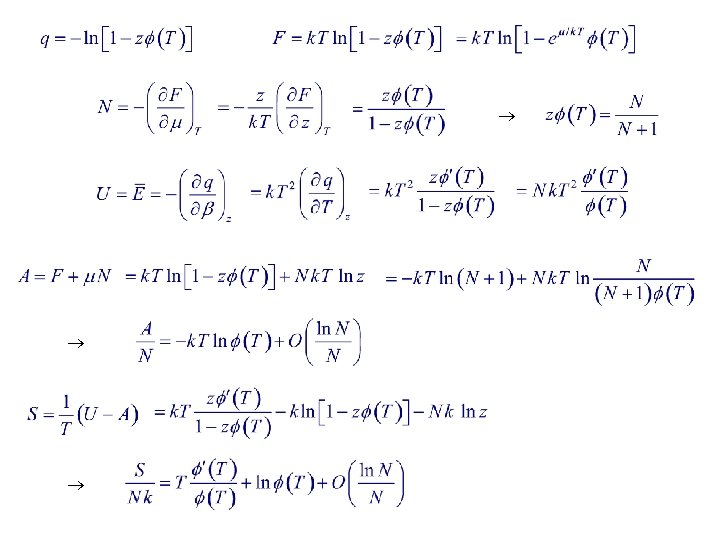
See § 3. 8 Quantum 1 -D oscillators: Classical limit : Consider a substance in vapor-solid phase equilibrium inside a closed vessel. Phase equilibrium i. e. ,

For ideal gas vapor : If For a monatomic gas : From § 3. 5 Einstein model : solid ~ 3 -D oscillators of same

( e / k. T added by hand to account for the difference between binding energies of the solid & gas phases. ) At phase equilibrium: Pure vapor : Tc = characteristic T Solid phase appears : or Since f / e / k. T increases with T , this means Mathematica

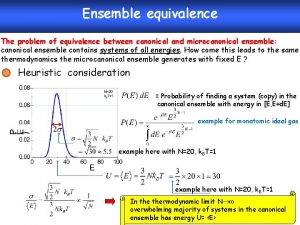
4. 5. Density & Energy Fluctuations in the Grand Canonical Ensemble: Correspondence with Other Ensembles with In general see § 3. 6

Particle density : Particle volume : 1 st law : Euler’ s equation : T = isothermal compressibility

Relative root mean square of n ~0 in thermodynamic limit for finite T At phase transition : , = critical exponents d = dimension of system Experiment on liquid-vapor transition : root mean square of n critical opalescence Grand canonical ensemble

Energy Fluctuations Caution : N = N( P, T )

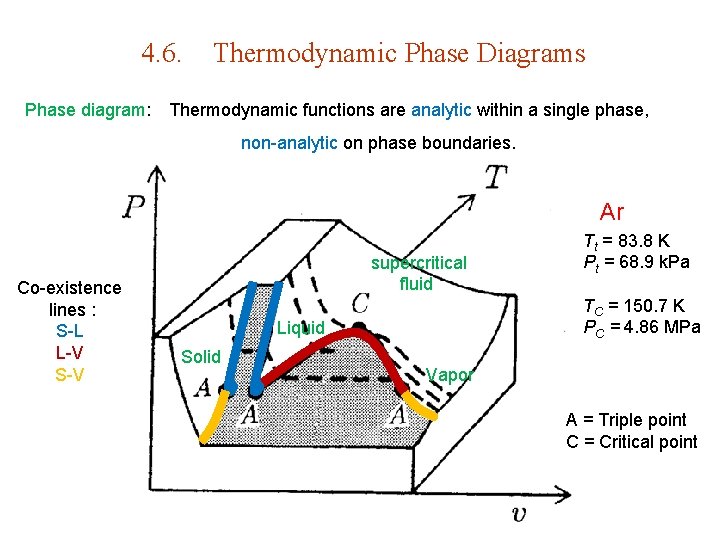
4. 6. Thermodynamic Phase Diagrams Phase diagram: Thermodynamic functions are analytic within a single phase, non-analytic on phase boundaries. Ar Co-existence lines : S-L L-V S-V supercritical fluid TC = 150. 7 K PC = 4. 86 MPa Liquid Solid Tt = 83. 8 K Pt = 68. 9 k. Pa Vapor A = Triple point C = Critical point

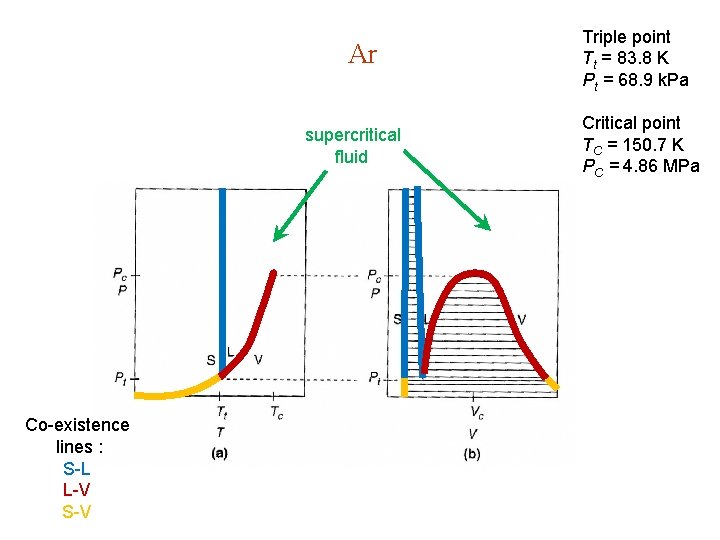
Ar supercritical fluid Co-existence lines : S-L L-V S-V Triple point Tt = 83. 8 K Pt = 68. 9 k. Pa Critical point TC = 150. 7 K PC = 4. 86 MPa

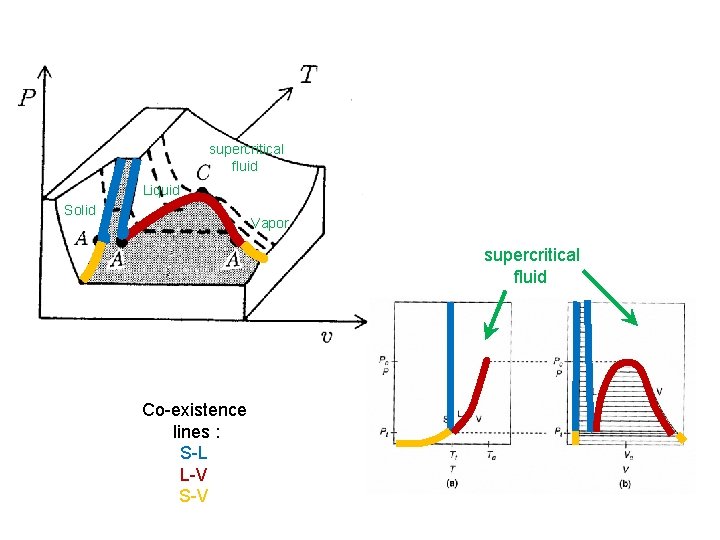
supercritical fluid Liquid Solid Vapor supercritical fluid Co-existence lines : S-L L-V S-V

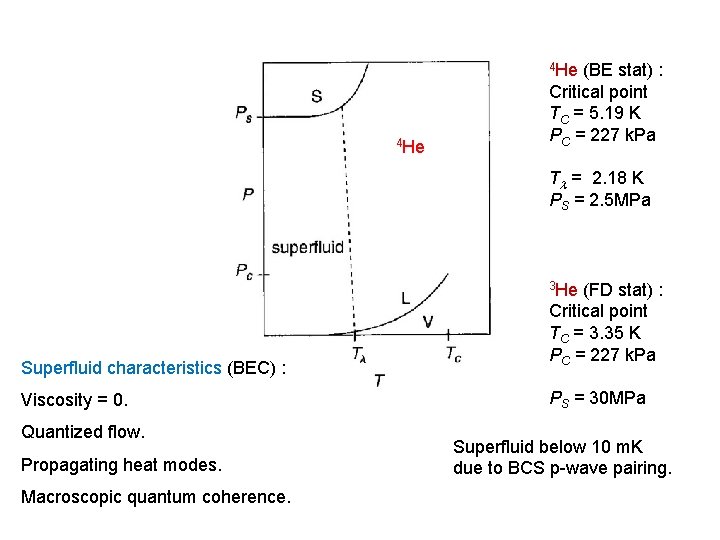
4 He (BE stat) : Critical point TC = 5. 19 K PC = 227 k. Pa T = 2. 18 K PS = 2. 5 MPa 3 He Superfluid characteristics (BEC) : Viscosity = 0. Quantized flow. Propagating heat modes. Macroscopic quantum coherence. (FD stat) : Critical point TC = 3. 35 K PC = 227 k. Pa PS = 30 MPa Superfluid below 10 m. K due to BCS p-wave pairing.

4. 7. Phase Equilibrium & the Clausius-Clapeyron Equation Gibbs free energy = ( P, T ) = chemical potential Consider vessel containing N molecules at constant T & P. Let there be 2 phases initially: vapor (A) & liquid (B). For a given T & P : See Reichl § 2. F At equilibrium, G is a minimum for spontaneous changes

T, P fixed for spontaneous changes At coexistence so that NA can assume any value between 0 & N. Actual NA assumed is determined by U ( via latent heat of vaporization ). Coexistence curve in P-T plane is given by where

Clausius-Clapeyron eq. ( for 1 st order transitions ) Latent heat per particle. Prob. 4. 11, 4. 14 -6. At triple point Slopes are related since Prob. 4. 17.