4 Solusi Persamaan Non Linier Metode Tertutup Metode

4. Solusi Persamaan Non Linier Metode Tertutup & Metode Terbuka 1

Rumusan Masalah l l 2 Mencari solusi persamaan nonlinier Menemukan akar-akar persamaan : f(x) = 0

Metode Pencarian Akar l Metode Tertutup – – l Metode Terbuka – – – 3 Diberikan selang yang sudah diketahui memiliki akar Iterasi yang dilakukan dalam selang ini dipastikan konvergen menuju akar Diperlukan tebakkan awal akar untuk memulai iterasi pencarian akar Hasil suatu hampiran akar akan digunakan untuk mencari hampiran selanjutnya Tebakkan awal akar yang tidak baik dapat menyebabkan iterasinya divergen

Metode Tertutup (Brackecting Methode) l 4 Strategi yang dipakai adalah : mengurangi lebar selang secara sistematis sehingga dengan selang yang menyempit akan mendekatkan pada akar sejati.

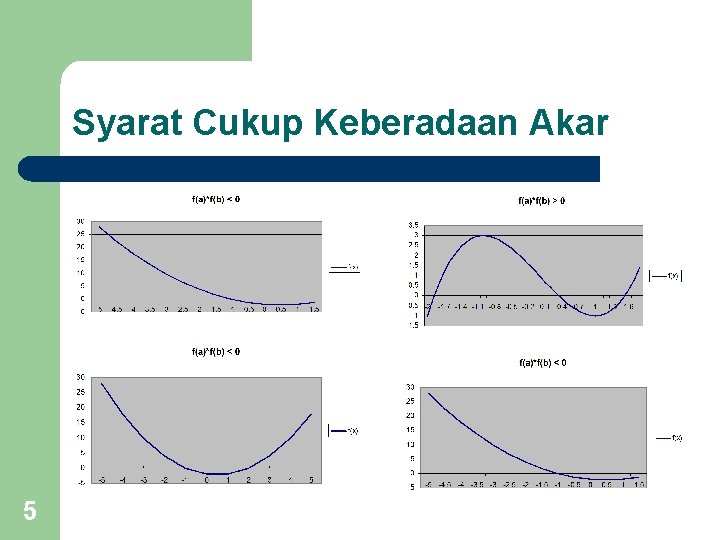
Syarat Cukup Keberadaan Akar 5

Syarat Cukup Keberadaan Akar (Cont. ) l l Jika f(a)*f(b)< 0 dan f(x) kontinu dalam selang [a, b], maka paling sedikit terdapat satu buah akar persamaan f(x) = 0 di dalam selang [a, b] Yang termasuk dalam metode tertutup : – – 6 Metode Bisection (Bagi Dua) Metode Regula False

Konsep Metode Bisection l l l 7 Membagi dua sama besar suatu selang yang diketahui mengandung akar Memilih salah satu selang yang mengandung akar Mengulangi dua hal di atas sampai lebar selang mencapai batas tertentu

Prosedur Metode Bisection 8 Procedure bagidua (a, b : real; var c : real); Const epsilon = 0. 000001; epsilon_mesin = …. ; Begin repeat c = (a+b)/2; if abs(f(c) ) < epsilon_mesin then begin a : = c; b : = c end else if f(a)*f(c) <0 then b : = c { selang baru [a, b] = [a, c]} else a : = c; { selang baru [a, b] =[c, b]} until abs(a-b) < epsilon; End

Kasus yang mungkin l Jumlah akar lebih dari satu l Akar Kembar – l Metode ini tidak bisa menemukan akar ganda Singularitas – – – 9 Hanya satu akar saja yang dapat ditemukan Titik singular, titik yang nilai fungsinya tidak terdefinisi Menyebabkan iterasi yang tidak bisa berhenti Cara memeriksa jika |f(a) – f(b)| menuju ke nol, berarti mendekati nilai sejati.

l Teorema : Jika f(x) kontinu di dalam selang [a, b] dengan f(a)f(b)<0 dan s elemen [a, b] sehingga f(s) = 0 dan cr = (ar+br)/2, maka selalu berlaku : i) ii) 10 | s - cr | < | br – ar | /2 dan | s – cr | < | b – a | / 2 r+1 , r = 0, 1, 2, …

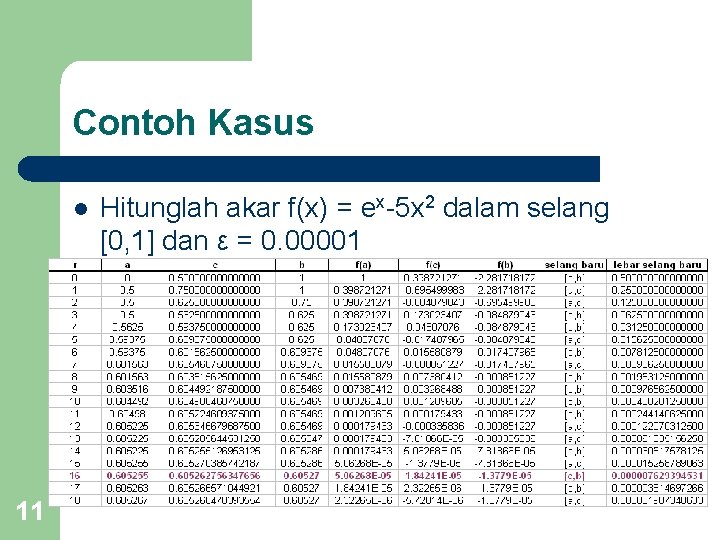
Contoh Kasus l 11 Hitunglah akar f(x) = ex-5 x 2 dalam selang [0, 1] dan ε = 0. 00001

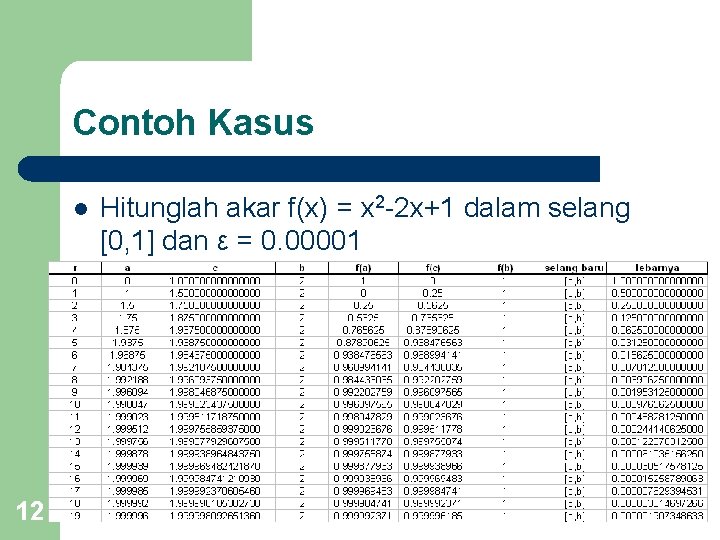
Contoh Kasus l 12 Hitunglah akar f(x) = x 2 -2 x+1 dalam selang [0, 1] dan ε = 0. 00001

Contoh Kasus l 13 Hitunglah akar f(x) = x 3 -4 x 2 -10 dalam selang [1, 2] dan ε = 0. 00001

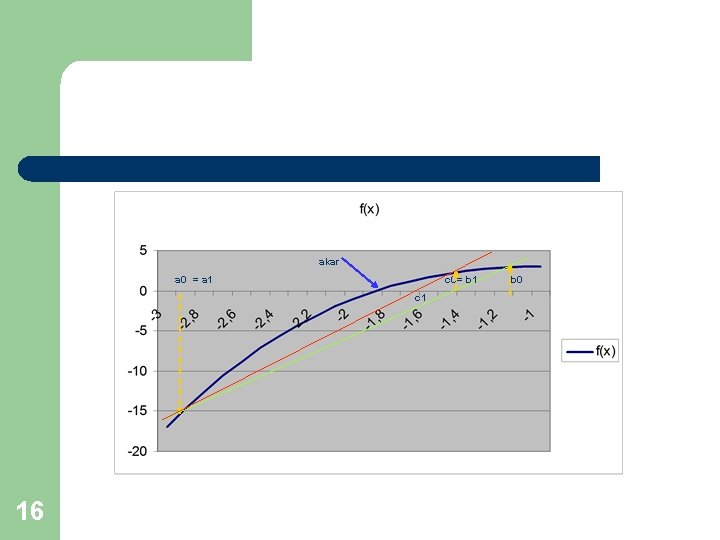
Metode Regula False l l l 14 Mempercepat konvergensi dengan melibatkan nilai f(a) dan nilai f(b) Dibuat garis lurus yang menghubungkan titik (a, f(a)) dengan (b, f(b)). Perpotongan garis tersebut dengan sumbu x menghasilkan hampiran akar.

l 15 Gradien AB = gradien BC

akar a 0 = a 1 c 0= b 1 c 1 16 b 0

Prosedur Metode Regula False 17 Procedure regula false (a, b : real; var c : real); Const epsilon = 0. 000001; epsilon_mesin = …. ; Begin repeat c = b – (f(b)*(b-a)/(f(b)-f(a))); if abs(f(c) ) < epsilon_mesin then begin a : = c; b : =c end else if f(a)*f(c) <0 then b : = c { selang baru [a, b] = [a, c]} else a : = c; { selang baru [a, b] =[c, b]} until abs(a-b) < epsilon; End

Contoh Kasus l 18 Hitunglah akar f(x) = ex-5 x 2 dalam selang [0, 1] dan ε = 0. 00001

Metode Terbuka l l l 19 Metode Iterasi Titik Tetap Metode Newton Metode Secant

Metode Iterasi Titik Tetap l l l 20 Bentuk persamaan x = g(x) dari persamaan f(x) = 0. Buat prosedur iterasi xr+1 = g(xr) Berilah suatu nilai tebakan akar Hitung hampiran akar per iterasi Mendapatkan akar sejati s, jika f(s) = 0 atau s = g(s). Kondisi berhenti |xr+1 – xr| < ε atau |(xr+1 – xr)/xr+1| < δ dengan ε dan δ sudah ditetapkan nilainya

Prosedur Iterasi Titik Tetap Procedure iterasi_titik_tetap( var x : real); Const epsilon = 0. 000001; var x_prev : real; function g(x: real): real; Begin repeat x_prev : = x; x : = g(x); until abs(x – x_prev) < epsilon End 21

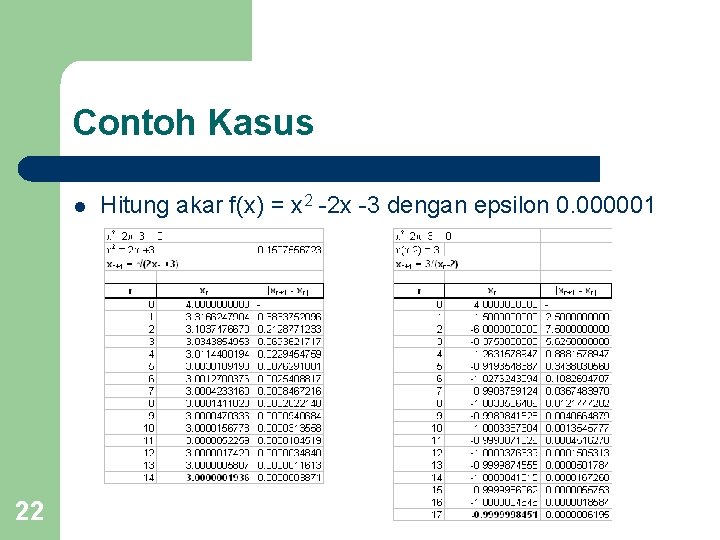
Contoh Kasus l 22 Hitung akar f(x) = x 2 -2 x -3 dengan epsilon 0. 000001

23

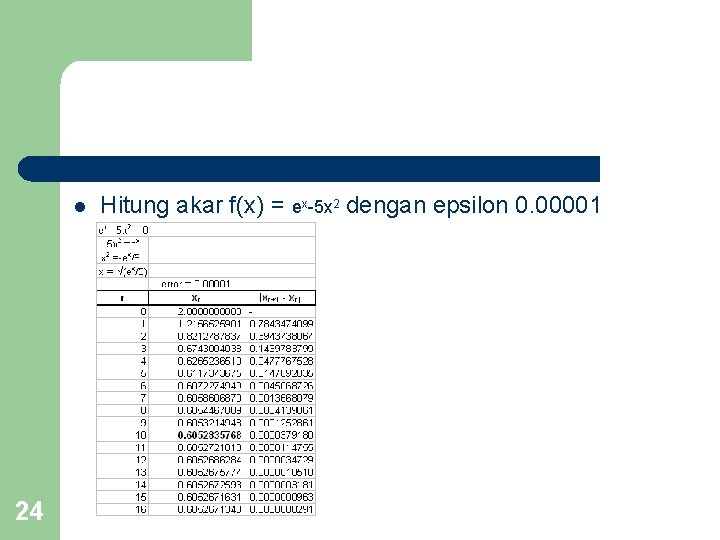
l 24 Hitung akar f(x) = ex-5 x 2 dengan epsilon 0. 00001

Kriteria Konvergensi l Teorema : Misalkan g(x) dan g’(x) kontinu dalam selang [a, b] = [s-h, s+h] yang mengandung titik tetap s dan nilai awal x 0 dipilih dalam selang tersebut. Jika |g’(x)|<1 untuk semua x elemen [a, b] maka iterasi xr+1 = g(xr) akan konvergen ke s. Pada kasus ini s disebut juga titik atraktif Jika |g’(x)|>1 untuk semua x elemen [a, b] maka iterasi xr+1 = g(xr) akan divergen dari s 25

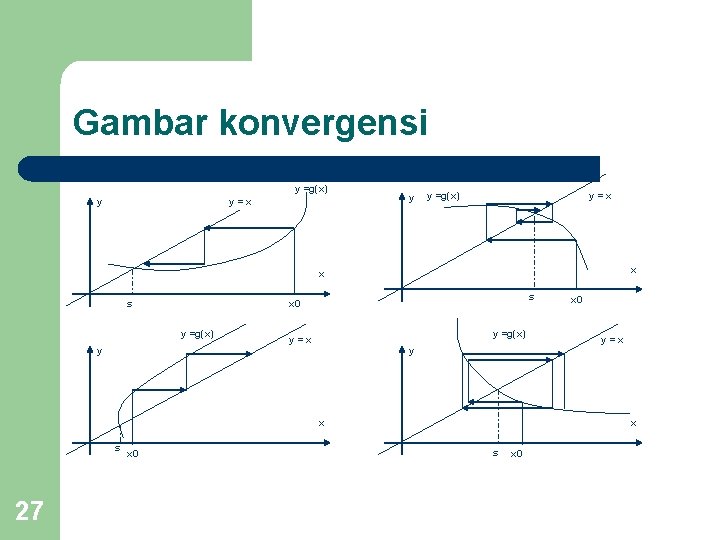
Kriteria Konvergensi (Cont. ) Resume : Dalam selang I = [s-h, s+h] dengan s titik tetap l Jika 0<g’(x)<1 untuk setiap x elemen I Iterasi konvergen monoton Jika -1<g’(x)<0 untuk setiap x elemen I Iterasi konvergen berosilasi Jika g’(x)>1 untuk setiap x elemen I Iterasi divergen monoton Jika g’(x)<-1 untuk setiap x elemen I Iterasi divergen berosilasi 26

Gambar konvergensi y =g(x) y y=x y y =g(x) y=x x x s y =g(x) y s x 0 y =g(x) y=x y x s 27 x 0 y=x x s x 0

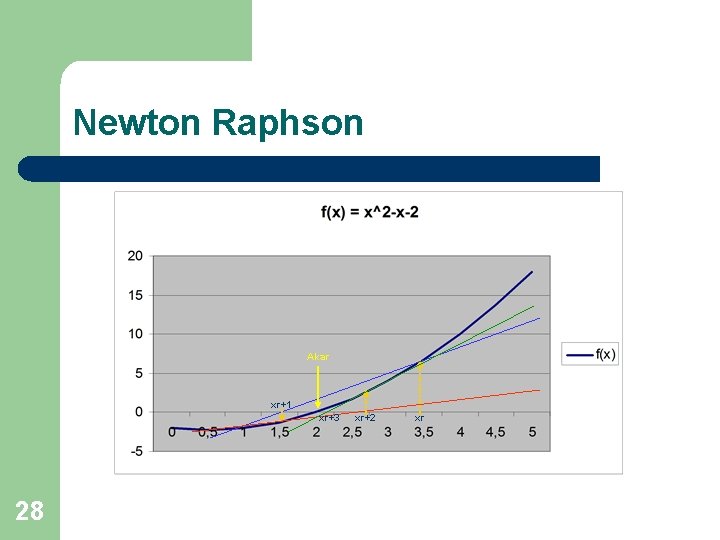
Newton Raphson Akar xr+1 xr+3 28 xr+2 xr

Metode Newton Raphson l l l 29 Prosedur pencarian akar mirip dengan iterasi titik tetap Prosedur iterasi yang digunakan didapatkan melalui suatu penurunan rumus : xr+1 = xr – f(xr)/f’(xr) Kondisi berhenti yang digunakan sama dengan pada iterasi titik tetap

Prosedur Newton Raphson Procedure newton_raphson( var x : real); Const epsilon = 0. 000001; var x_prev : real; function f(x: real): real; function f_turunan(x: real): real; Begin repeat x_prev : = x; x : = x –f(x)/f_turunan(x); until abs(x – x_prev) < epsilon End 30

NR untuk menghitung akar ? l l 31 Bagaimana mencari √c ? Bagaimana menghitung 1/c ?

Konvergensi Metode NR l 32 Untuk tebakkan akar x, nilai |f(x)f’’(x)/(f’(x)) 2|<1, dimana f’(x) <> 0

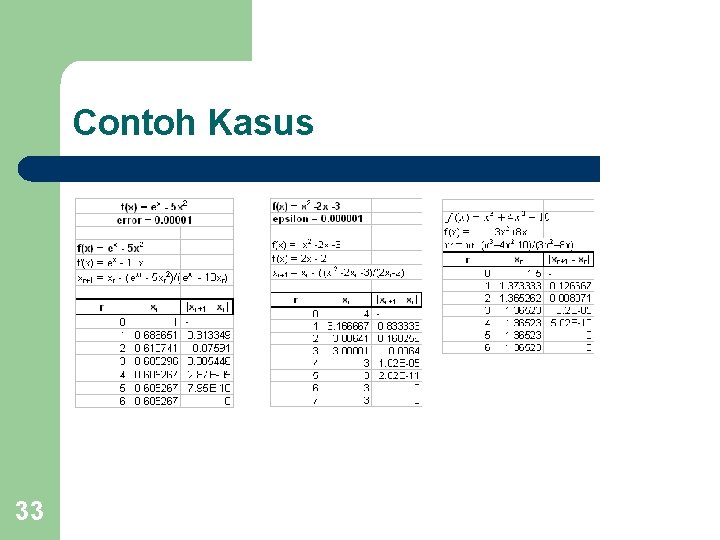
Contoh Kasus 33

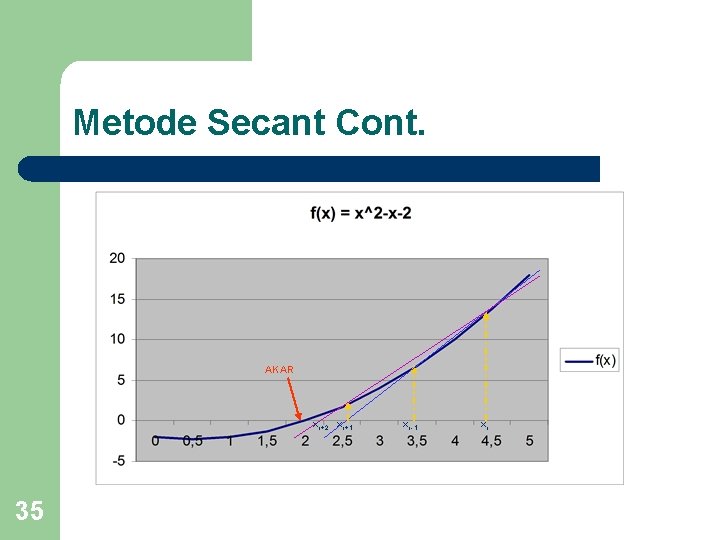
Metode Secant l l 34 Tidak semua fungsi dapat dihitung dengan mudah turunannya. Merupakan modifikasi metode NR Prosedur iterasinya menjadi : xr +1 = xr – (f(xr)(xr-xr-1)/(f(xr)-f(xr-1))) Kondisi berhenti menggunakan ketentuan yang sama dengan NR

Metode Secant Cont. AKAR xr+2 xr+1 35 xr-1 xr

Procedure Metode Secant Procedure secant( x 0, x 1 : real; var x : real); Const epsilon = 0. 000001; var x_prev : real; function f(x: real): real; Begin repeat x_prev : = x 1; x : = x – (f(x)*(x 1 -x 0)/(f(x 1)-f(x 0))); x 0 : = x 1 : = x until abs(x – x_prev) < epsilon End 36

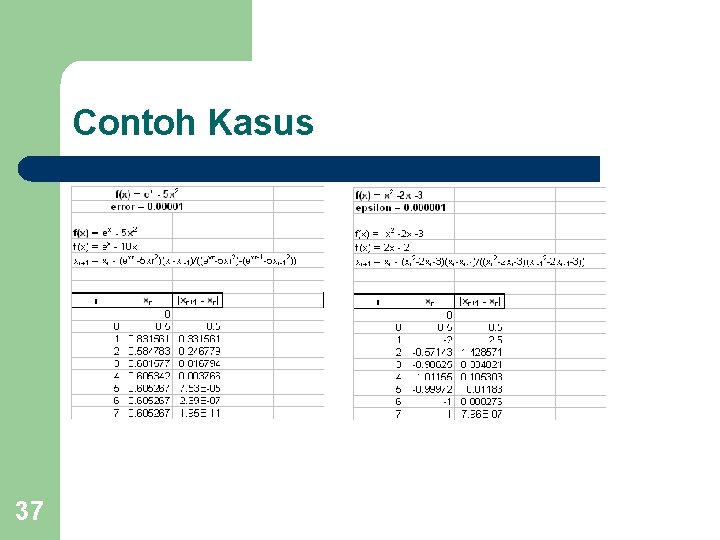
Contoh Kasus 37