4 Perceptron Learning Rule 1 4 Learning Rules

4 Perceptron Learning Rule 1

4 Learning Rules : A procedure for modifying the weights and biases of a net work. Learning Rules : Supervised Learning Reinforcement Learning Unsupervised Learning 2

4 Learning Rules • Supervised Learning Network is provided with a set of examples of proper network behavior (inputs/targets) {p 1, t 1}, {p 2, t 2}, ……{pn, tn} • Reinforcement Learning Network is only provided with a grade, or score, which indicates network performance • Unsupervised Learning Only network inputs are available to the learning algorithm. Network learns to categorize (cluster) the inputs. 3

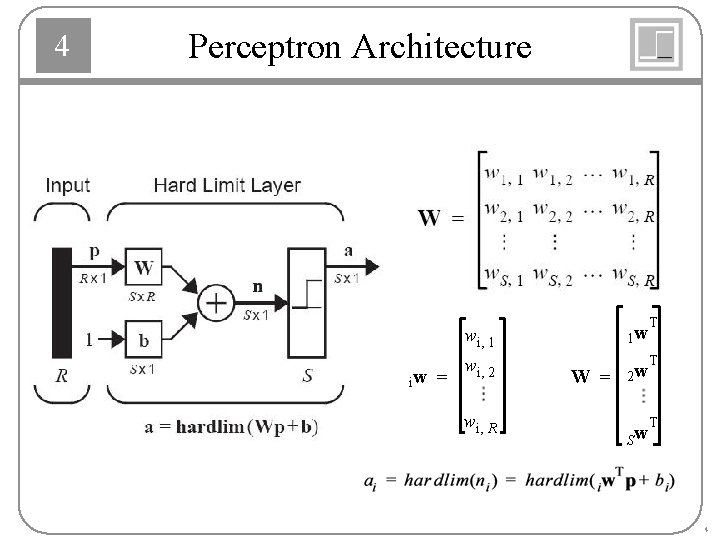
4 Perceptron Architecture iw = T w i, 1 1 w w i, 2 W = 2 w w i, R T T Sw 4

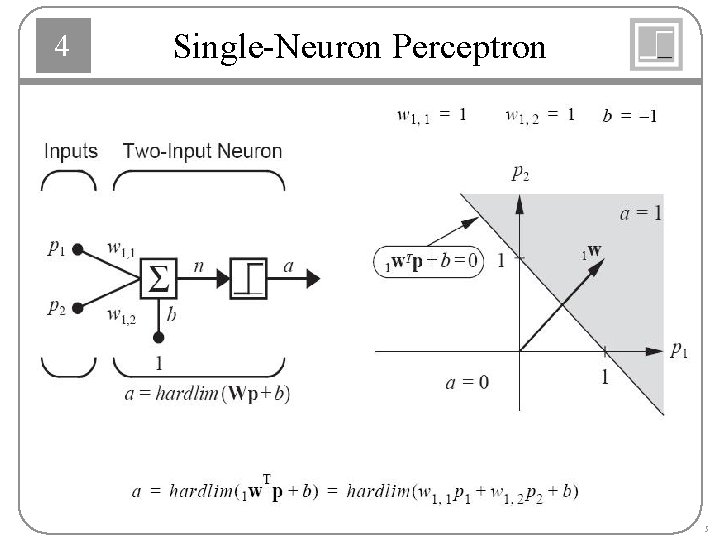
4 Single-Neuron Perceptron 5

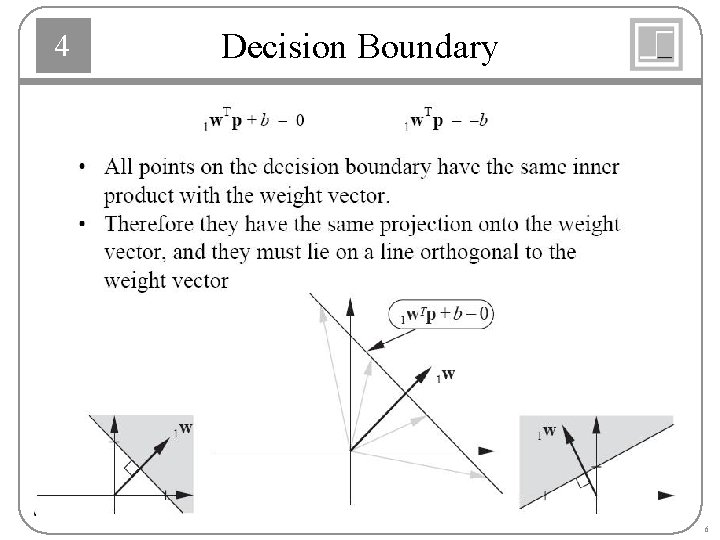
4 Decision Boundary 6

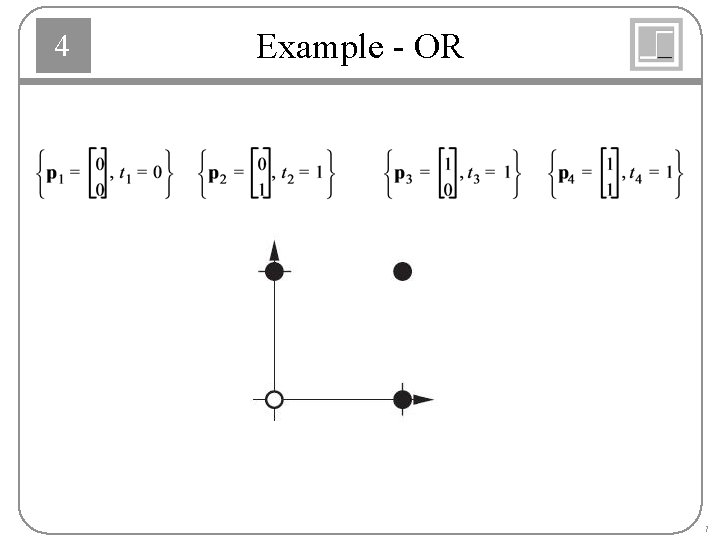
4 Example - OR 7

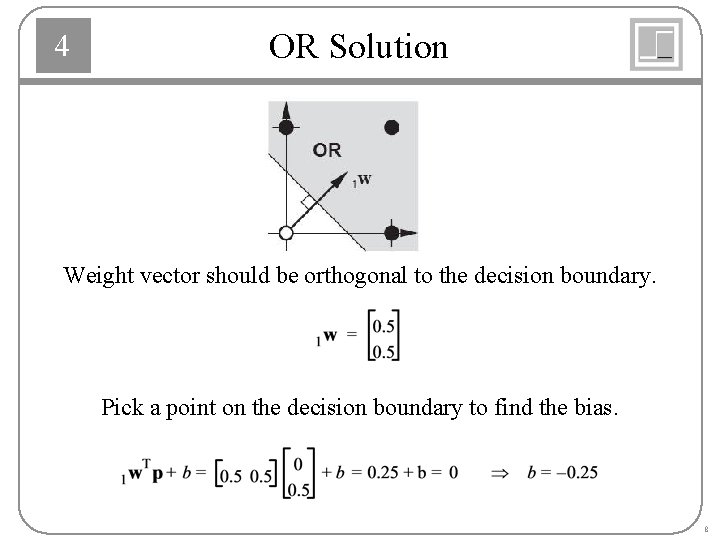
4 OR Solution Weight vector should be orthogonal to the decision boundary. Pick a point on the decision boundary to find the bias. 8

4 Multiple-Neuron Perceptron Each neuron will have its own decision boundary. Tp+b =0 w i i A single neuron can classify input vectors into two categories. A S-neuron perceptron can classify input vectors into 2 S categories. 9

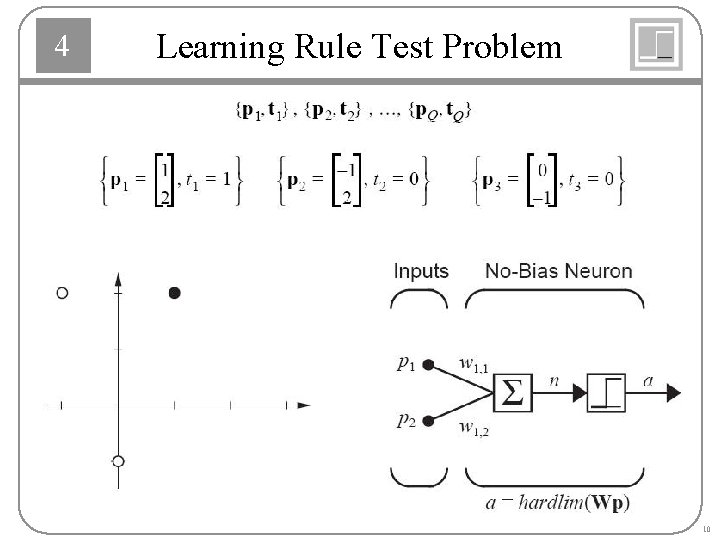
4 Learning Rule Test Problem 10

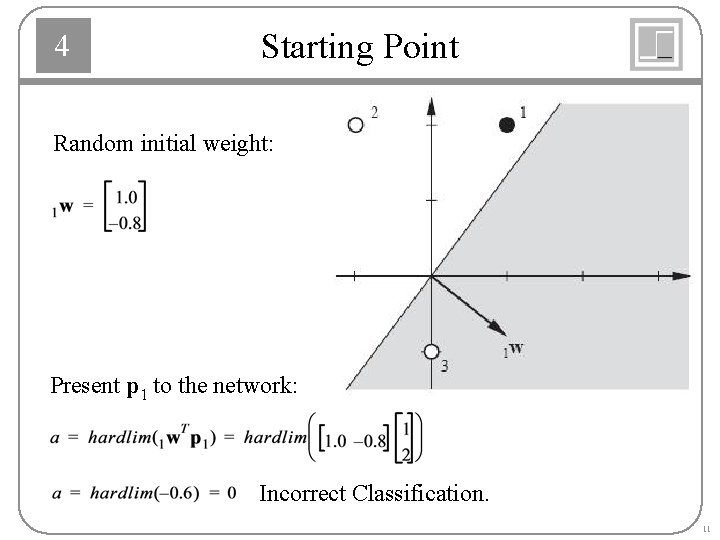
4 Starting Point Random initial weight: Present p 1 to the network: Incorrect Classification. 11

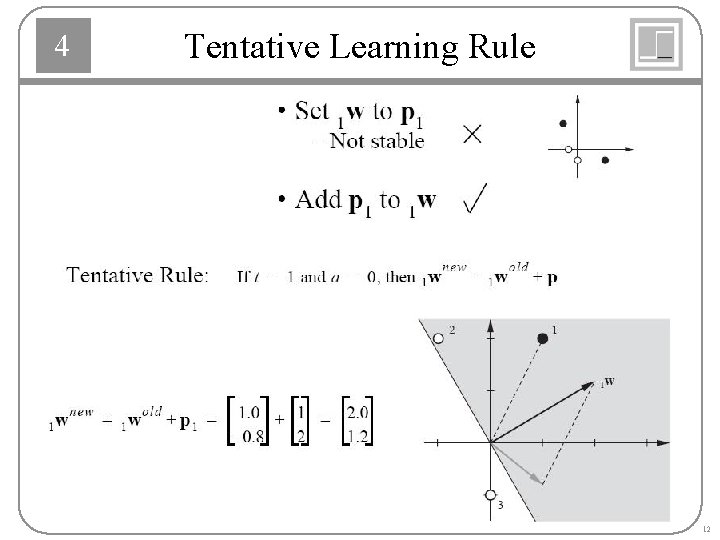
4 Tentative Learning Rule 12

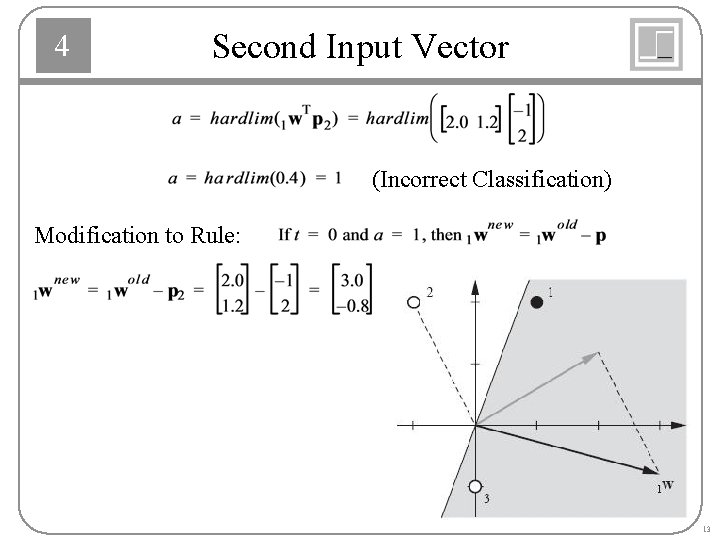
4 Second Input Vector (Incorrect Classification) Modification to Rule: 13

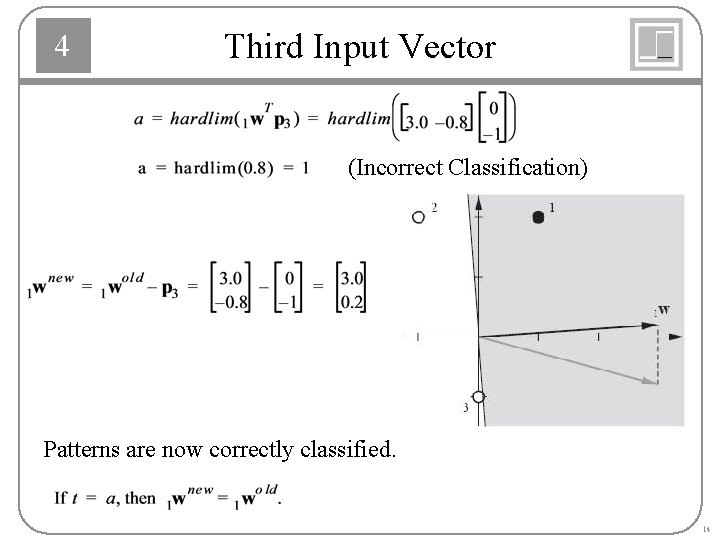
4 Third Input Vector (Incorrect Classification) Patterns are now correctly classified. 14

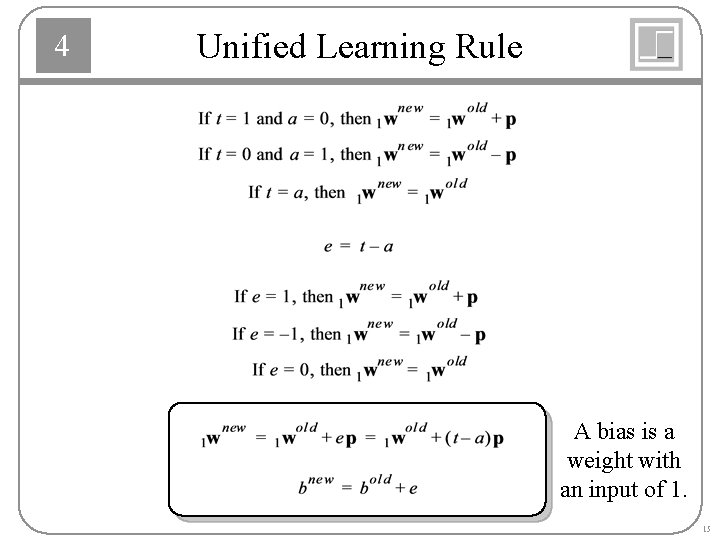
4 Unified Learning Rule A bias is a weight with an input of 1. 15

4 Multiple-Neuron Perceptrons To update the i-th row of the weight matrix: Matrix form: 16

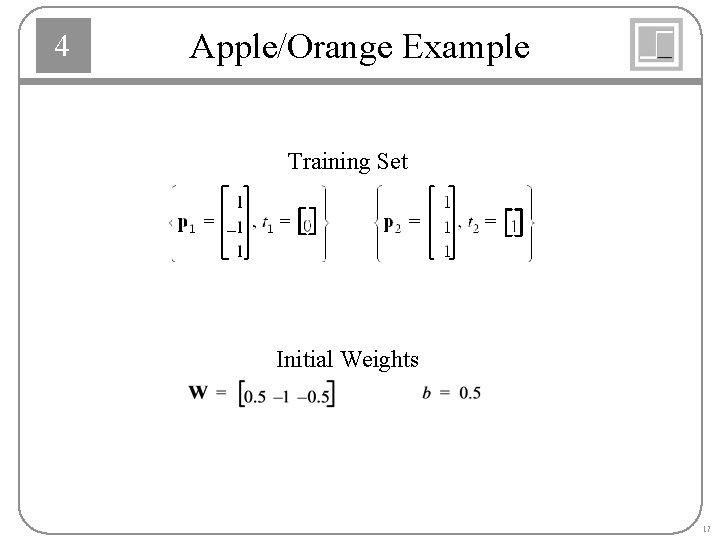
4 Apple/Orange Example Training Set Initial Weights 17

4 Apple/Orange Example First Iteration e = t 1 – a = 0 – 1 = -1 18

4 Second Iteration 19

4 Third Iteration e = t 1 – a = 0 – 1 = -1 20

4 Check a = hardlim(-3. 5) = 0 = t 1 a = hardlim(0. 5) = 1 = t 2 21

4 Perceptron Rule Capability The perceptron rule will always converge to weights which accomplish the desired classification, assuming that such weights exist. 22

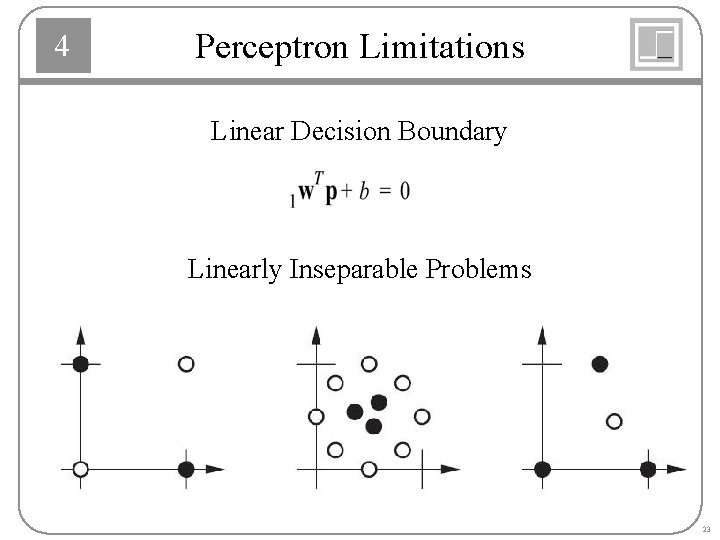
4 Perceptron Limitations Linear Decision Boundary Linearly Inseparable Problems 23

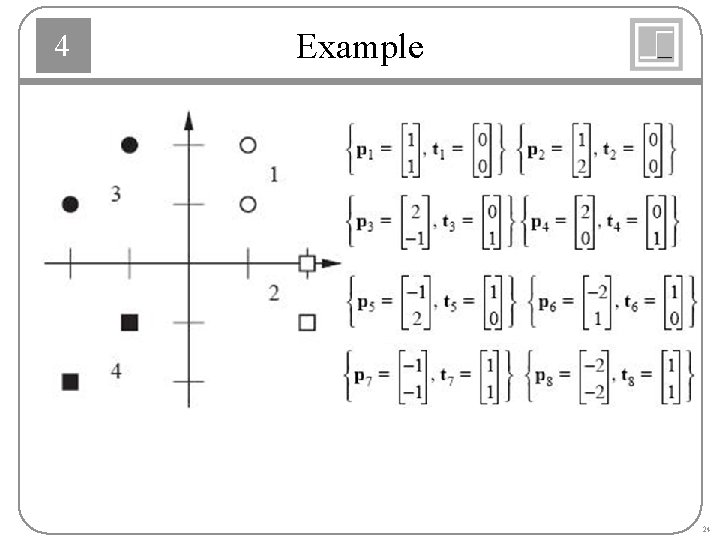
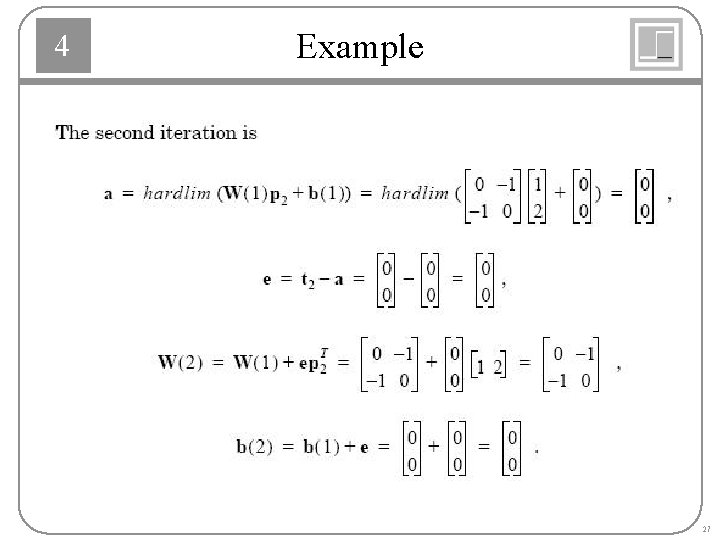
4 Example 24

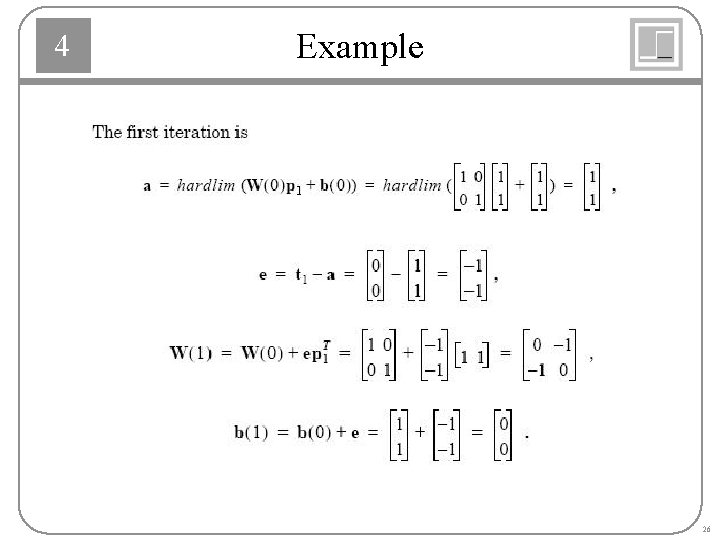
4 Example 25

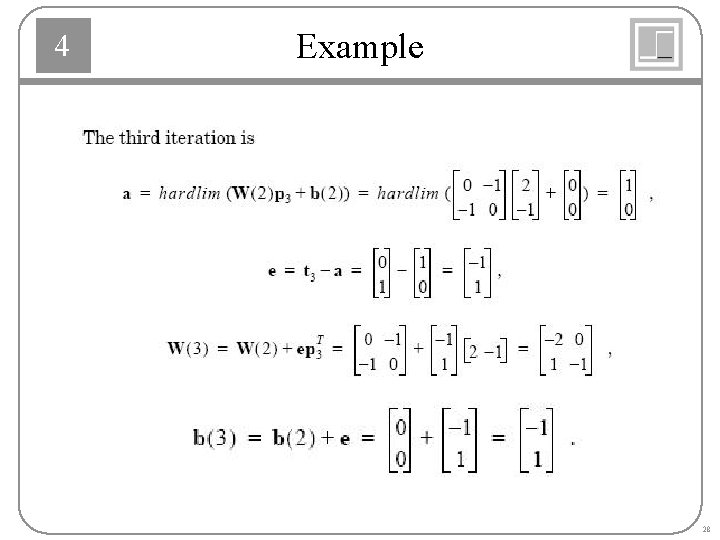
4 Example 26

4 Example 27

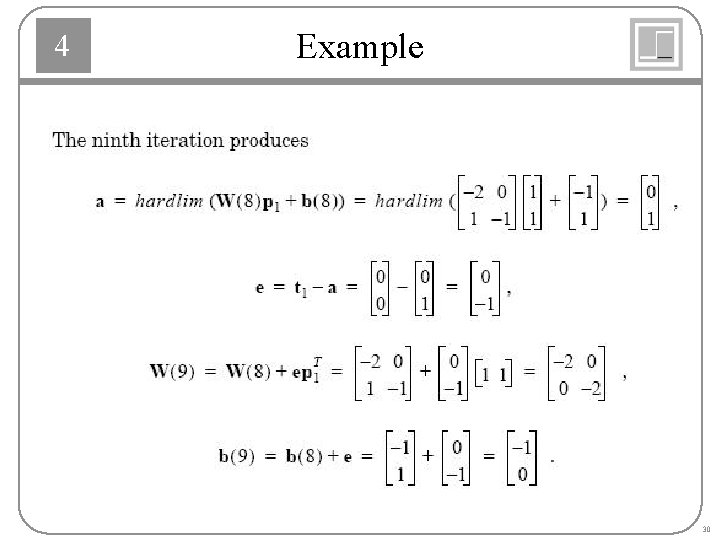
4 Example 28

4 Example 29

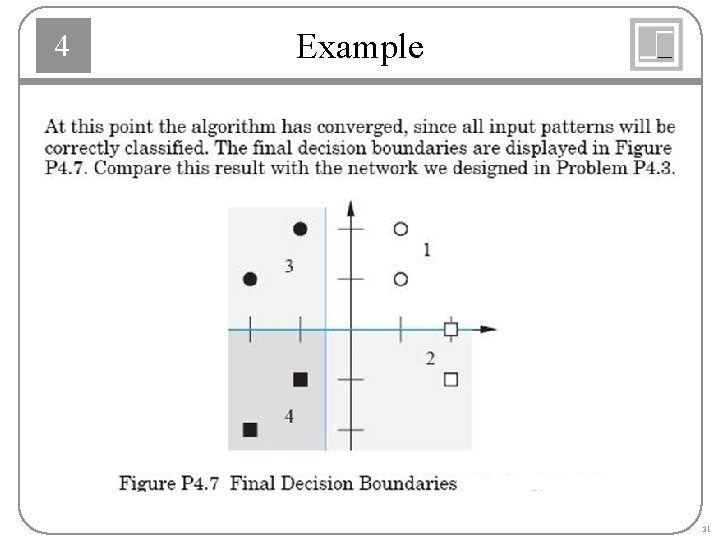
4 Example 30

4 Example 31