4 Perceptron Learning Rule 1 4 Learning Rules

4 Perceptron Learning Rule 1

4 Learning Rules • Supervised Learning Network is provided with a set of examples of proper network behavior (inputs/targets) • Reinforcement Learning Network is only provided with a grade, or score, which indicates network performance • Unsupervised Learning Only network inputs are available to the learning algorithm. Network learns to categorize (cluster) the inputs. 2

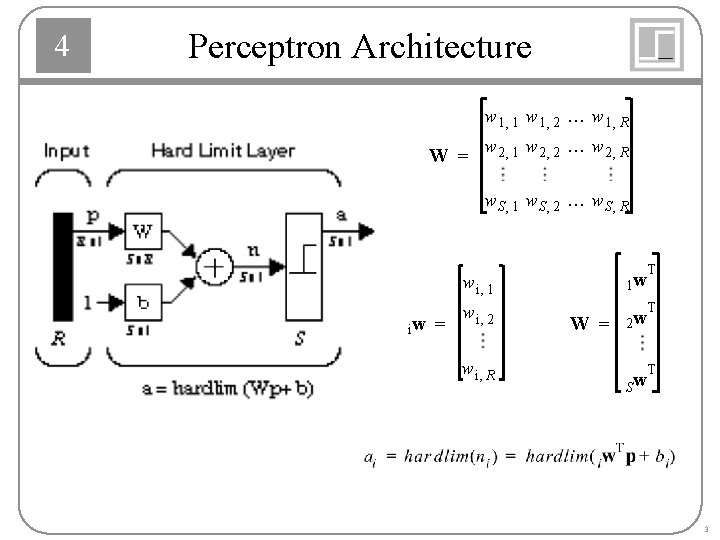
4 Perceptron Architecture w 1, 1 w 1, 2 ¼ w 1, R w w w W = 2, 1 2, 2 ¼ 2, R w S, 1 w S, 2 ¼ w S, R T 1 w w i, 1 iw = w i, 2 w i, R W = T 2 w T Sw 3

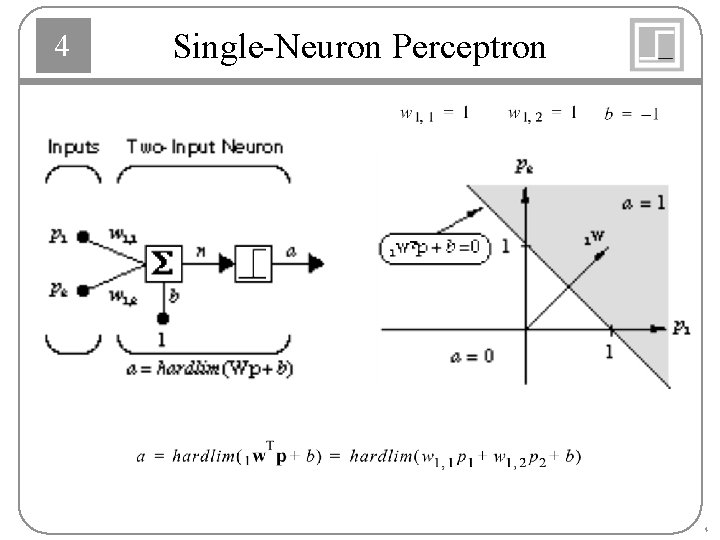
4 Single-Neuron Perceptron 4

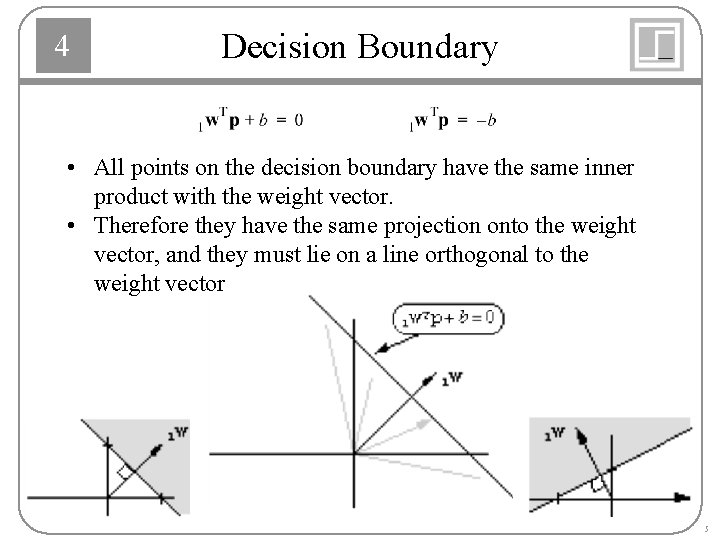
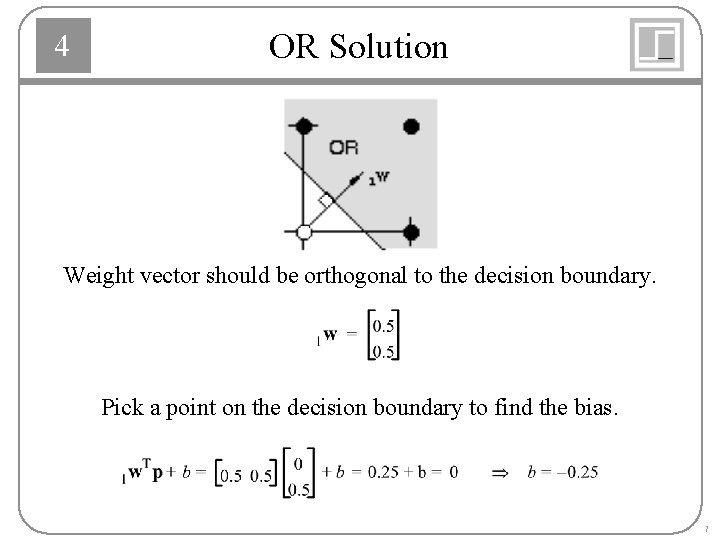
4 Decision Boundary • All points on the decision boundary have the same inner product with the weight vector. • Therefore they have the same projection onto the weight vector, and they must lie on a line orthogonal to the weight vector 5

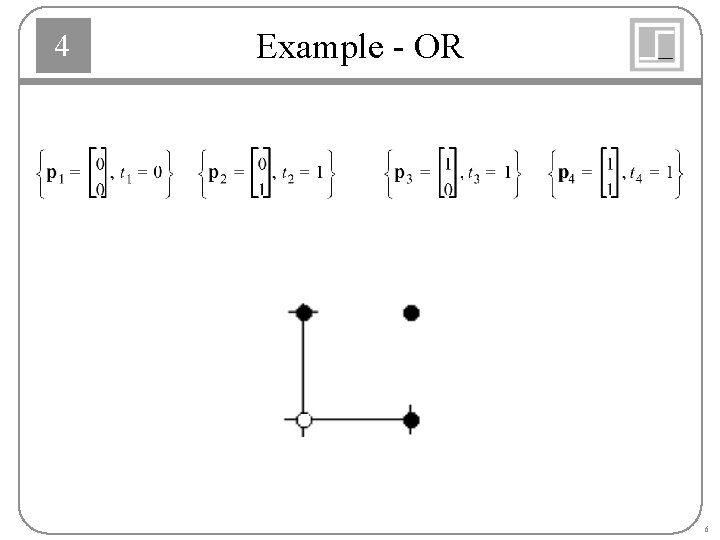
4 Example - OR 6

4 OR Solution Weight vector should be orthogonal to the decision boundary. Pick a point on the decision boundary to find the bias. 7

4 Multiple-Neuron Perceptron Each neuron will have its own decision boundary. A single neuron can classify input vectors into two categories. A multi-neuron perceptron can classify input vectors into 2 S categories. 8

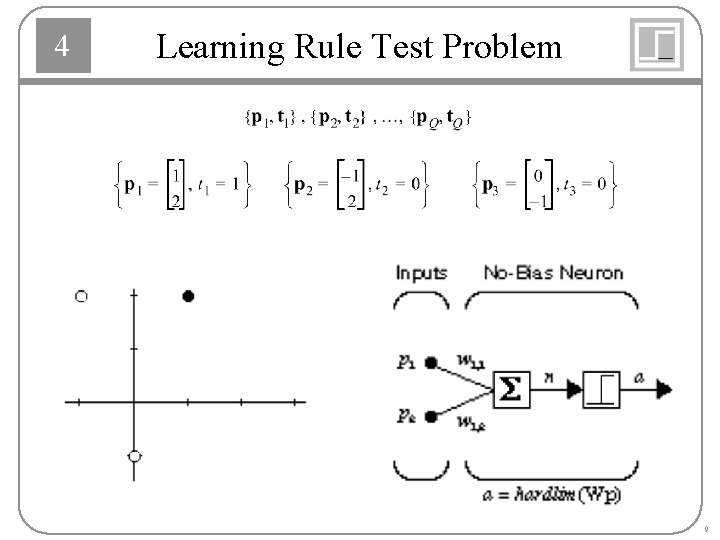
4 Learning Rule Test Problem 9

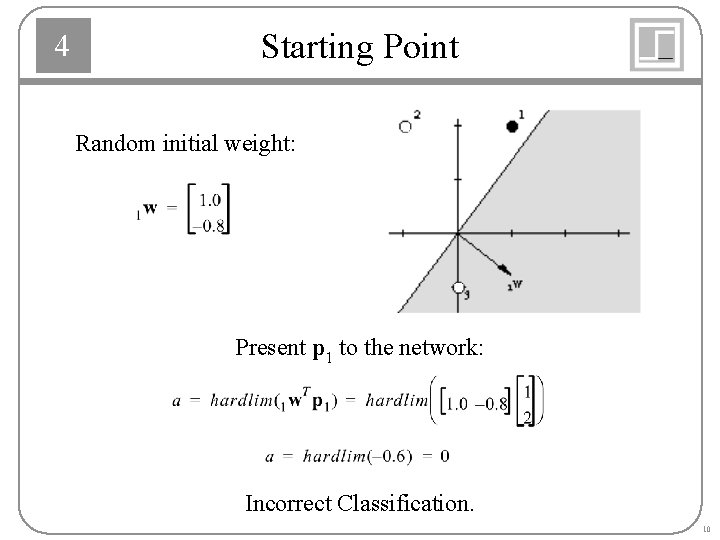
4 Starting Point Random initial weight: Present p 1 to the network: Incorrect Classification. 10

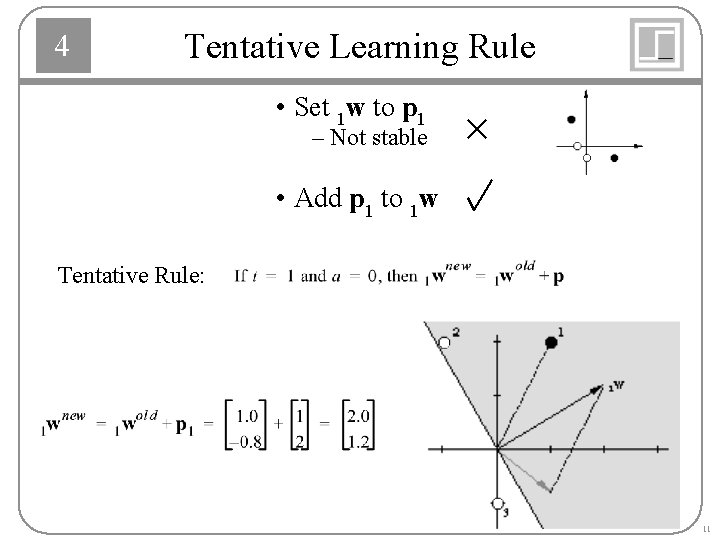
4 Tentative Learning Rule • Set 1 w to p 1 – Not stable • Add p 1 to 1 w Tentative Rule: 11

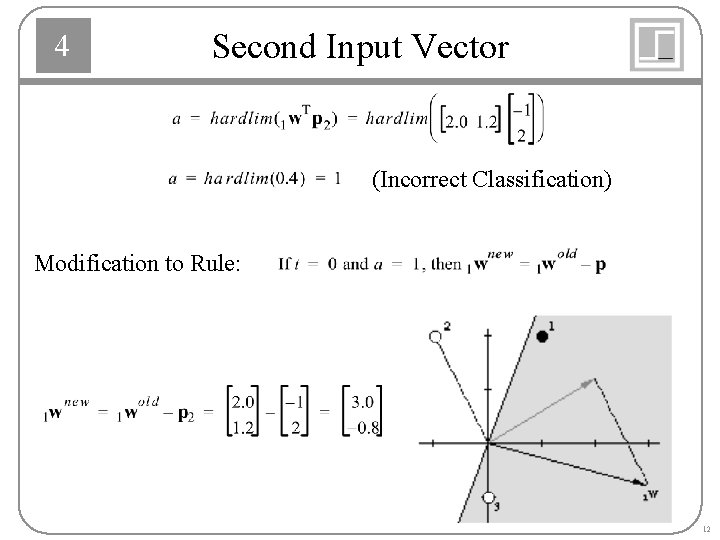
4 Second Input Vector (Incorrect Classification) Modification to Rule: 12

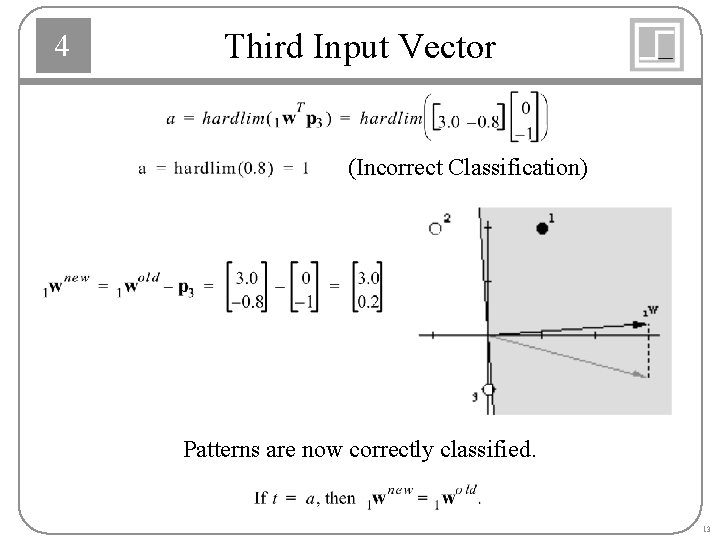
4 Third Input Vector (Incorrect Classification) Patterns are now correctly classified. 13

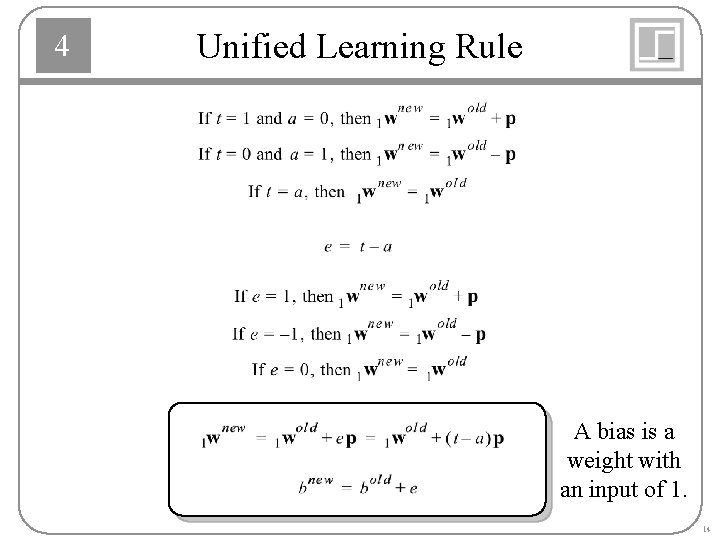
4 Unified Learning Rule A bias is a weight with an input of 1. 14

4 Multiple-Neuron Perceptrons To update the ith row of the weight matrix: Matrix form: 15

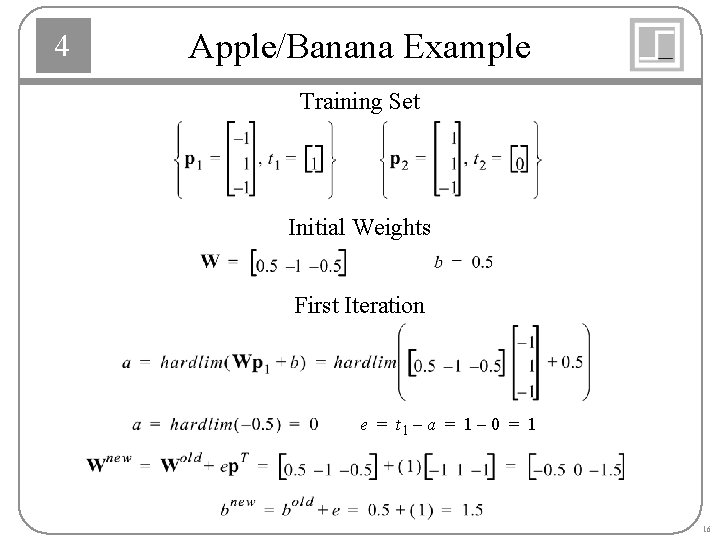
4 Apple/Banana Example Training Set Initial Weights First Iteration e = t 1 – a = 1 – 0 = 1 16

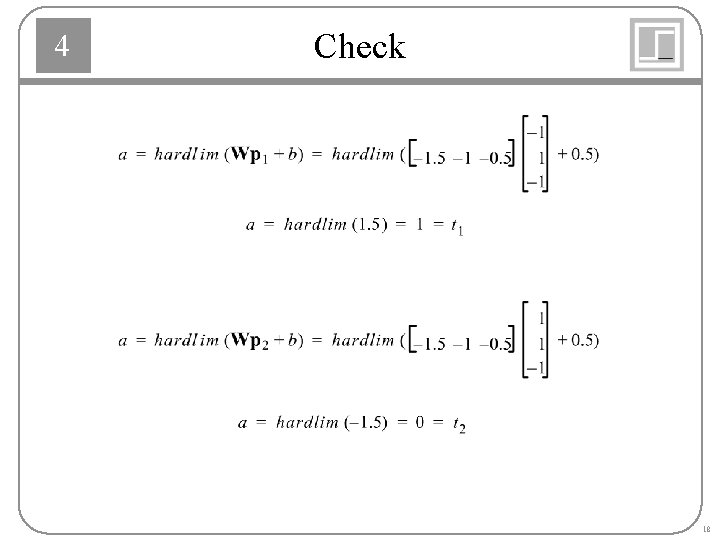
4 Second Iteration 17

4 Check 18

4 Perceptron Rule Capability The perceptron rule will always converge to weights which accomplish the desired classification, assuming that such weights exist. 19

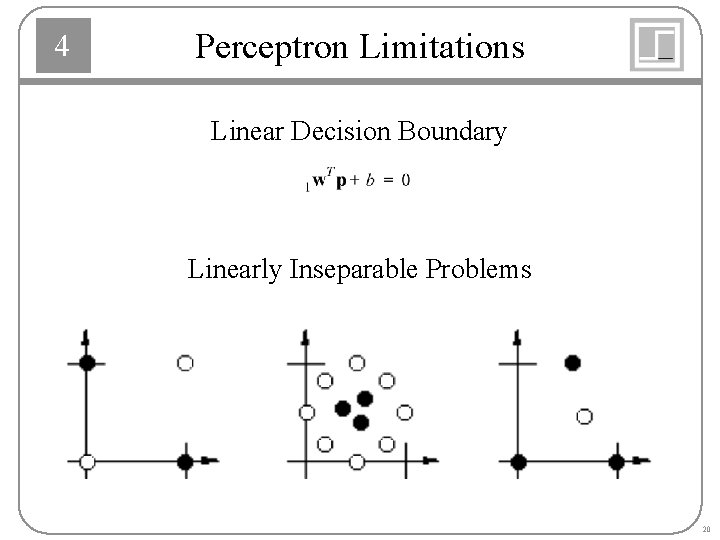
4 Perceptron Limitations Linear Decision Boundary Linearly Inseparable Problems 20