4 Notes METRIC AND MEASUREMENTS Basic Math Tools

#4 Notes : METRIC AND MEASUREMENTS/ Basic Math Tools w. Scientific Notation w. Significant Digits w. Metric System w. Dimensional Analysis

FOCUSED LEARNING TARGET In Analyzing data, I will be able to define, explain, interpret the observed measurements through the exploration of Science and Engineering Practices such as the use of : Scientific Notation Significant Figures Rules of Rounding off of Numbers Measurements Dimensional Analysis

SCIENTIFIC NOTATION Makes very large or small numbers easy to use Two parts: 1 x < 10 (including 1 but NOT 10) x 10 exponent

WRITING SCIENTIFIC NOTATION EXAMPLES: 1) 2) 3) 4) 5) 6) 2, 000, 000 5430 0. 000000123 0. 007872 966, 666, 000 0. 0000600 = = = 2 X 10 9 5. 43 X 10 3 1. 23 X 10 -7 7. 872 X 10 -3 9. 66666 X 10 6. 00 X 10 -5 8 LARGE NUMBERS (>1) POSITIVE EXPONENTS EQUAL TO 1 or itself ZERO EXPONENTS SMALL NUMBERS (<1) NEGATIVE EXPONENTS

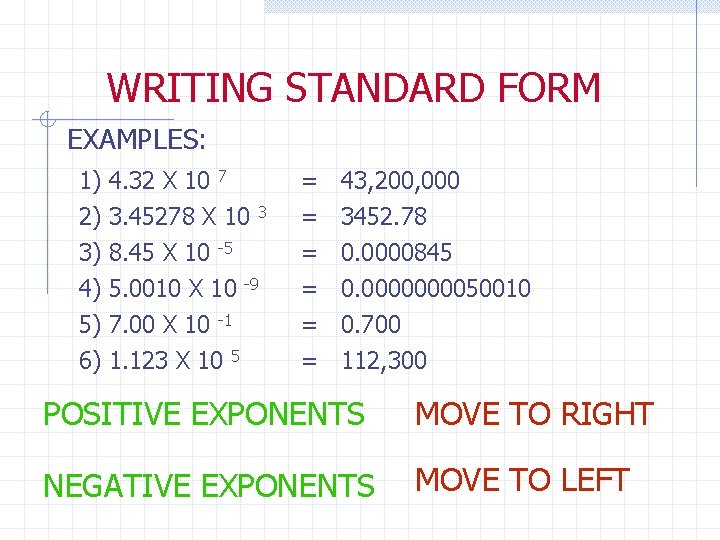
WRITING STANDARD FORM EXAMPLES: 1) 2) 3) 4) 5) 6) 4. 32 X 10 7 3. 45278 X 10 3 8. 45 X 10 -5 5. 0010 X 10 -9 7. 00 X 10 -1 1. 123 X 10 5 = = = 43, 200, 000 3452. 78 0. 0000845 0. 000050010 0. 700 112, 300 POSITIVE EXPONENTS MOVE TO RIGHT NEGATIVE EXPONENTS MOVE TO LEFT

SIGNIFICANT DIGITS Exact numbers are without uncertainty and error Measured numbers are measured using instruments and have some degree of uncertainty and error Degree of accuracy of measured quantity depends on the measuring instrument

RULES 1) All NONZERO digits are significant Examples: a) 543, 454, 545 b) 34, 000 c) 65, 945 = 9 = 2 = 5 2) Trailing zeros are NOT significant Examples: = 1 a) 1, 000 b) 234, 500 = 4 c) 34, 288, 900, 000 = 6

RULES CON’T 3) Zero’s surrounded by significant digits are significant Examples: a) 1, 000, 330, 134 = 10 b) 534, 001, 000 = 6 c) 7, 001, 000, 100 = 8 4) For scientific notations, all the digits in the first part are significant Examples: a) 1. 000 x 10 9 b) 2. 34 x 10 -16 c) 3. 4900 x 10 23 = 4 = 3 = 5

RULES CON’T 5) Zero’s are significant if a) there is a decimal present (anywhere) b) AND a significant digit in front of the zero Zero’s at beginning of a number are not significant (placement holder) Examples: a) 0. 00100 = 3 e) 0. 0000007 = 1 b) 0. 1001232 = 7 f) 0. 003400 = 4 c) 1. 00100 = 6 g) 0. 0700 = 3 d) 8900. 00000 = 9 h) 0. 040100 = 5

Rules for Rounding in Calculations

Rounding with 5’s: UP n ____ 5 greater than zero 10. 257 = 10. 3 34. 3591 = 34. 4 § ODD 99. 750 101. 15 5 zero = 99. 8 = 101. 2

Rounding with 5’s: DOWN § EVEN 6. 850 101. 25 5 zero = 6. 8 = 101. 2

CALCULATIONS 1) Multiply and Divide: Least number of significant digits Examples: a) 0. 102 x 0. 0821 x 273 b) 0. 1001232 x 0. 14 x 6. 022 x 10 12 c) 0. 500 / 44. 02 d) 8900. 00000 x 4. 031 x 0. 08206 0. 995 e) 150 / 4 f) 4. 0 x 104 x 5. 021 x 10– 3 x 7. 34993 x 102 g) 3. 00 x 10 6 / 4. 00 x 10 -7 = 2. 2861566 = 8. 4412 x 1010 = 0. 011358473 = 2958. 770205 = 37. 5 = 147615. 9941 = 7. 5 x 1012

CALCULATIONS 2) Add and Subtract: Least precise decimal position Examples: a) 212. 2 + 26. 7 + 402. 09 212. 2 26. 7 402. 09 640. 99 = 641. 0 212. 2 26. 7 402. 09 640. 99

ADD AND SUBTRACT CON’T Examples: b) 1. 0028 + 0. 221 + 0. 10337 1. 0028 0. 221 0. 10337 1. 32717 = 1. 327 1. 0028 0. 221 0. 10337 1. 32717

ADD AND SUBTRACT CON’T Examples: c) 102. 01 + 0. 0023 + 0. 15 102. 01 0. 0023 0. 15 102. 1623 = 102. 16

ADD AND SUBTRACT CON’T Examples: d) 1. 000 x 104 - 1 10000 1 9999 = 1. 000 x 104

ADD AND SUBTRACT CON’T Examples: e) 55. 0001 + 0. 0002 + 0. 104 55. 0001 0. 0002 0. 104 55. 1043 = 55. 104

ADD AND SUBTRACT CON’T Examples: f) 1. 02 x 103 + 1. 02 x 102 + 1. 02 x 101 1020 102 10. 2 1132. 2 = 1130 102 10. 2 1132. 2 1020 102 10. 2 1132. 2

MIX PRACTICE Examples: a) 52. 331 + 26. 01 - 0. 9981 = 77. 3429 = 77. 34 b) 2. 0944 + 0. 0003233 + 12. 22 7. 001 = 2. 04466 = 2. 04 c) 1. 42 x 102 + 1. 021 x 103 = 3751. 613 = 3. 8 x 102 3. 1 x 10 d) (6. 1982 x 10 -4) -1 2 = 3. 841768 x 10 -7 = 3. 8418 x 10 -7 e) (2. 3232 + 0. 2034 - 0. 16) x 4. 0 x 103 = 9480 = 9500

Why the Metric System? International unit of measurement: SI units n n Base units Derived units Based on units of 10’s

LENGTH Measure distances or dimensions in space Meter (m) Length traveled by light in a vacuum in 1/299792458 seconds.

MASS Measure of quantity of matter Kilogram (kg) Mass of a prototype platinum-iridium cylinder

TIME Forward flow of events Second (s) Time is the radiation frequency of the cesium-133 atom.

VOLUME Amount of space an object occupies 3 Cubic meter (m ) Derived unit 3 1 m. L = 1 cm

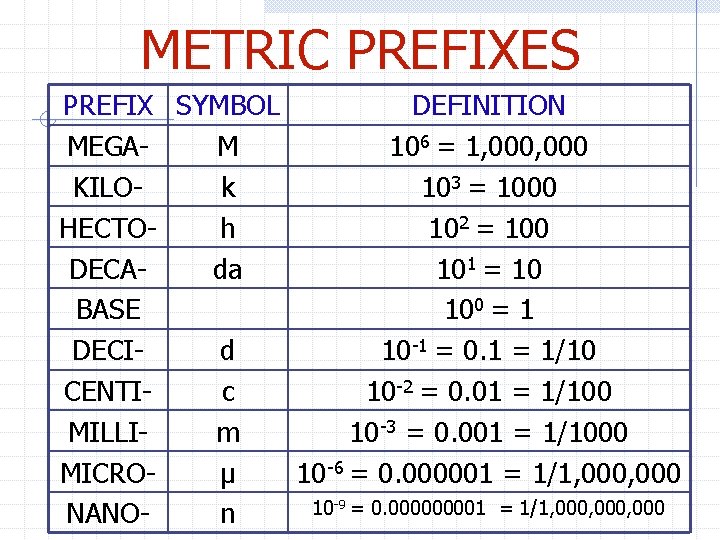
METRIC PREFIXES PREFIX SYMBOL DEFINITION MEGAM 106 = 1, 000 KILOk 103 = 1000 HECTOh 102 = 100 DECAda 101 = 10 BASE 100 = 1 DECId 10 -1 = 0. 1 = 1/10 CENTIc 10 -2 = 0. 01 = 1/100 MILLIm 10 -3 = 0. 001 = 1/1000 MICROμ 10 -6 = 0. 000001 = 1/1, 000 10 -9 = 0. 00001 = 1/1, 000, 000 NANOn

DIMENSIONAL ANALYSIS Process to solve problems Factor-Label Method Dimensions of equation may be checked

DIMENSIONAL ANALYSIS Examples: a) 3 years = _______seconds 1 year = 365 days 1 day = 24 hours 1 hour = 60 minutes 1 min = 60 seconds 3 years 365 days 24 hours 60 minutes 60 seconds 1 year 1 day 1 hour 1 minute = 94608000 seconds = 9 x 10 7 seconds

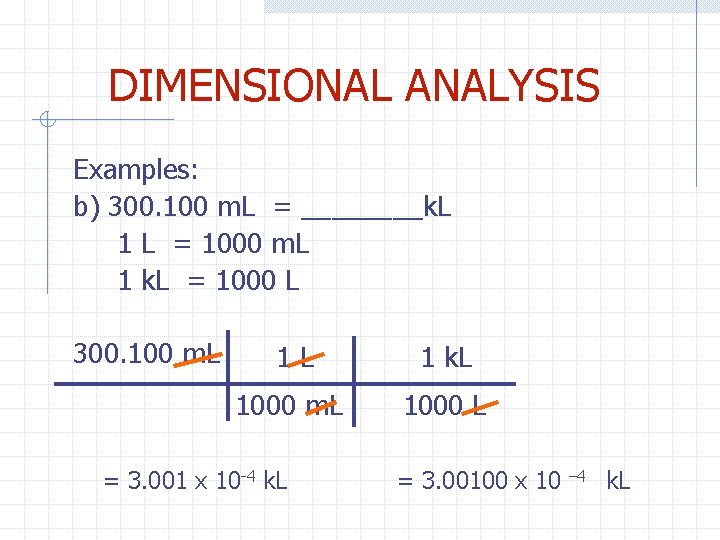
DIMENSIONAL ANALYSIS Examples: b) 300. 100 m. L = ____k. L 1 L = 1000 m. L 1 k. L = 1000 L 300. 100 m. L 1 L 1 k. L 1000 m. L 1000 L = 3. 001 x 10 -4 k. L = 3. 00100 x 10 – 4 k. L

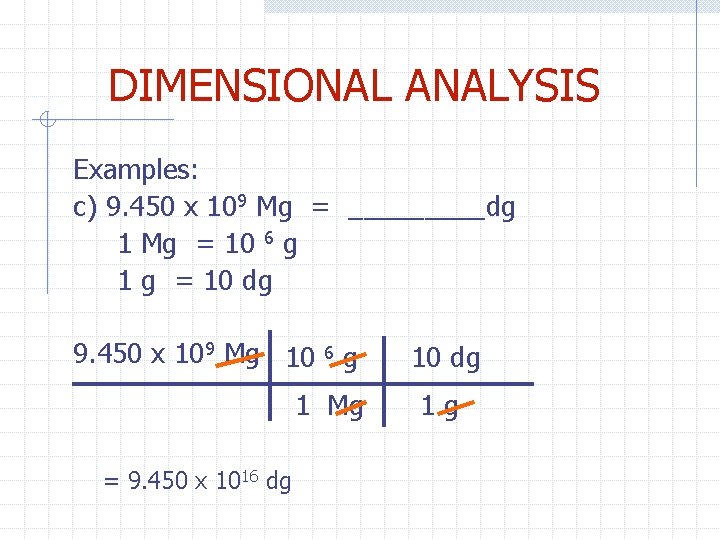
DIMENSIONAL ANALYSIS Examples: c) 9. 450 x 109 Mg = _____dg 1 Mg = 10 6 g 1 g = 10 dg 9. 450 x 109 Mg 10 6 g 1 Mg = 9. 450 x 1016 dg 10 dg 1 g

Experiment 1 : Measure and Convert Using Dimensional Analysis Lab Station 1: Measure the total width( short side) of the 2 tables Together Width =______ centimeter(cm) Show conversion using dimensional analysis Width = _______meters (m)

Lab Station 2: Measure the length (long side) of one table Length = ______ centimeter(cm) Show your conversion using dimensional analysis Length = ______meters(m)

Lab Station 3: Measure the mass of the weight using the triple beam balance : Mass = _____grams(g) Show your conversion using dimensional analysis Mass = _______kilograms(Kg)

Lab Station 4: Measure the Mass of the object using the digital scale Mass = _______ grams (g) Show your conversion using dimensional analysis Mass= _____kilogram (kg)

Lab Station 5 Measure the Volume of water using The Graduated cylinder Volume = _____ milliliter(m. L) Show your conversion using dimensional analysis Volume = _____ cubic centimeter(cc or cm 3)

Lab Station 6 : Measure the volume of a cylinder Diameter= ______ cm Height = ______cm Volume = _____cm 3 Show your conversion using dimensional analysis Volume = ______ m 3

Lab Station 7 : Measure the dimensions of the block. Length =____ cm Width =_____ cm Height = ____ cm Calculate the Volume of the Block. Show calculation Volume = ______ cm 3 Show your conversion using dimensional analysis Volume = ____ cubic meters (m 3)

Lab Station 8: Measure the distance using a meterstick. Distance = ____ centimeter(cm) Show your conversion using dimensional analysis Distance = ____ meter(m) Show your conversion using dimensional analysis Distance = ____kilometer(km)

Lab Station 9: Measure your walk time in a given distance Time = _______ seconds (sec) Show your conversion using dimensional analysis Time = _____ hour (h)

Lab Station 10 : Calculate your speed : Show your calculations Speed (v) = distance / time Speed (v) = ______ meters/sec or m/s Show your conversion using dimensional analysis Speed ( v) = ______ kilometers/ hour or km/h

Lab Station 11: Measure the Temperature of Water Temperature = _____0 F Convert the temperature to Temperature = _____0 C Temperature = _____ K

DIMENSIONAL ANALYSIS Examples: d) 2. 356 g OH- = _____ molecules OH 1 mole = 17 g OH 1 mole = 6. 022 x 10 23 molecules 2. 356 g OH - 1 mole OH 17 g OH - - 6. 022 x 1023 molecules 1 mole OH - = 8. 34578 x 1022 molecules = 8. 346 x 10 22 molecules

DIMENSIONAL ANALYSIS Examples: e) 45. 00 km = _____cm 1 km = 1000 m 1 m = 100 cm 45. 00 km 1000 m 1 km = 4500000 cm 1 m = 4. 500 x 10 6 cm

DIMENSIONAL ANALYSIS Examples: f) 6. 7 x 1099 seconds = _______years 1 year = 365 days 1 day = 24 hours 1 hour = 60 minutes 1 min = 60 seconds 6. 7 x 1099 seconds 1 minute 60 seconds 1 hours 1 day 1 year 60 minutes 24 hours 365 days = 2. 124556 x 1092 years = 2. 1 x 10 92 years

DIMENSIONAL ANALYSIS Examples: g) 1. 2400 g He = _____ Liters He 1 mole = 4 g He 1 mole = 22. 4 L 1. 2400 g He 1 mole He 4 g He 22. 4 Liters He 1 mole He = 6. 944 Liters He = 6. 9440 Liters He