4 Modeling of side chains 1 Side chain

4. Modeling of side chains 1

Side chain modeling is part of structure prediction Protein Structure Prediction: – given: – predict: sequence of protein structure of protein Challenges: – conformation space • goal: describe continuous, immense space of conformations in an efficient and representative way – realistic energy function • goal: energy minimum at or near experimentally derived structure (native) – efficient and reliable search algorithm • goal: locate minimum (global minimum energy conformation GMEC) Prediction of side chain conformations: – subtask of protein structure prediction 2

The importance of side chain modeling Side chain prediction subtask of protein structure prediction • given: correct backbone conformation • predict: side chain conformations (i. e. whole protein) • successful prediction of protein structure depends on successful prediction of the side chain conformations • complete details not solved by experiment • allows evaluation of protocol at detailed, full-atom level • allows flexibility in docking 3

Today’s menu Prediction of side chain conformations 1. rotamer libraries 2. dependence on backbone accuracy 3. approaches that locate GMEC or MECs Rosetta & other approaches DEE - Dead end elimination, SCWRL, PB - Belief propagation, LP -Linear integer programming 4

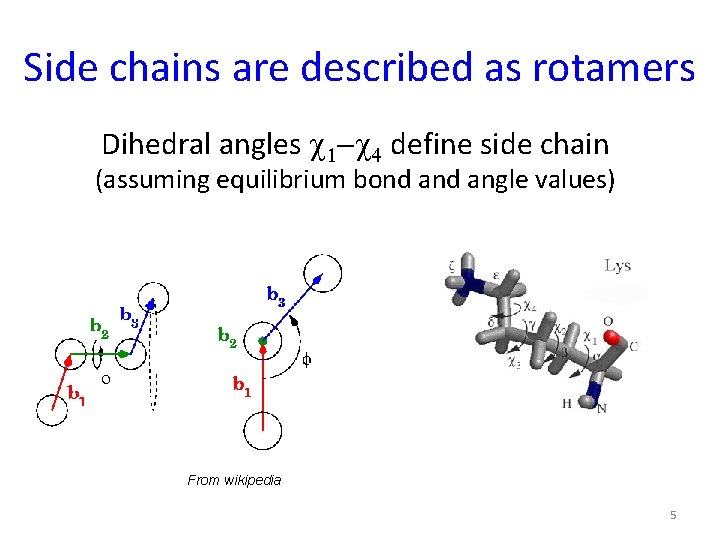
Side chains are described as rotamers Dihedral angles c 1 -c 4 define side chain (assuming equilibrium bond angle values) From wikipedia 5

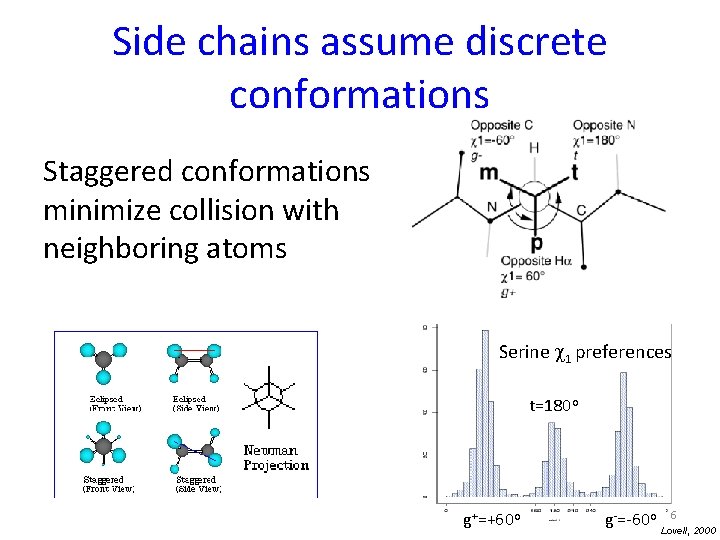
Side chains assume discrete conformations Staggered conformations minimize collision with neighboring atoms Serine c 1 preferences t=180 o g+=+60 o 6 g-=-60 o Lovell, 2000

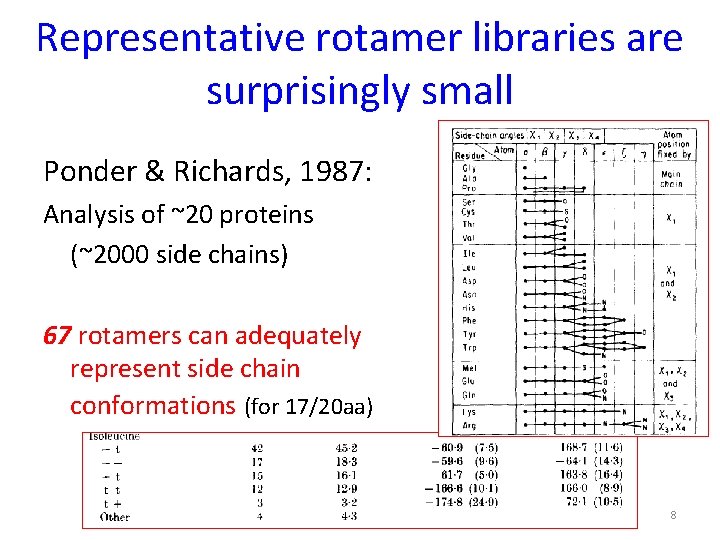
Representative rotamer libraries are surprisingly small Ponder & Richards, 1987: Analysis of ~20 proteins (~2000 side chains) 67 rotamers can adequately represent side chain conformations (for 17/20 aa) 8

Backbone dependent rotamer libraries Dunbrack & Karplus, 1993: • For each f-y (20 ox 20 o) bin, derive statistics on c 1+c 2 values • Reflects dependence of side chain conformation on backbone conformation y f 9

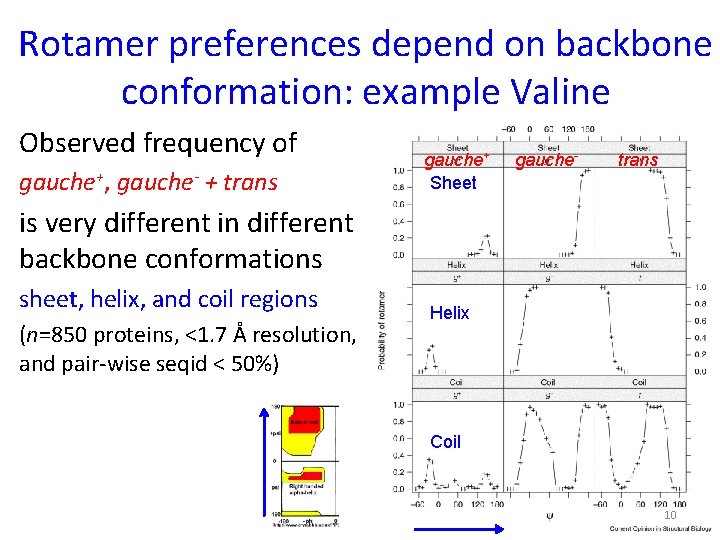
Rotamer preferences depend on backbone conformation: example Valine Observed frequency of gauche+, gauche- + trans gauche+ Sheet gauche- trans is very different in different backbone conformations sheet, helix, and coil regions (n=850 proteins, <1. 7 Å resolution, and pair-wise seqid < 50%) Helix Coil 10

Bayesian statistical analysis of rotamer library Dunbrack 1997 Estimate populations • for all rotamers, • of all side chain types, • for each f-y (10 ox 10 o) bin P(c 1| f, y) P(c 2, c 3, c 4 | c 1, f, y) using Bayesian formalism 11

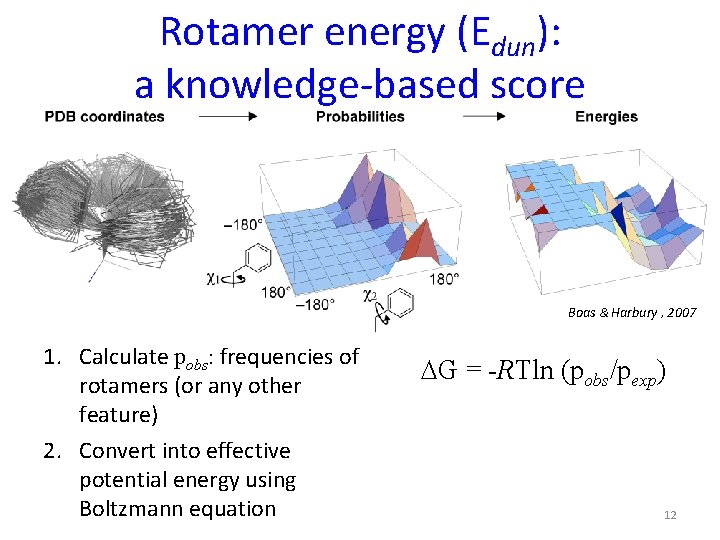
Rotamer energy (Edun): a knowledge-based score Boas & Harbury , 2007 1. Calculate pobs: frequencies of rotamers (or any other feature) 2. Convert into effective potential energy using Boltzmann equation DG = -RTln (pobs/pexp) 12

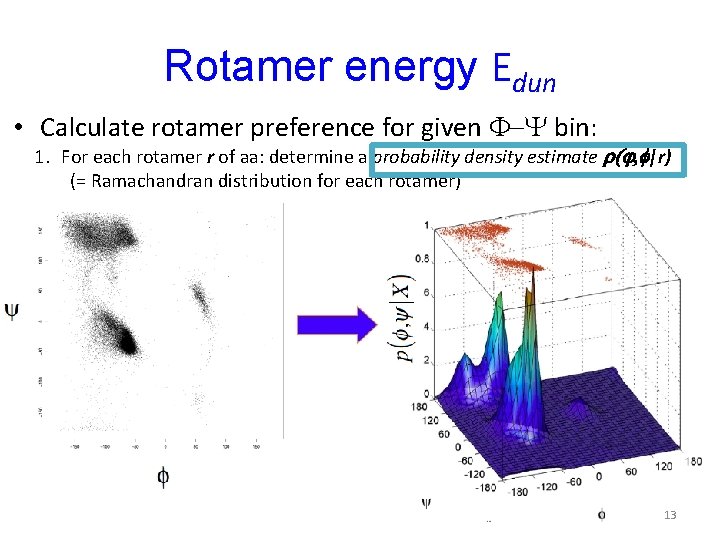
Rotamer energy Edun • Calculate rotamer preference for given F-Y bin: 1. For each rotamer r of aa: determine a probability density estimate r(j, f|r) (= Ramachandran distribution for each rotamer) 13

Rotamer energy Edun • Calculate rotamer preference for given F-Y bin: 1. For each rotamer r of aa: determine a probability density estimate r(j, f|r) (= Ramachandran distribution for each rotamer) 2. Use Bayes’ rule to invert this density to produce an estimate of the rotamer probability P(r): backbone independent probability of rotamer r 14

Bayesian statistical analysis of rotamer library Dunbrack 1997 Estimate populations • for all rotamers, • of all side chain types, • for each f-y (10 ox 10 o) bin P(c 1| f, y) P(c 2, c 3, c 4 | c 1, f, y) using Bayesian formalism Combine • prior distribution based on P(f)*Py) • fully f, y dependent data … to describe both • well-sampled regions • sparsely sampled regions 15

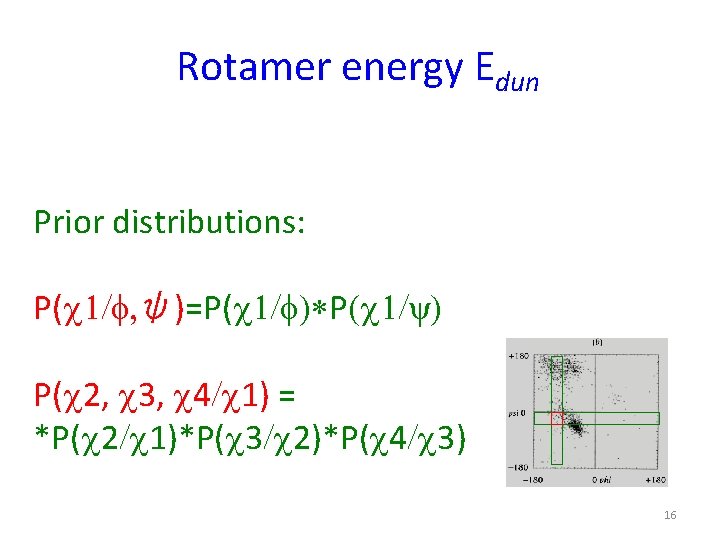
Rotamer energy Edun Prior distributions: P(c 1/f, ψ)=P(c 1/f)*P(c 1/ψ) P(c 2, c 3, c 4/c 1) = *P(c 2/c 1)*P(c 3/c 2)*P(c 4/c 3) 16

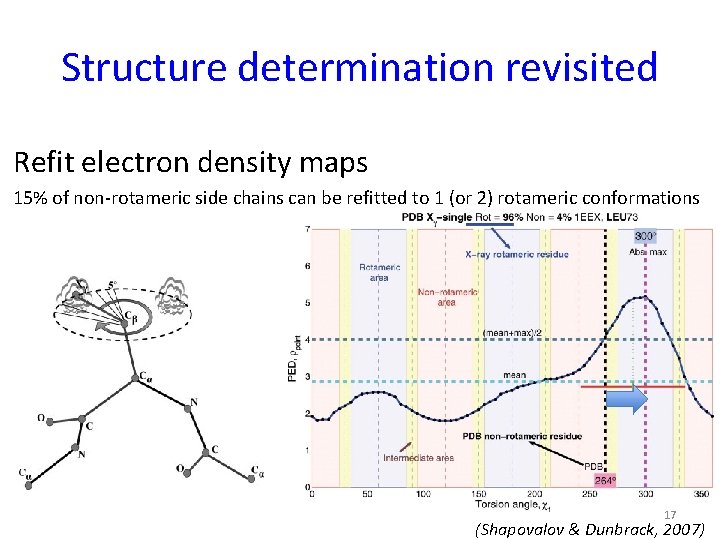
Structure determination revisited Refit electron density maps 15% of non-rotameric side chains can be refitted to 1 (or 2) rotameric conformations 17 (Shapovalov & Dunbrack, 2007)

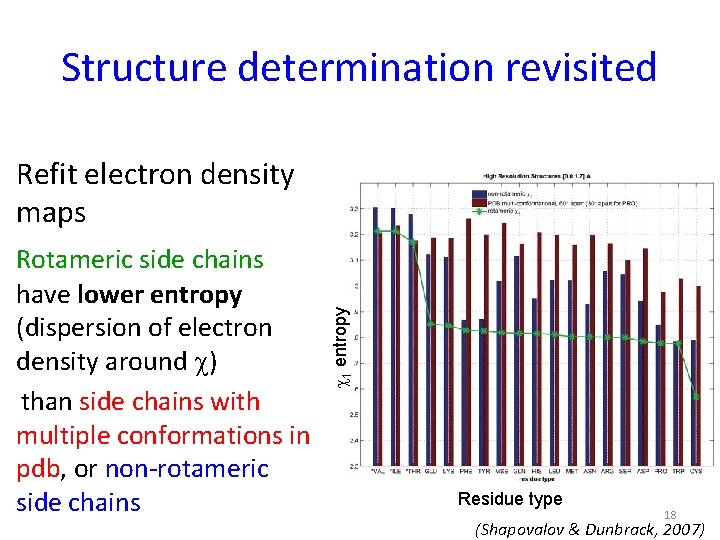
Structure determination revisited Rotameric side chains have lower entropy (dispersion of electron density around c) than side chains with multiple conformations in pdb, or non-rotameric side chains c 1 entropy Refit electron density maps Residue type 18 (Shapovalov & Dunbrack, 2007)

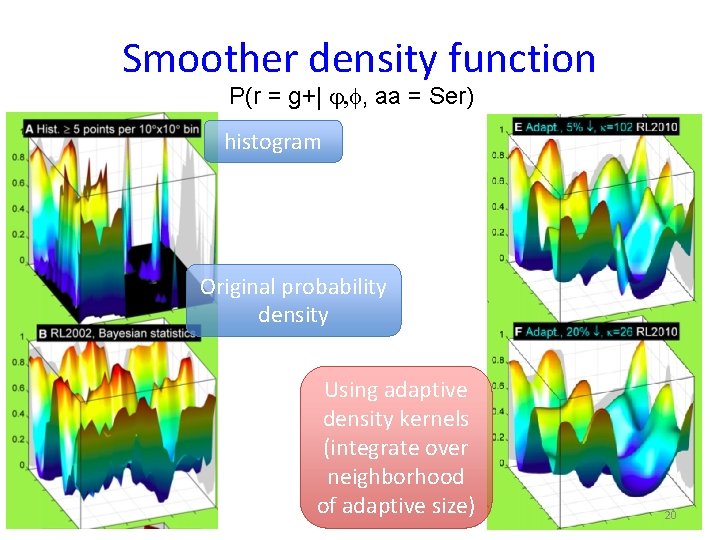
2011: Improved Dunbrack library Many good reasons: 1. More structural data 2. Improved set: Electron density calculations - remove highly dynamic side chains 3. Derive accurate and smooth density estimates of rotamer populations (incl. rare rotamers) as continuous function of backbone dihedral angles 4. Derive smooth estimates of the mean values and variances of rotameric side-chain dihedral angles 5. Improve treatment of non-rotameric degrees of freedom 19 Shapovalov & Dunbrack, 2011

Smoother density function P(r = g+| j, f, aa = Ser) histogram Original probability density Using adaptive density kernels (integrate over neighborhood of adaptive size) 20

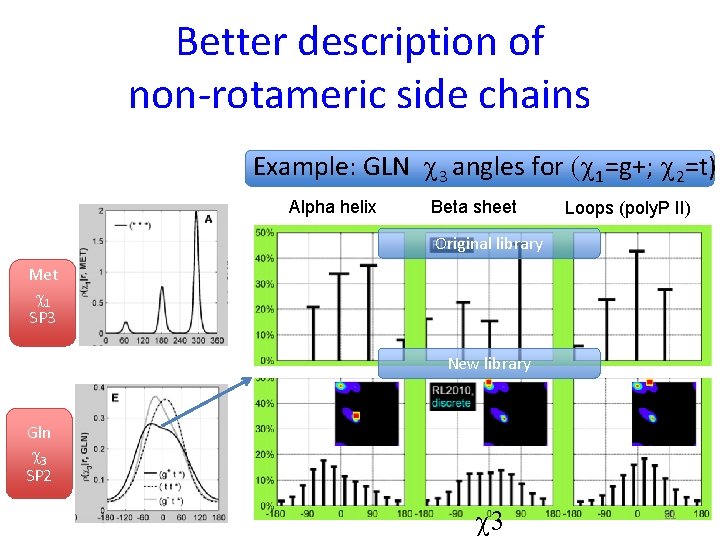
Better description of non-rotameric side chains Example: GLN c 3 angles for (c 1=g+; c 2=t) Alpha helix Beta sheet Loops (poly. P II) Original library Met c 1 SP 3 New library Gln c 3 SP 2 c 3 21

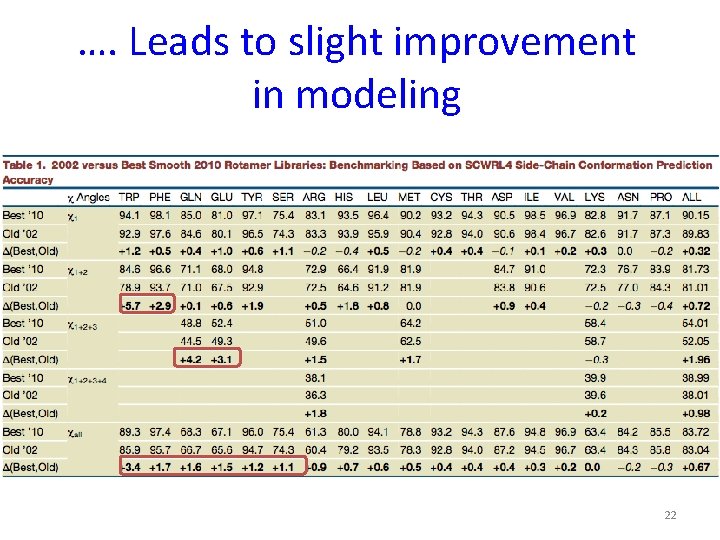
…. Leads to slight improvement in modeling 22

Some conclusions about rotamer libraries Rotamer frequency: • rare conformations reflect increased internal strain – important to take frequency into account • frequency can be used as energy term: Ei= -K ln Pi Increasing availability of high-resolution structures • narrows distribution around rotamer in library • Indicates that errors are responsible for outliers Refitting of electron density maps • non-rotameric conformations often incorrectly modeled and high in entropy 23

Some conclusions about rotamer libraries Rotamericity <100%: • Include more side chain conformations! – Position-dependent rotamers (example: unbound conformations in docking predictions) – Additional conformations around rotamer (± sd) – Non-rotameric side chain angles: describe as continuous density function 24

Today’s menu Prediction of side chain conformations 1. rotamer libraries 2. dependence on backbone accuracy 3. approaches that locate GMEC or MECs Rosetta & other approaches DEE - Dead end elimination, SCWRL, PB - Belief propagation, LP -Linear integer programming 25

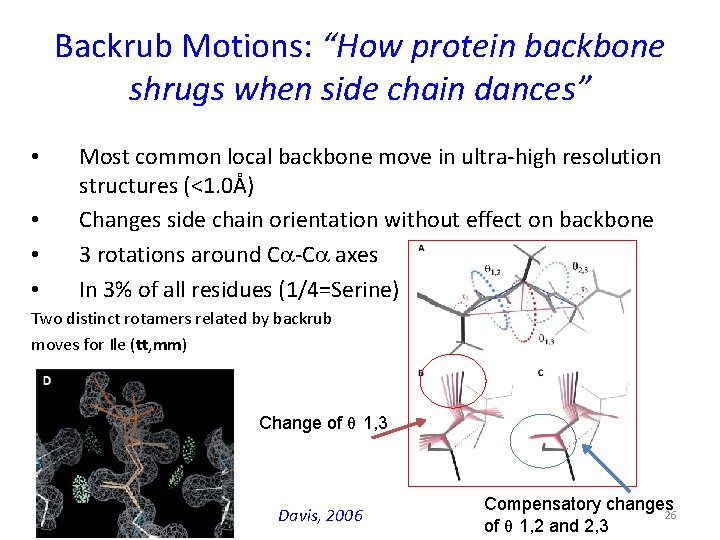
Backrub Motions: “How protein backbone shrugs when side chain dances” • • Most common local backbone move in ultra-high resolution structures (<1. 0Å) Changes side chain orientation without effect on backbone 3 rotations around Ca-Ca axes In 3% of all residues (1/4=Serine) Two distinct rotamers related by backrub moves for Ile (tt, mm) Change of θ 1, 3 Davis, 2006 Compensatory changes 26 of θ 1, 2 and 2, 3

Today’s menu Prediction of side chain conformations 1. rotamer libraries 2. dependence on backbone accuracy 3. approaches that locate GMEC or MECs Rosetta & other approaches DEE - Dead end elimination, SCWRL, PB - Belief propagation, LP -Linear integer programming 27

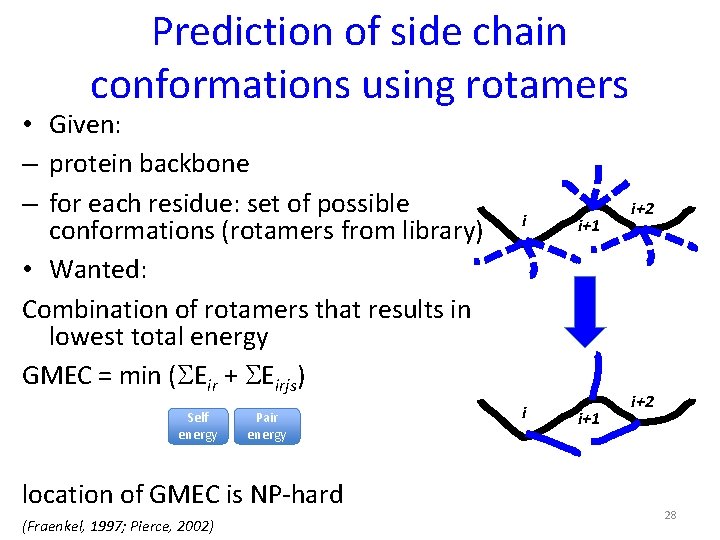
Prediction of side chain conformations using rotamers • Given: – protein backbone – for each residue: set of possible conformations (rotamers from library) • Wanted: Combination of rotamers that results in lowest total energy GMEC = min (SEir + SEirjs) Self energy Pair energy location of GMEC is NP-hard (Fraenkel, 1997; Pierce, 2002) i i i+1 i+2 28

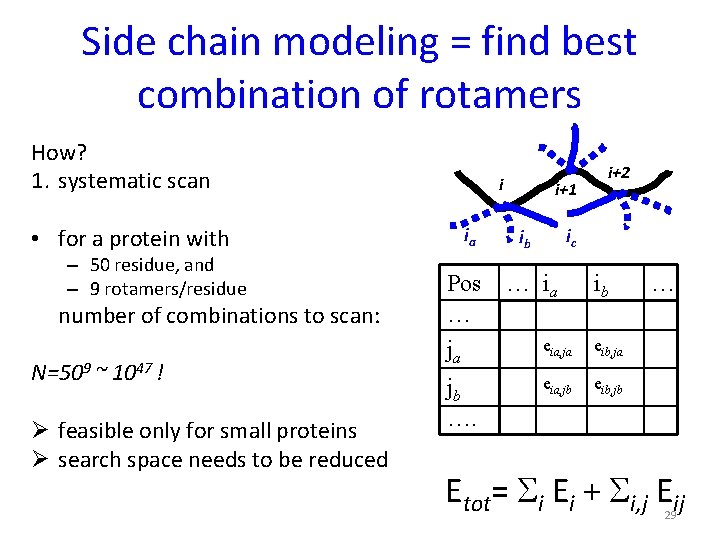
Side chain modeling = find best combination of rotamers How? 1. systematic scan • for a protein with – 50 residue, and – 9 rotamers/residue number of combinations to scan: N=509 ~ 1047 ! Ø feasible only for small proteins Ø search space needs to be reduced i ia Pos … ja jb …. i+1 i+2 ic ib … ia ib eia, ja eib, ja eia, jb eib, jb … Etot= Si Ei + Si, j Eij 29

Search strategies for locating GMEC or MECs Deterministic Approaches (e. g. DEE): – Guarantee location of GMEC – Can be slow – Advantageous when GMEC is (the only) nearnative conformation Heuristic Approaches (e. g. MC): – Locate Population of low-energy models (not necessarily GMEC) – Faster, often converge 30

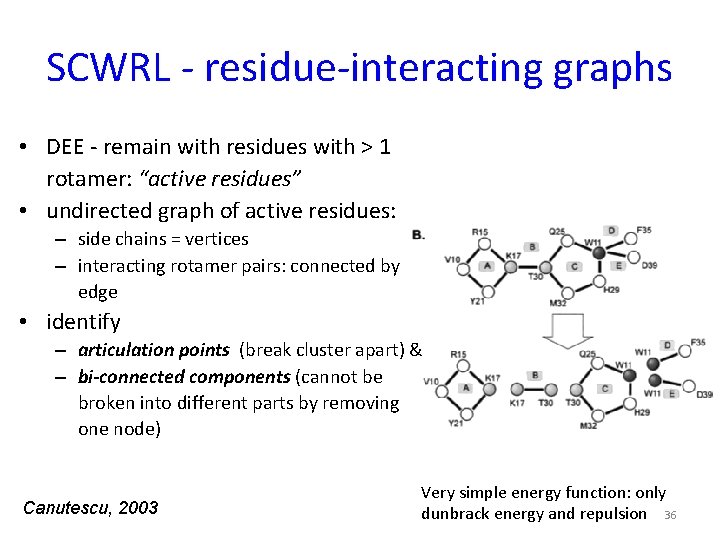
Guaranteed finding of GMEC DEE (Dead-end elimination) – prune impossible rotamers, determine GMEC from reduced rotamer set Residue-interacting graphs (SCWRL) – – use dynamic programming on graph to find GMEC start with “leafs”: residues with low connectivity in graph Linear Programming (Kingsford) – – – solve set of linear constraints can locate GMEC for sparsely connected graphs poses contrains on energy function 31

Dead End Elimination (DEE) • Approach: remove rotamers that cannot be part of the GMEC Rotamer r at position i can be eliminated if there exists a rotamer t such that: r E t Combinations of rotamers at positions j≠i • Iterative application of DEE removes many rotamers, at certain positions only one rotamer is left • (Note that some rotamers can be removed from the beginning because they clash with the backbone - too high Eit) 32 Desmet & Lasters, 1992

Refined DEE • Approach: remove rotamers that cannot be part of the GMEC, second criterion: Rotamer r at position i can be eliminated if there exists a rotamer t such that: r E t Combinations of rotamers at positions j≠i • This criterion allows removing of additional rotamers Goldstein, 1994 33

More sophisticated DEE criteria…. • Approach: remove rotamers that cannot be part of the GMEC - additional criterion: Rotamer r at position i can be eliminated if there exists rotamers t 1 and t 2 such that either t 1 or t 2 are better for E any combination: • takes more time to compute t 1 r t 2 Combinations of rotamers at positions j≠i At the end, we are left with 1 combination, or with a few combinations only, that need to be evaluated using 34 other criteria

DEE-based approaches • DEE guarantees to find GMEC… • … but may miss conformations that have only slightly worse energy • Given that the energy function is not perfect, we want to find also additional conformations with comparable energy • Approach used in Orbit: use MC to find additional low-energy combinations that resemble GMEC (we will talk about this when we discuss protein design)* 35 Dahiyat & Mayo (1997)

SCWRL - residue-interacting graphs • DEE - remain with residues with > 1 rotamer: “active residues” • undirected graph of active residues: – side chains = vertices – interacting rotamer pairs: connected by edge • identify – articulation points (break cluster apart) & – bi-connected components (cannot be broken into different parts by removing one node) Canutescu, 2003 Very simple energy function: only dunbrack energy and repulsion 36

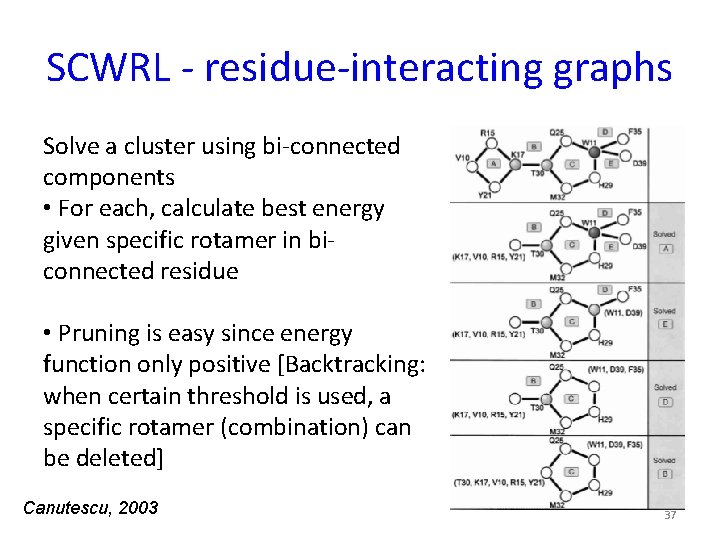
SCWRL - residue-interacting graphs Solve a cluster using bi-connected components • For each, calculate best energy given specific rotamer in biconnected residue • Pruning is easy since energy function only positive [Backtracking: when certain threshold is used, a specific rotamer (combination) can be deleted] Canutescu, 2003 37

Heuristic approaches • Define cutoff values to prune branches that probably do not contain low-energy conformations • • • Mean-field approach, Belief Propagation Self-consistent algorithms Monte-Carlo sampling 38

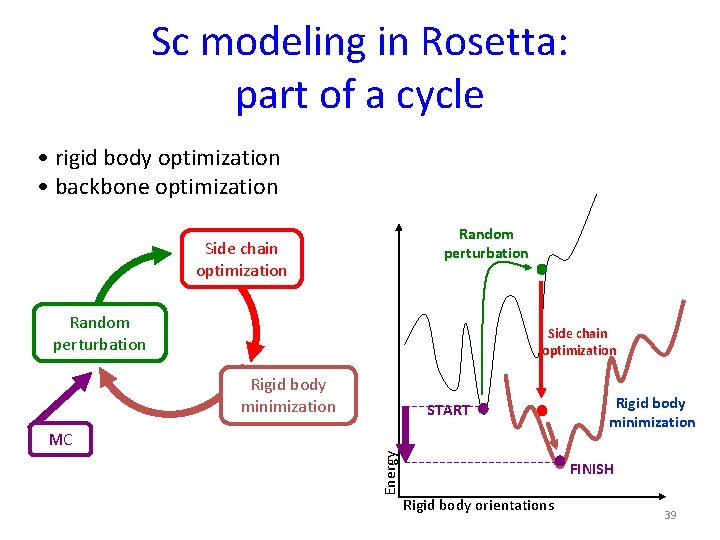
Sc modeling in Rosetta: part of a cycle • rigid body optimization • backbone optimization Random perturbation Side chain optimization Rigid body minimization START Energy MC Rigid body minimization FINISH Rigid body orientations 39

Side chain modeling protocols in Rosetta • Monte-Carlo procedure: • heuristic • does not converge – several runs needed to locate solution • Use Dunbrack bb-dependent rotamer library Approaches: 1. “Repacking” – model side chain conformation from scratch 2. “Rotamer Trial” – refine side chain conformations 3. (“Rotamer Trial with minimization” (RTmin) – off -rotamer sampling by minimization) 40

Monte Carlo sampling • Pre-calculate Eir and Eirjt matrix • Self energy: Energy between rotamer r at position i with constant part • Pairwise energy: between rotamer r at position i and rotamer t at position j (sparse matrix) Etotal = Si Eir + Si. Sj Eirjt • Simulated annealing • make random change • start with high acceptance rate, gradually lower temperature • acceptance based on Boltzmann distribution 41

“Repacking”: full combinatorial side chain optimization • remove all side chains • gradually add side chains: select from backbonedependent rotamer library add position-specific rotamers (e. g. from unbound conformation): set their energy to minimum rotamer energy, to ensure acceptance • use simulated annealing to create increasingly well packed side chains • repeat to sample range of low-energy conformations 42

“Rotamer trial”: side chain adjustment • Find better rotamers for existing structure • pick residue at random • search for rotamer with lower energy • replace rotamer • Repeated until all high-energy positions are improved • Fast 43

Side chain modeling: Summary • Side chain modeling based on rotamer libraries Combinatorial problem • Approaches for side chain modeling involve smart reduction of combinatorial complexity (heuristic or exact) • Side chain modeling as a “toy model” for structural modeling • Side chain modeling can be extended to Design by adding rotamer options of different amino acids 45