4 Hankel Functions H 1 x H 2









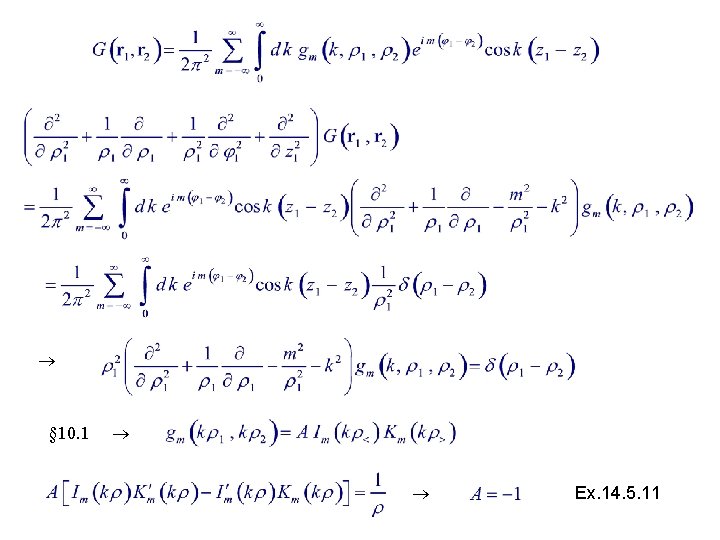


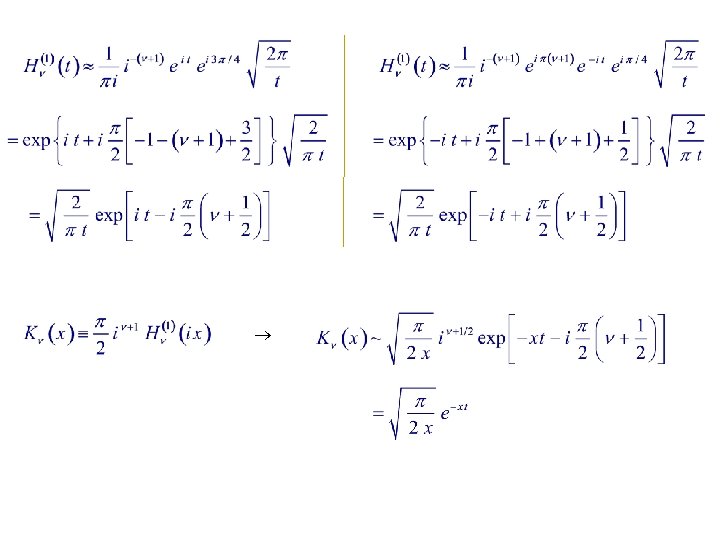

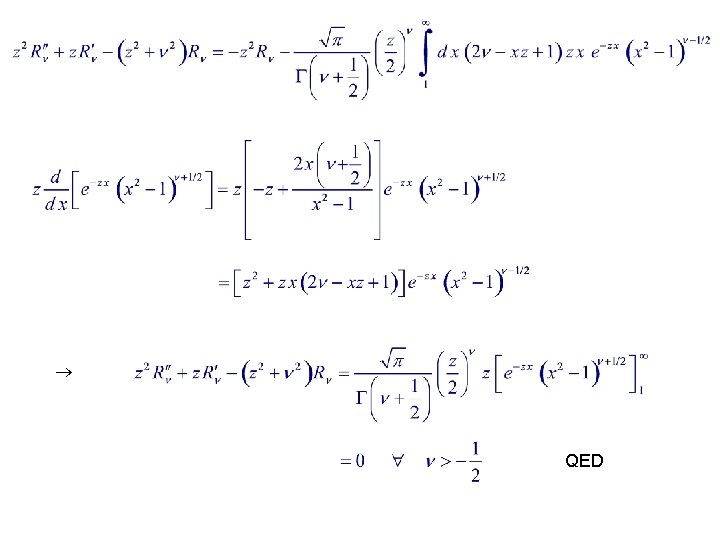





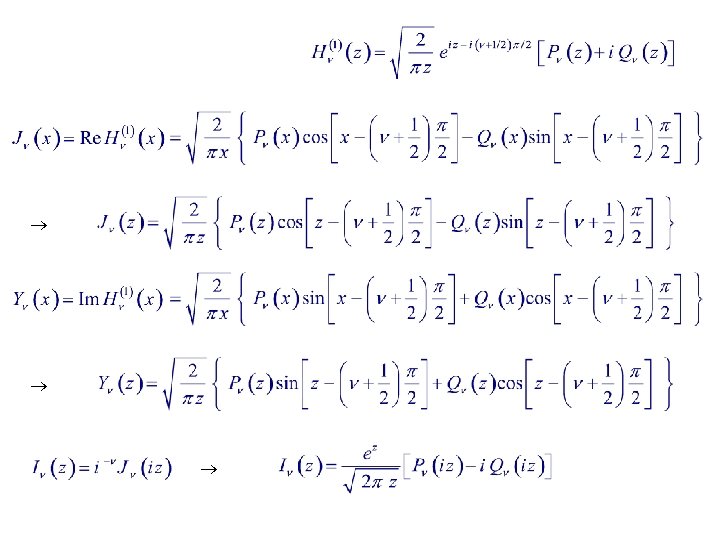








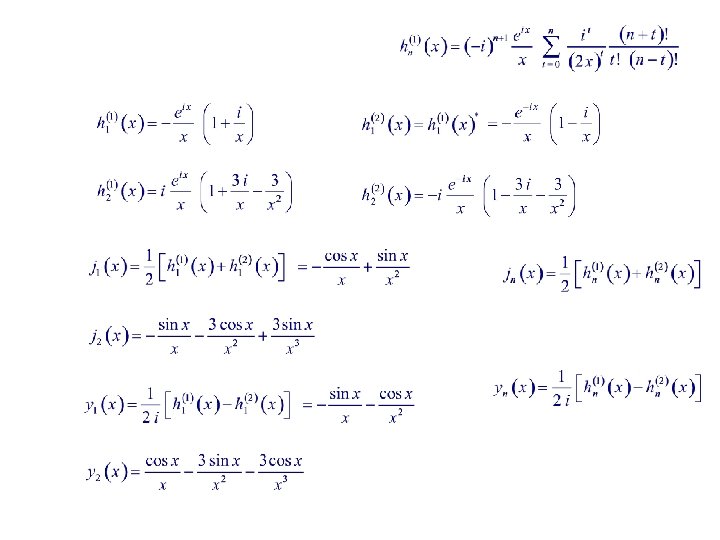











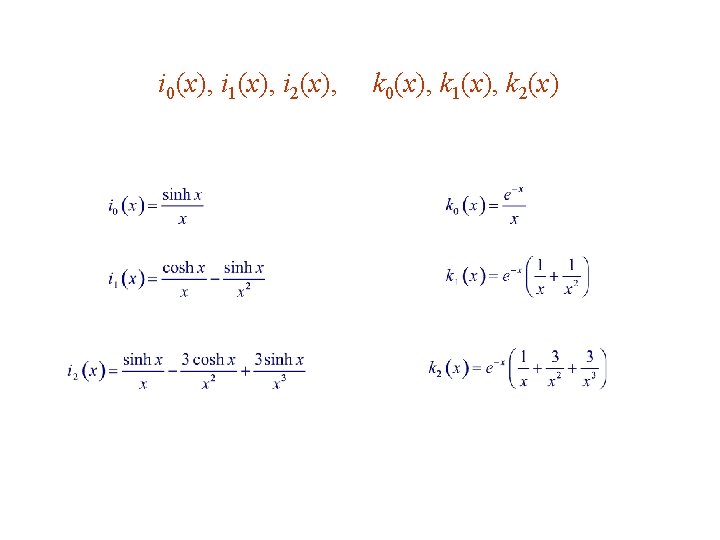


- Slides: 52

4. Hankel Functions, H (1) (x) & H (2) (x) Hankel functions of the 1 st & 2 nd kind : c. f. for x real For x << 1, >0:

Recurrence Relations

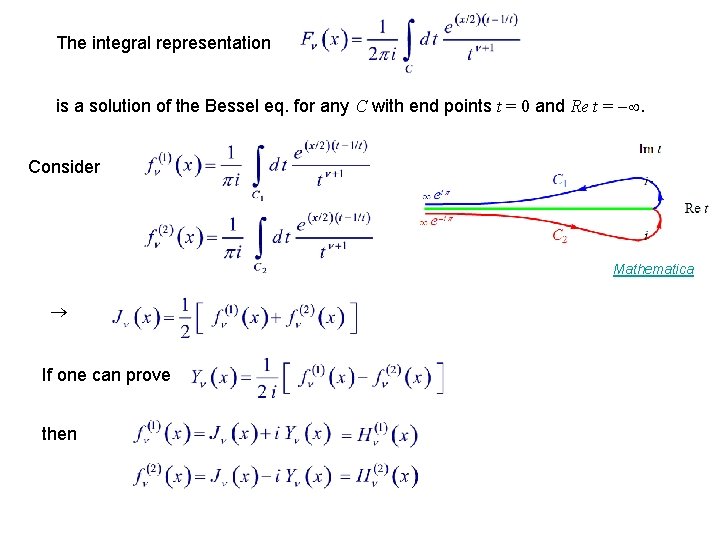
Contour Representations See Schlaefli integral The integral representation is a solution of the Bessel eq. if at end points of C.

The integral representation is a solution of the Bessel eq. for any C with end points t = 0 and Re t = . Consider Mathematica If one can prove then

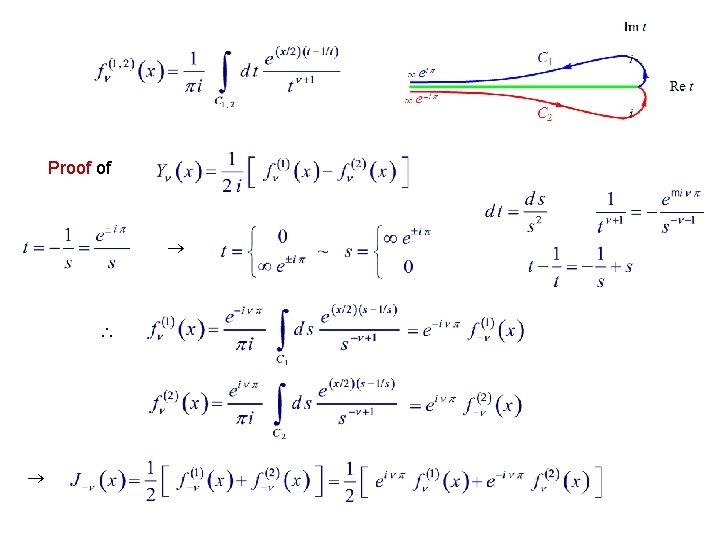
Proof of

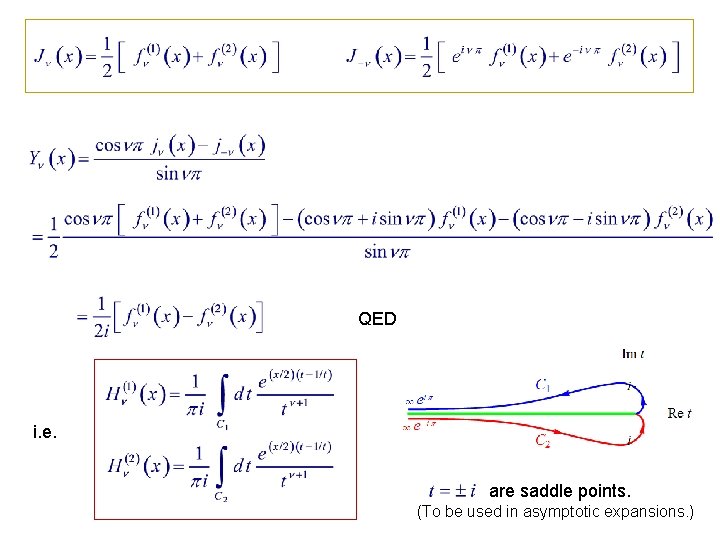
QED i. e. are saddle points. (To be used in asymptotic expansions. )

5. Modified Bessel Functions, I (x) & K (x) Bessel equation : oscillatory Modified Bessel equation : Modified Bessel functions Bessel eq. exponential Modified Bessel eq. are all solutions of the MBE.

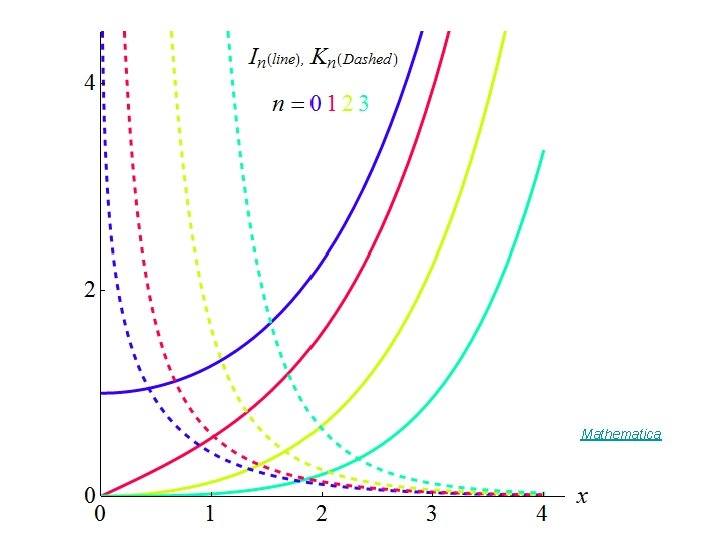
I (x) Modified Bessel functions of the 1 st kind : I (x) is regular at x = 0 with

Mathematica

Recurrence Relations for I (x)

2 nd Solution K (x) Modified Bessel functions of the 2 nd kind ( Whitaker functions ) : Recurrence relations : For x 0 : Ex. 14. 5. 9

Integral Representations Ex. 14. 5. 14

Example 14. 5. 1. A Green’s Function Green function for the Laplace eq. in cylindrical coordinates : Let
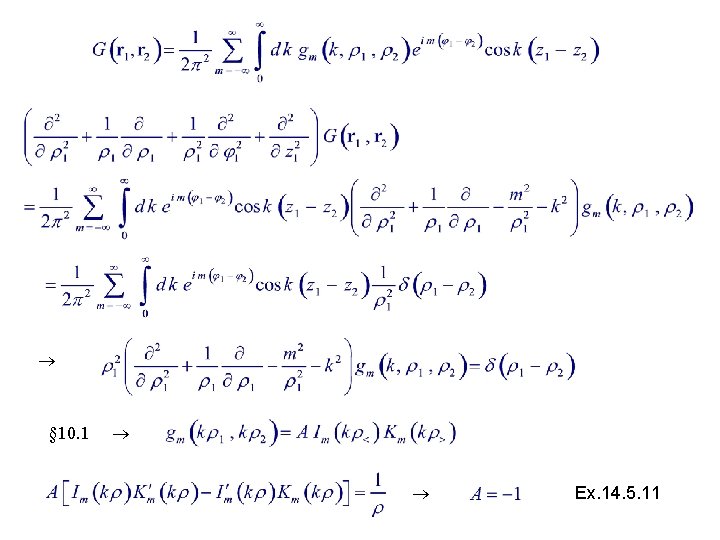
§ 10. 1 Ex. 14. 5. 11

5. Asymptotic Expansions 1. Expansion in negative powers [ Stokes’ method (Ex 14. 6. 10. ) ]. Problem : Relation to named functions not known. 2. Steepest descent.

Asymptotic Forms of H Contour integral representation: Method of steepest descent ( § 12. 7 ) :
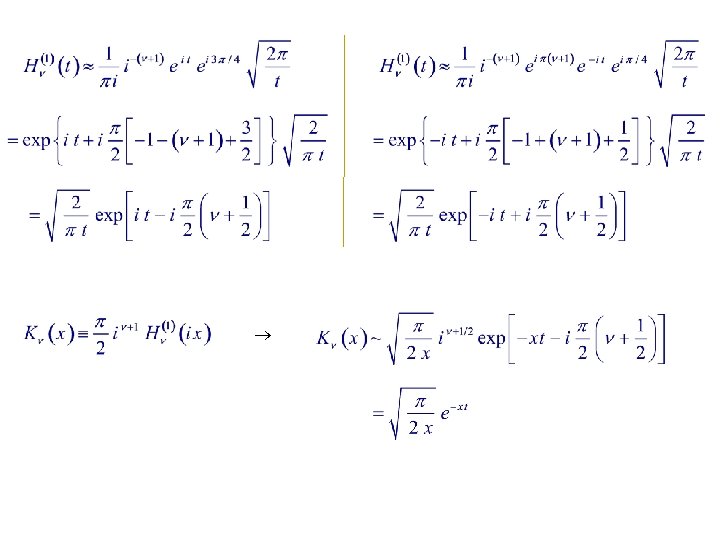

Expansion of an Integral Representation for K Consider Proof : 1. R satisfies the MBE.
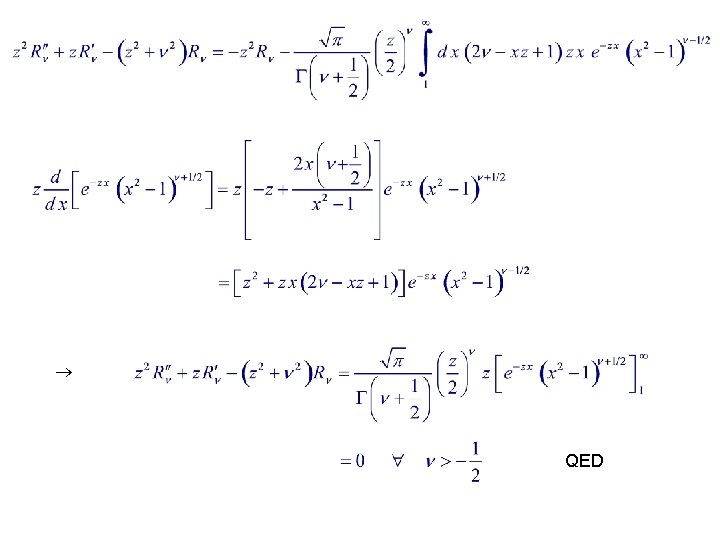
QED

Proof : Let 2. R = K for z 0. QED

Proofs 1 & 2 R = K i. e. Proof : 3. K (z) decays exponentially for large z. QED

is a divergent asymptotic series Series terminates for z = is an essential singularity No convergent series solution about z = .


Additional Asymptotic Forms Asymptotic forms of other Bessel functions can be expressed in terms of P & Q . Analytic continued to all z :
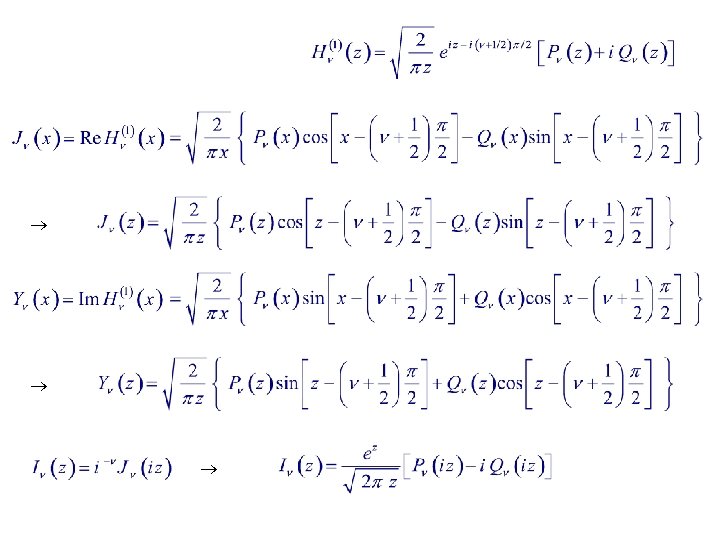

Properties of the Asymptotic Forms All Bessel functions have the asymptotic form where e. g. good for

Mathematica

Example 14. 6. 1. Eg. 14. 1. 24 : Cylindrical Traveling Waves 2 -D vibrating circular membrane standing waves Consider 2 -D vibrating circular membrane without boundary travelinging waves For large r Circular symmetry (no dependence ) : diverges at r = 0

6. Spherical Bessel Functions Radial part of the Helmholtz eq. in spherical coordinates Spherical Bessel functions

Definitions Spherical Bessel functions ( integer orders only ) :

where Pochhammer symbol


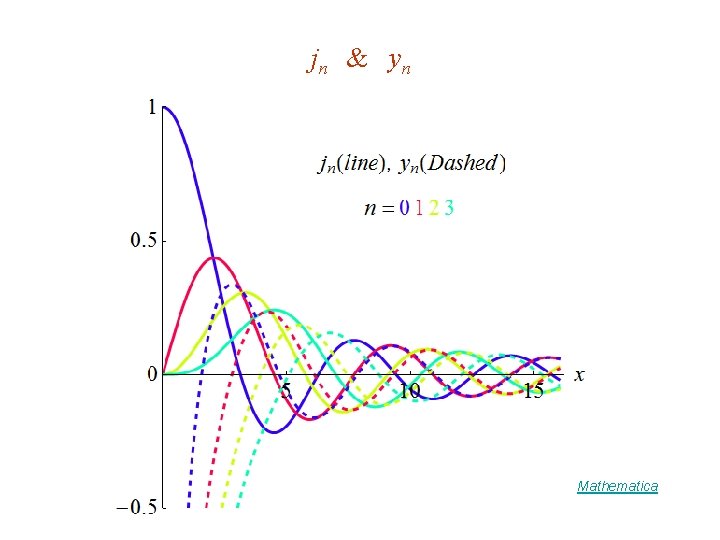
jn & yn Mathematica


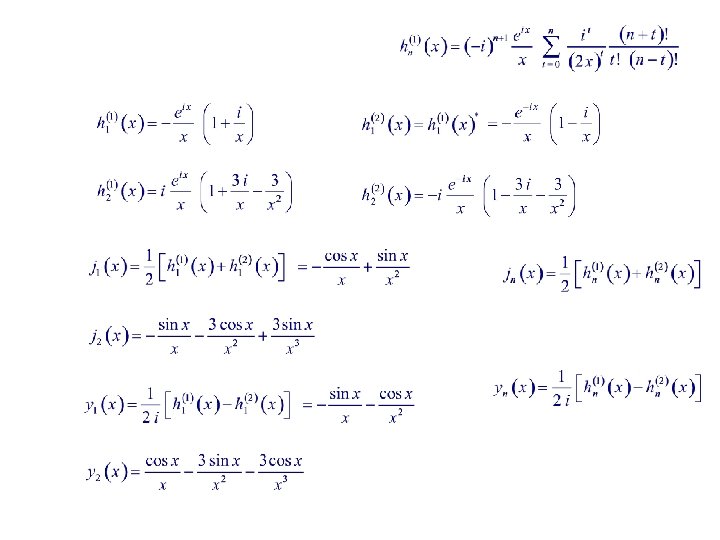

For any Bessel functions Recurrence Relations F (x) = J (x) , Y (x) , H (1, 2)(x) : For any spherical Bessel functions fn (x) = jn (x) , yn(x) , hn(1, 2)(x) :


Rayleigh Formulas Proof is by induction.

Proof of Rayleigh Formula For n = 1 : Assuming case n to be true, QED

Limiting Values : x << 1 For x << 1 :

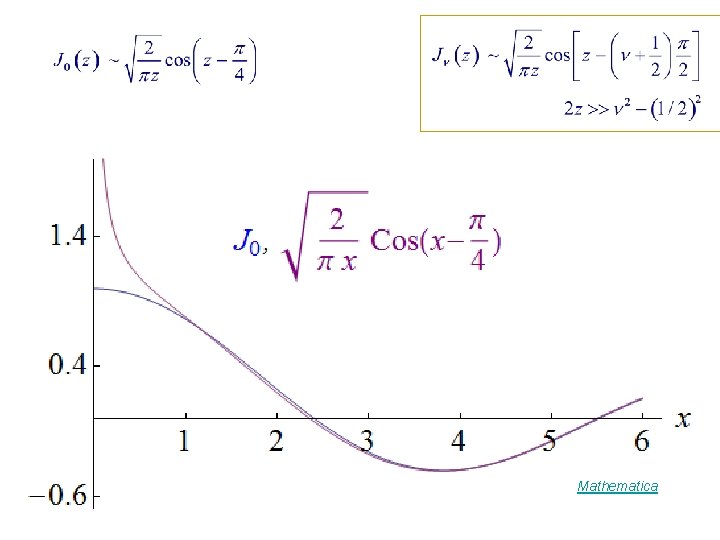
Limiting Values : x >> n ( n + 1 ) / 2 Standing spherical waves Travelling spherical waves

Orthogonality & Zeros Set r. Note: n i for jn is numerically the same as n+1/2, i for Jn+1/2, .

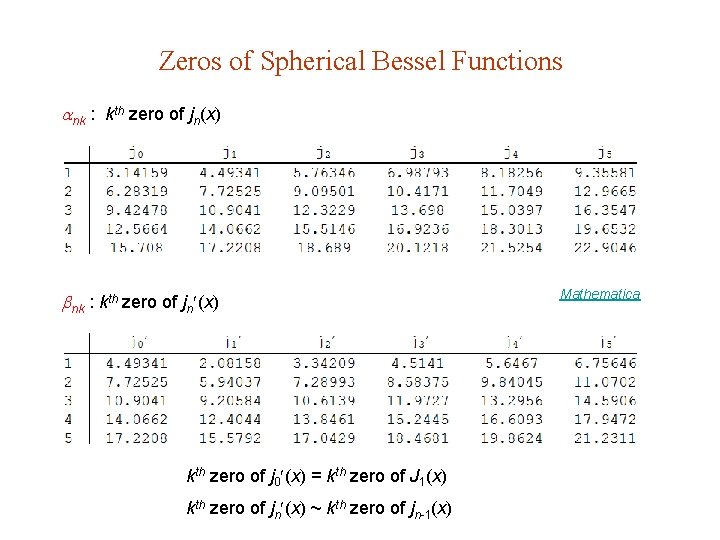
Zeros of Spherical Bessel Functions nk : kth zero of jn(x) nk : kth zero of jn (x) kth zero of j 0 (x) = kth zero of J 1(x) kth zero of jn (x) ~ kth zero of jn-1(x) Mathematica

Example 14. 7. 1. Particle in a Sphere Schrodinger eq. for free particle of mass m in a sphere of radius a : with Radial eq. for r a : R is regular at r = 0 B=0 quantized

General remarks : 1. Spatial confinement 2. Finite zero-point energy ( uncertainty principle ). 3. E is angular momentum dependent. 4. Eigenfunction belonging to same l but different n are orthogonal. energy quantization. More Orthogonality : Ex. 14. 7. 12 -3

Modified Spherical Bessel Functions Spherical Bessel equation : Modified Spherical Bessel equation : Caution :

Recurrence Relations
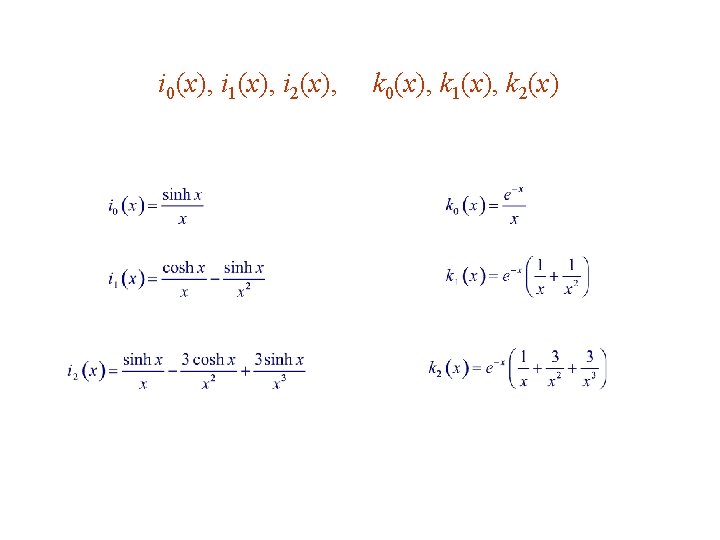
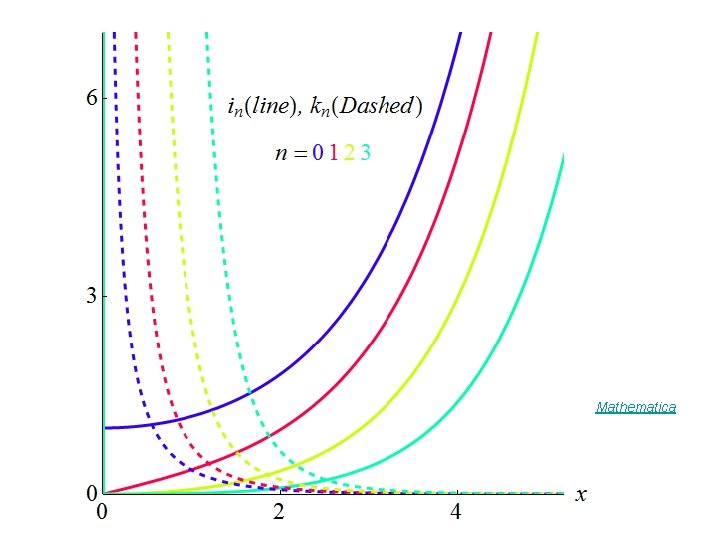
i 0(x), i 1(x), i 2(x), k 0(x), k 1(x), k 2(x)

Mathematica

Limiting Values For x << 1 : For x >> 1 :

Example 14. 7. 2. Particle in a Finite Spherical Well Schrodinger eq. for free particle of mass m in a well of radius a : with Radial eq. : Bound states : V 0 < E < 0 Smooth connection : Numerical solution