4 Duality dual and primal problems Conts Final

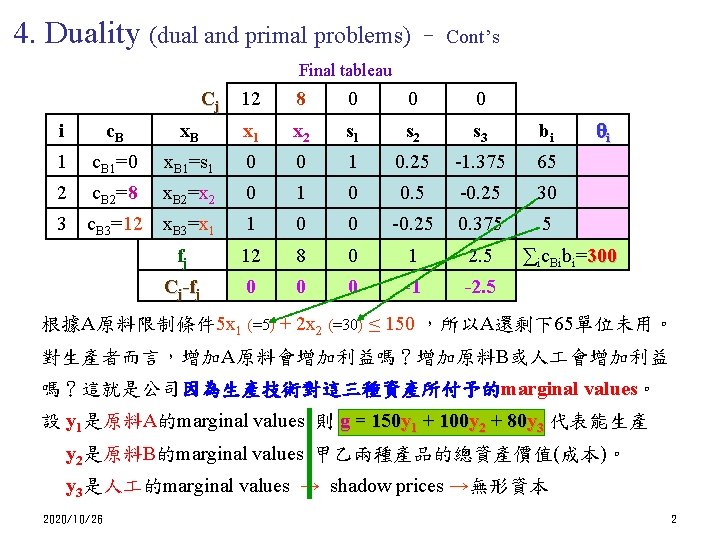
4. Duality (dual and primal problems) – Cont’s Final tableau Cj 12 8 0 0 0 i c. B x 1 x 2 s 1 s 2 s 3 bi 1 c. B 1=0 x. B 1=s 1 0 0 1 0. 25 -1. 375 65 2 c. B 2=8 x. B 2=x 2 0 1 0 0. 5 -0. 25 30 3 c. B 3=12 x. B 3=x 1 1 0 0 -0. 25 0. 375 5 fj 12 8 0 1 2. 5 Cj-fj 0 0 0 -1 -2. 5 i ∑ic. Bibi=300 根據A原料限制條件 5 x 1 (=5) + 2 x 2 (=30) ≤ 150 ，所以A還剩下65單位未用。 對生產者而言，增加A原料會增加利益嗎？增加原料B或人 會增加利益 嗎？這就是公司因為生產技術對這三種資產所付予的marginal values。 設 y 1是原料A的marginal values 則 g = 150 y 1 + 100 y 2 + 80 y 3 代表能生產 y 2是原料B的marginal values 甲乙兩種產品的總資產價值(成本)。 y 3是人 的marginal values → shadow prices →無形資本 2020/10/26 2

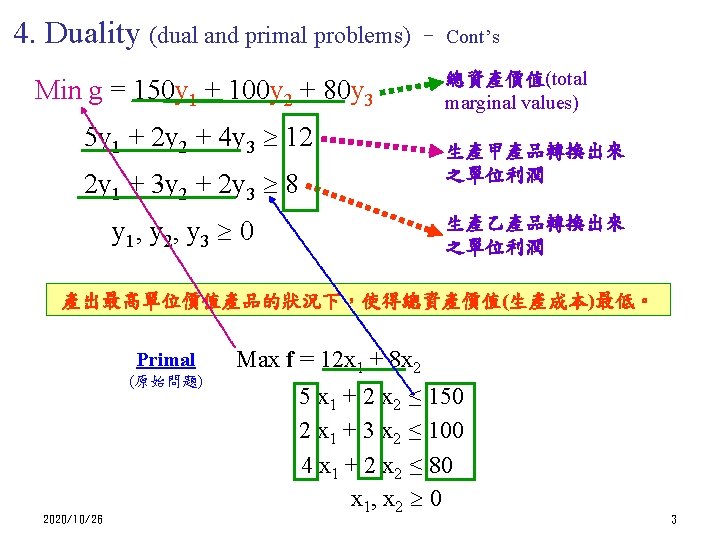
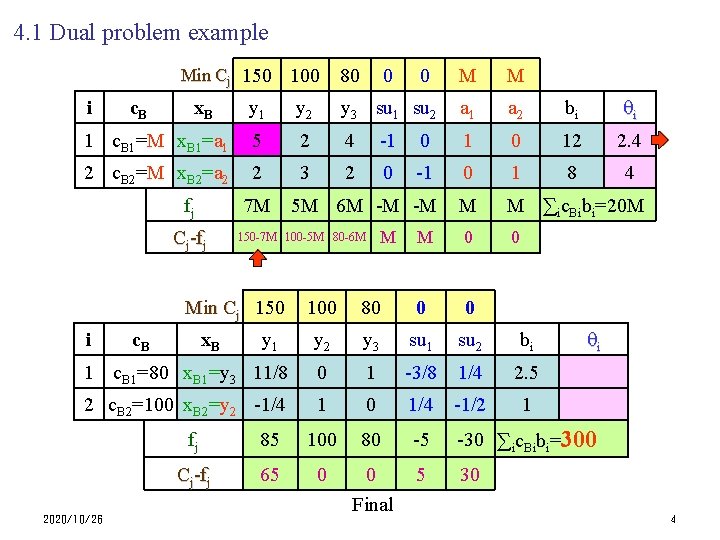
4. 1 Dual problem example Min Cj 150 100 80 0 0 M M y 1 y 2 y 3 su 1 su 2 a 1 a 2 bi i 1 c. B 1=M x. B 1=a 1 5 2 4 -1 0 12 2. 4 2 c. B 2=M x. B 2=a 2 2 3 2 0 -1 0 1 8 4 7 M 5 M 6 M -M -M M M ∑ic. Bibi=20 M M 0 0 i c. B x. B fj Cj-fj M 150 -7 M 100 -5 M 80 -6 M Min Cj 150 100 80 0 0 y 2 y 3 su 1 su 2 bi 1 c. B 1=80 x. B 1=y 3 11/8 0 1 -3/8 1/4 2. 5 2 c. B 2=100 x. B 2=y 2 -1/4 1 0 1/4 -1/2 1 i 2020/10/26 c. B x. B y 1 i fj 85 100 80 -5 -30 ∑ic. Bibi=300 Cj-fj 65 0 0 5 30 Final 4

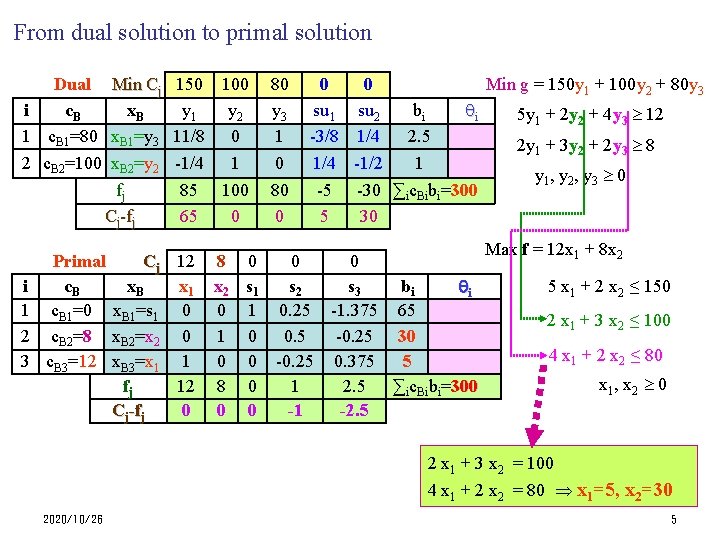
From dual solution to primal solution Min g = 150 y 1 + 100 y 2 + 80 y 3 Dual Min Cj 150 100 i c. B x. B y 1 y 2 1 c. B 1=80 x. B 1=y 3 11/8 0 80 y 3 1 0 su 1 -3/8 0 su 2 1/4 bi 2. 5 2 c. B 2=100 x. B 2=y 2 -1/4 1 0 1/4 -1/2 1 100 0 80 0 -5 5 -30 ∑ic. Bibi=300 30 fj Cj-fj 85 65 Primal Cj 12 i c. B x 1 1 c. B 1=0 x. B 1=s 1 0 2 c. B 2=8 x. B 2=x 2 0 3 c. B 3=12 x. B 3=x 1 1 fj 12 Cj-fj 0 i 5 y 1 + 2 y 2 + 4 y 3 12 8 0 0 0 x 2 s 1 s 2 s 3 bi i 0 1 0. 25 -1. 375 65 1 0 0. 5 -0. 25 30 0 0 -0. 25 0. 375 5 8 0 1 2. 5 ∑ic. Bibi=300 0 0 -1 -2. 5 2 y 1 + 3 y 2 + 2 y 3 8 y 1, y 2, y 3 0 Max f = 12 x 1 + 8 x 2 5 x 1 + 2 x 2 ≤ 150 2 x 1 + 3 x 2 ≤ 100 4 x 1 + 2 x 2 ≤ 80 x 1, x 2 0 2 x 1 + 3 x 2 = 100 4 x 1 + 2 x 2 = 80 x 1=5, x 2=30 2020/10/26 5

4. 2 Primal vs Dual Example x 1 Max f = [12, 8] x 2 T Primal Max f = c x 5 2 150 x 1 2 3 100 x 2 4 2 80 Ax b i = 1, …, m; xj 0 Dual x 0 a 31 x 2 0 Transpose Min g = b. Ty ATy c a 13 y 1 Min g = [150, 100, 80] y 2 y 3 y 1 5 2 4 12 y 2 2 3 2 8 y 3 j = 1, …, n; yi 0 2020/10/26 y 0 y 1 y 2 0 y 3 6

4. 2. 1 Canonical Forms for dual problem construction ☻先把問題轉換成Canonical form。 Ø求極大值的問題：constraints全部轉成 ≤ 的不等式。 Ø求極小值的問題：constraints全部轉成 的不等式。 Max f = 10 x 1 + 6 x 2 2 x 1 + 3 x 2 ≤ 90 4 x 1 + 2 x 2 ≤ 80 x 2 15 -x 2 ≤ -15 5 x 1 + x 2 = 25 5 x 1 + x 2 ≤ 25 x 1, x 2 0 5 x 1 + x 2 25 -5 x 1 - x 2 ≤ -25 2020/10/26 4 x 1 + 2 x 2 ≤ 80 -x 2 ≤ -15 5 x 1 + x 2 ≤ 25 -5 x 1 - x 2 ≤ -25 x 1, x 2 0 7

4. 2. 1 Canonical Forms for dual problem construction (cont’) Max f Max = 10 x 1 + 6 x 2 2 x 1 + 3 x 2 ≤ 90 4 x 1 + 2 x 2 ≤ 80 - 1 x 2 ≤ -15 5 x 1 + 1 x 2 ≤ 25 -5 x 1 - 1 x 2 ≤ -25 x 1, x 2 0 Min g Min = 90 y 1 + 80 y 2 - 15 y 3 + 25 y 4 - 25 y 5 2 y 1 + 4 y 2 + 5 y 4 - 5 y 5 10 3 y 1 + 2 y 2 - 1 y 3 + 1 y 4 - 1 y 5 6 y 1, y 2, y 3, y 4, y 5 0 2020/10/26 8

4. 3 Duality Theorems (from Max to Min) 2020/10/26 9

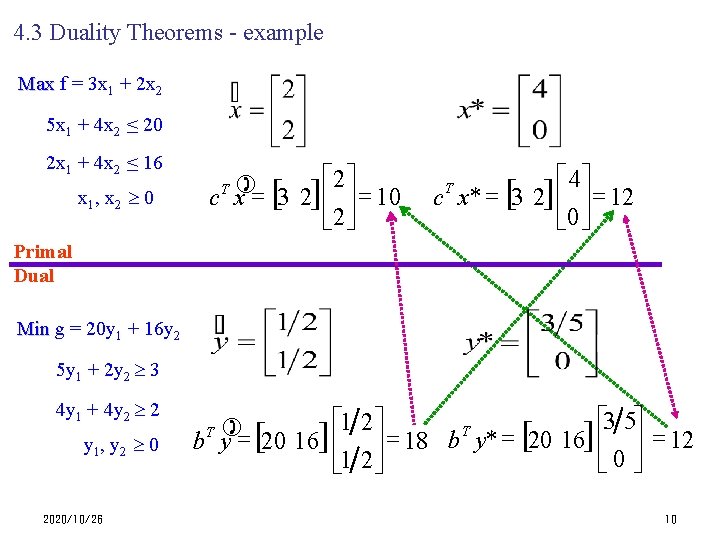
4. 3 Duality Theorems - example Max f Max = 3 x 1 + 2 x 2 5 x 1 + 4 x 2 ≤ 20 2 x 1 + 4 x 2 ≤ 16 x 1, x 2 0 é 2ù ) c x = [3 2] ê ú = 10 ë 2û T é 4ù c x* = [3 2] ê ú = 12 ë 0û T Primal Dual Min g Min = 20 y 1 + 16 y 2 5 y 1 + 2 y 2 3 4 y 1 + 4 y 2 2 y 1, y 2 0 2020/10/26 é 3 5ù é 1 2ù T ) b y = [20 16] ê ú = 18 b y* = [20 16] ê ú = 12 ë 0 û ë 1 2û T 10

4. 3 Duality Theorems - cont’ • 2020/10/26 11