4 Disorder and transport in DMS anomalous Hall

4. Disorder and transport in DMS, anomalous Hall effect, noise § Disorder and transport in DMS • Weak potential disorder scattering: Semiclassical transport theory • Strong potential disorder scattering • Interlude: Spatial defect correlations • Lightly doped DMS: Percolation picture • Anomalous Hall effect

Disorder and transport in DMS Why should disorder be important? insulating/localized Direct observations: § some samples are Anderson insulators § metallic samples have high residual resistivity (k. Fl is not large) low § metal-insulator transition Physical reasoning: metallic § many dopands (acceptors/donors) in random positions § compensation → low carrier density → weak electronic screening § compensation → charged defects CB 2+ 1– 1– VB high

What type of disorder? Example: (Ga, Mn)As Single Mn acceptor: Binding energy is ~3/4 due to Coulomb attraction, ~1/4 to exchange → Coulomb potential disorder gives larger contribution Coulomb disorder is strongly enhanced by presence of compensating defects § antisites As. Ga (double donors) § interstitials Mni (double donors) Fully aligned impurity spins & “large” wave functions (not strongly localized) → each carrier sees many aligned spins → mean-field limit, weak exchange disorder Mac. Donald et al. , Nature Materials 4, 195 (2005) Moral: Neglecting Coulomb but keeping J is questionable

Weak potential disorder scattering: Semiclassical transport theory Boltzmann equation: without scattering the phase-space density does not change in the comoving frame k Thus r vk: velocity, F: force Disorder scattering described by scattering integral: with

“in” “out” transition rate from |k´ i to |k i due to disorder derivation from full equation of motion of density operator : see Kohn & Luttinger, PR 108, 590 (1957) How can we calculate W? Assume the disorder potential to be a small perturbation V: → Leading order perturbation theory (see, e. g. , Landau/Lifschitz, vol. 3) For a periodic perturbation V = F e–i t the transition rate is k space element

§ static perturbation: let ! 0 and F ! V § potential consists of random short-range scatterers: this gives shift r (l l´ terms drop out under averaging over impurity configurations) integration over 3 k: leads to (ni = Nimp/Volume: density of impurities)

§ elastic: energy does not change § explicitly symmetric in k and k´ (not so in higher orders!) For scatterers, and thus , we get Here W is a constant, apart from the energy-conservation factor For later convenience we write this constant as (defining 1/ ) N(0): density of states at Fermi energy

Semiclassical equations of motion: Consider a wave packet narrow in r and k space Equations of motion for average position and momentum (short notation): integration by parts

since Similarly:

In homogeneous electromagnetic field: (c = 1) Thus Writing and dropping h…i we obtain for parabolic band (~ = 1) Resistivity: In steady state , then the current density is then (parabolic band) Drude conductivity D

Normal Hall effect: Assume , E component perpendicular to j follows from Hall electric field Thus the Hall conductivity is and the Hall coefficient

DMS: Additional spin scattering with impurity spins distribution of local magnetic quantum numbers, m = –S, …, S paramagnetic phase (T > Tc): Drude resistivity with total scattering rate ferromagnetic phase (T < Tc): complicated; different density of states for ", # etc. spin-orbit effects can be included: C. T. et al. , PRB 69, 115202 (2004)

Strong potential disorder scattering Strong disorder goes beyond the previous description. Approaches: § diagrammatic disorder perturbation theory (not discussed here) § numerical diagonalization Example: VB holes in (Ga, Mn)As see potential of charged defects • substitutional Mn : Q = – 1 • antisites As : Q = +2 • Mn-interstitials: Q = +2 Ga Ga l l l rscr: electronic screening length

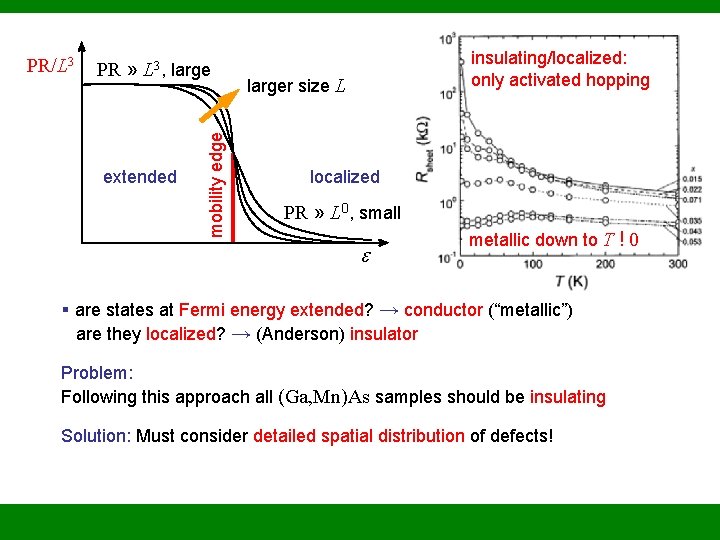
Method: C. T. , Schäfer & von Oppen, PRL 89, 137201 (2002) § write H in suitable basis (here: Hband is parabolic, choose plane waves) § numerical diagonalization → spectrum, eigenfunctions § calculate participation ratios for all eigenstates with normalization extended states (conducting): localized states (insulating): PR distinguishes between extended and localized states

PR » L 3, large extended mobility edge PR/L 3 insulating/localized: only activated hopping larger size L localized PR » L 0, small metallic down to T ! 0 § are states at Fermi energy extended? → conductor (“metallic”) are they localized? → (Anderson) insulator Problem: Following this approach all (Ga, Mn)As samples should be insulating Solution: Must consider detailed spatial distribution of defects!

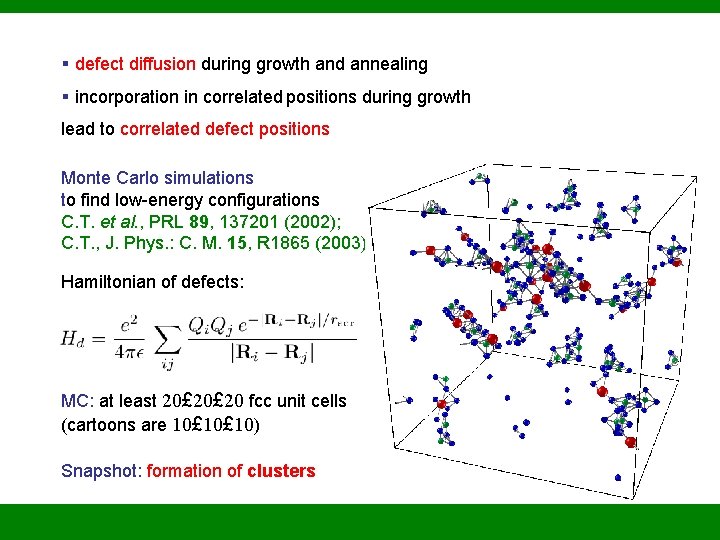
Interlude: Spatial defect correlations Why not fully random defects? many defects of charges – 1 and +2, compensation (few holes), weak screening of Coulomb interaction large Coulomb energy of defects random defects cost high energy

§ defect diffusion during growth and annealing § incorporation in correlated positions during growth lead to correlated defect positions Monte Carlo simulations to find low-energy configurations C. T. et al. , PRL 89, 137201 (2002); C. T. , J. Phys. : C. M. 15, R 1865 (2003) Hamiltonian of defects: MC: at least 20£ 20 fcc unit cells (cartoons are 10£ 10) Snapshot: formation of clusters

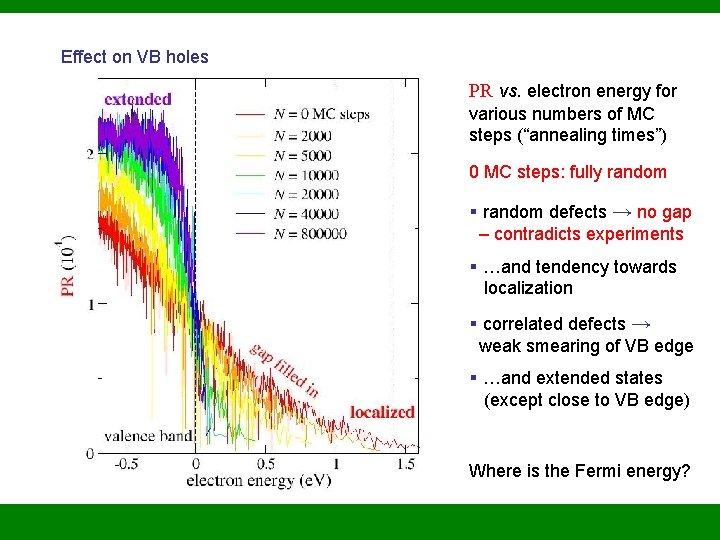
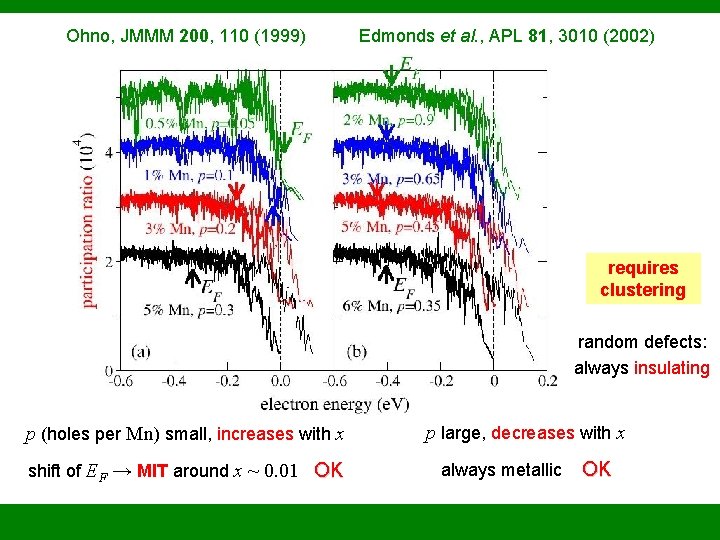
Effect on VB holes PR vs. electron energy for various numbers of MC steps (“annealing times”) 0 MC steps: fully random § random defects → no gap – contradicts experiments § …and tendency towards localization § correlated defects → weak smearing of VB edge § …and extended states (except close to VB edge) Where is the Fermi energy?

Ohno, JMMM 200, 110 (1999) Edmonds et al. , APL 81, 3010 (2002) requires clustering random defects: always insulating p (holes per Mn) small, increases with x shift of EF → MIT around x ~ 0. 01 OK p large, decreases with x always metallic OK

Lightly doped DMS: Percolation picture For low concentrations x of magnetic impurities in III-V DMS Kaminski & Das Sarma, PRB 68, 235210 (2003) following Berciu & Bhatt (2001), Erwin & Petukhov (2002), Fiete et al. (2003) etc. § hole in hydrogenic impurity state, spin antiparallel to impurity moment: Bound magnetic polaron (BMP) § low concentration: transport by thermally activated hopping from BMP to empty impurity site → conductivity vanishes for T ! 0 § higher concentration → percolation → conducting § ferromagnetism if aligned clusters percolate, transport/magnetic percolation governed by different energies (Lecture 5) § no structure in resistivity at Tc since only sparse percolating cluster orders

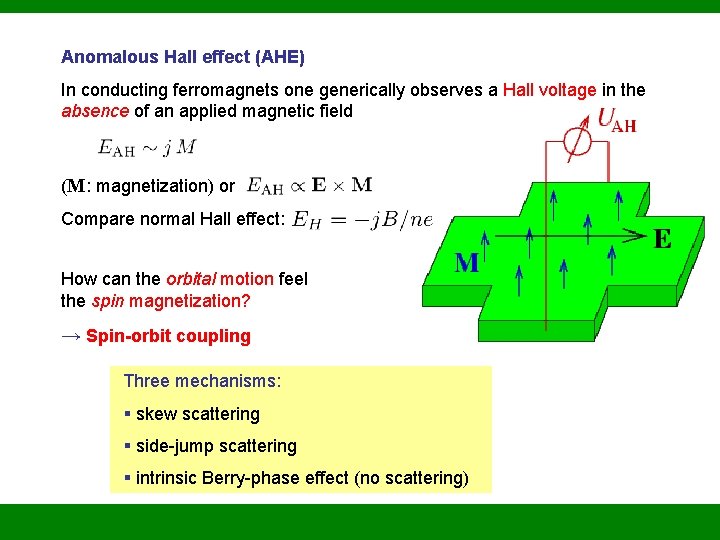
Anomalous Hall effect (AHE) In conducting ferromagnets one generically observes a Hall voltage in the absence of an applied magnetic field (M: magnetization) or Compare normal Hall effect: How can the orbital motion feel the spin magnetization? → Spin-orbit coupling Three mechanisms: § skew scattering § side-jump scattering § intrinsic Berry-phase effect (no scattering)

(1) Skew scattering Smit (1958), Kondo (1962) etc. § pure potential scattering § band structure with spin-orbit coupling: kin t ! – 1 k out 1 ! t scattering region • in bulk crystals, e. g. , k ¢ p • in assymmetric quantum well: Rashba term Scattering theory (second-order Born approximation) gives contribution to Hall resistivity Note: opposite situation, spin-orbit scattering of carriers in bands without spin-orbit coupling is sometimes also called skew scattering

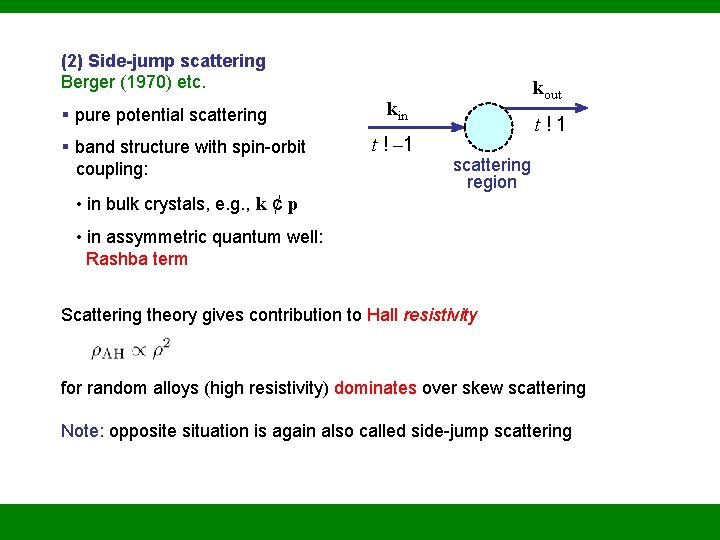
(2) Side-jump scattering Berger (1970) etc. § pure potential scattering § band structure with spin-orbit coupling: • in bulk crystals, e. g. , k ¢ p kout kin t ! – 1 t!1 scattering region • in assymmetric quantum well: Rashba term Scattering theory gives contribution to Hall resistivity for random alloys (high resistivity) dominates over skew scattering Note: opposite situation is again also called side-jump scattering

(3) Intrinsic k space Berry-phase Karplus & Luttinger, PR 95, 1154 (1954) Jungwirth, Niu & Mac. Donald, PRL 88, 207208 (2002) § no scattering necessary (intrinsic effect) § band structure with spin-orbit coupling Example: p-type DMS, 4 -band spherical approximation H(k) commutes with (projection of j onto k) → simultaneous eigenstates eigenvalues of : j = – 3/2, – 1/2, 3/2 heavy holes light holes heavy holes

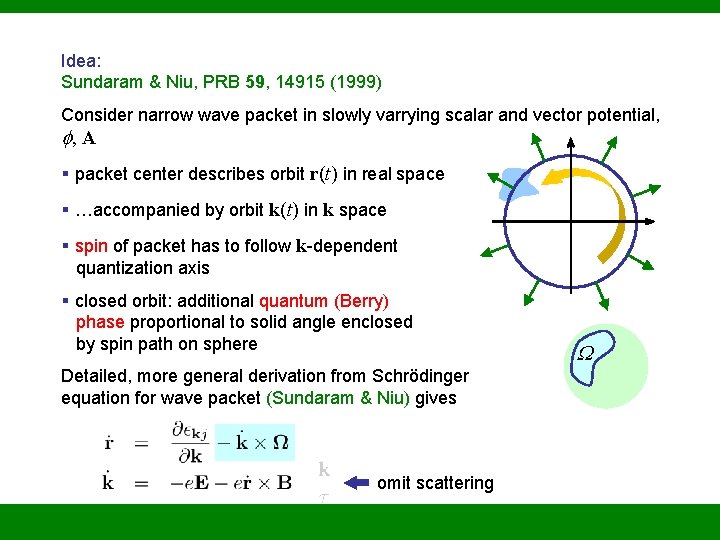
Idea: Sundaram & Niu, PRB 59, 14915 (1999) Consider narrow wave packet in slowly varrying scalar and vector potential, , A § packet center describes orbit r(t) in real space § …accompanied by orbit k(t) in k space § spin of packet has to follow k-dependent quantization axis § closed orbit: additional quantum (Berry) phase proportional to solid angle enclosed by spin path on sphere Detailed, more general derivation from Schrödinger equation for wave packet (Sundaram & Niu) gives omit scattering

with the Berry curvature where |ui is the periodic part of the Bloch function – essentially the spin part In the absence of an appied magnetic field acts like an inhomogeneous magnetic field in k space For heavy holes: Now obtain the current density

Fermi function For E along x direction and M along z () along M by symmetry): Jungwirth et al. , PRL 88, 207208 (2002) § independent of scattering term in Boltzmann equation (intrinsic) § contribution to Hall conductivity, not resistivity § AH is indeed proportional to magnetization (if not too large), in agreement with experiments § correct order of magnitude (6 -band model)

Anomalous Hall effect above Tc C. T. , von Oppen & Höfling, PRB 69, 115202 (2004) In the paramagnetic phase Does the AHE play any role here? Idea: the temporal correlation function does not vanish § gives nonzero Hall voltage noise § related to dynamical susceptibility: Start from Boltzmann equations potential scattering holes: impurity spins: spin-flip scattering j, m: magnetic quantum numbers of holes / impurities

Define hole and impurity magnetizations (z components) in 4 -band subspace scattering integrals also contain overlap integrals of spin states Derive hydrodynamic equations for the magnetizations, e. g. , for holes: Bh, Bi are effective fields containing coupling to i, h, respectively Note anisotropic diffusion term

Anisotropic spin diffusion § from spin-orbit coupling in VB § fastest along axis of local magnetization From hydrodynamic equations obtain magnetic susceptibilities of holes / impurities (non-equilibrium magnetization in z direction) t = (T–Tc)/Tc Dynamics of collective spinwave modes is purely diffusive and anisotropic

From impurity susceptibility obtain anomalous Hall voltage noise § assume intrinsic Berry-phase origin → contribution to Hall conductivity § relate correlations of Hall voltage to correlations of impurity spins § integrate over time to obtain noise U: applied voltage, Li: Hall-bar dimensions, : detector band width Noise is critically enhanced for T ! Tc