4 Adhoc I Hierarchical clustering Hierarchical versus Flat

4. Ad-hoc I: Hierarchical clustering Hierarchical versus Flat methods generate a single partition into k clusters. The number k of clusters has to be determined by the user ahead of time. Hierarchical methods generate a hierarchy of partitions, i. e. • a partition P 1 into 1 clusters (the entire collection) • a partition P 2 into 2 clusters … • a partition Pn into n clusters (each object forms its own cluster) It is then up to the user to decide which of the partitions reflects actual sub-populations in the data.

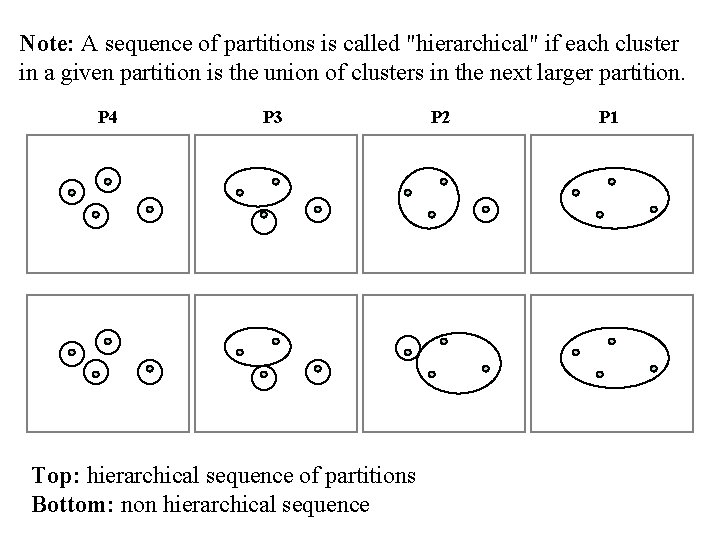
Note: A sequence of partitions is called "hierarchical" if each cluster in a given partition is the union of clusters in the next larger partition. P 4 P 3 Top: hierarchical sequence of partitions Bottom: non hierarchical sequence P 2 P 1

Hierarchical methods again come in two varieties, agglomerative and divisive. Agglomerative methods: • Start with partition Pn, where each object forms its own cluster. • Merge the two closest clusters, obtaining Pn-1. • Repeat merge until only one cluster is left. Divisive methods • Start with P 1. • Split the collection into two clusters that are as homogenous (and as different from each other) as possible. • Apply splitting procedure recursively to the clusters.

Note: Agglomerative methods require a rule to decide which clusters to merge. Typically one defines a distance between clusters and then merges the two clusters that are closest. Divisive methods require a rule for splitting a cluster.

4. 1 Hierarchical agglomerative clustering Need to define a distance d(P, Q) between groups, given a distance measure d(x, y) between observations. Commonly used distance measures: 1. d 1(P, Q) = min d(x, y), for x in P, y in Q ( single linkage ) 2. d 2(P, Q) = ave d(x, y), for x in P, y in Q ( average linkage ) 3. d 3(P, Q) = max d(x, y), for x in P, y in Q ( complete linkage ) 4. ( centroid method ) 5. ( Ward’s method ) d 5 is called Ward’s distance.

Motivation for Ward’s distance: • Let Pk = P 1 , …, Pk be a partition of the observations into k groups. • Measure goodness of a partition by the sum of squared distances of observations from their cluster means: • Consider all possible (k-1)-partitions obtainable from Pk by a merge • Merging two clusters with smallest Ward’s distance optimizes goodness of new partition.

4. 2 Hierarchical divisive clustering There are divisive versions of single linkage, average linkage, and Ward’s method. Divisive version of single linkage: • Compute minimal spanning tree (graph connecting all the objects with smallest total edge length. • Break longest edge to obtain 2 subtrees, and a corresponding partition of the objects. • Apply process recursively to the subtrees. Agglomerative and divisive versions of single linkage give identical results (more later).

Divisive version of Ward’s method. Given cluster R. Need to find split of R into 2 groups P, Q to minimize or, equivalently, to maximize Ward’s distance between P and Q. Note: No computationally feasible method to find optimal P, Q for large |R|. Have to use approximation.

Iterative algorithm to search for the optimal Ward’s split Project observations in R on largest principal component. Split at median to obtain initial clusters P, Q. Repeat { Assign each observation to cluster with closest mean Re-compute cluster means } Until convergence Note: • Each step reduces RSS(P, Q) • No guarantee to find optimal partition.

Divisive version of average linkage Algorithm Diana, Struyf, Hubert, and Rousseuw, pp. 22

4. 3 Dendograms Result of hierarchical clustering can be represented as binary tree: • Root of tree represents entire collection • Terminal nodes represent observations • Each interior node represents a cluster • Each subtree represents a partition Note: The tree defines many more partitions than the n-2 nontrivial ones constructed during the merge (or split) process. Note: For HAC methods, the merge order defines a sequence of n subtrees of the full tree. For HDC methods a sequence of subtrees can be defined if there is a figure of merit for each split.

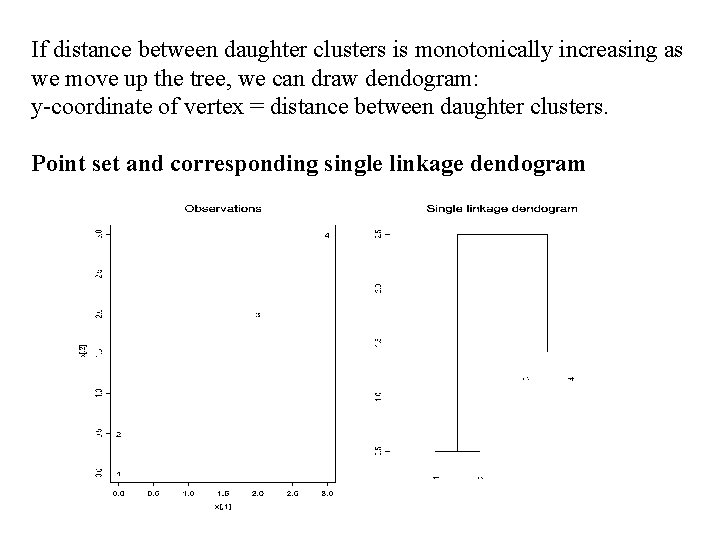
If distance between daughter clusters is monotonically increasing as we move up the tree, we can draw dendogram: y-coordinate of vertex = distance between daughter clusters. Point set and corresponding single linkage dendogram

Standard method to extract clusters from a dendogram: • Pick number of clusters k. • Cut dendogram at a level that results in k subtrees.

4. 4 Experiment Try hierarchical method on unimodal 2 D datasets. Experiments suggest: • Except in completely clear-cut situations, tree cutting (“cutree”) is useless for extracting clusters from a dendogram. • Complete linkage fails completely for elongated clusters.

Needed: • Diagnostics to decide whether the daughters of a dendogram node really correspond to spatially separated clusters. • Automatic and manual methods for dendogram pruning. • Methods for assigning observations in pruned subtrees to clusters.