4 7 Inverse Trigonometric Functions Copyright 2011 Pearson

4. 7 Inverse Trigonometric Functions Copyright © 2011 Pearson, Inc.

What you’ll learn about n n Inverse Sine Function Inverse Cosine and Tangent Functions Composing Trigonometric and Inverse Trigonometric Functions Applications of Inverse Trigonometric Functions … and why Inverse trig functions can be used to solve trigonometric equations. Copyright © 2011 Pearson, Inc. 2

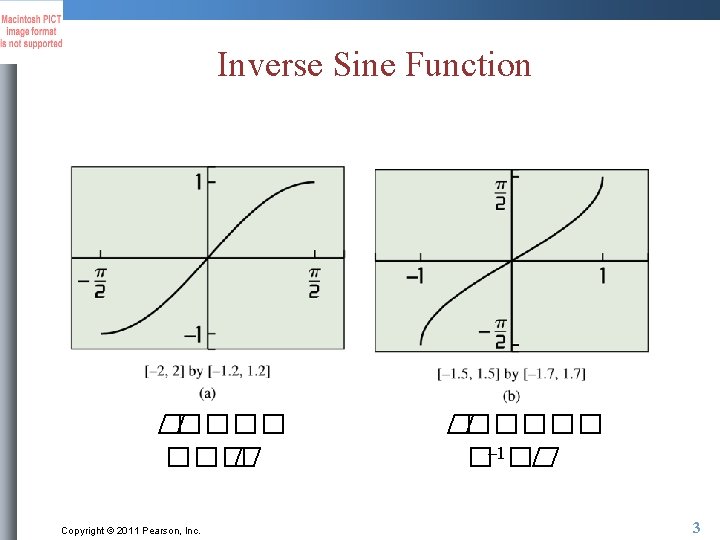
Inverse Sine Function ����� � Copyright © 2011 Pearson, Inc. ������ �– 1�� 3

Inverse Sine Function (Arcsine Function) Copyright © 2011 Pearson, Inc. 4

Example Evaluate sin– 1 x Without a Calculator Copyright © 2011 Pearson, Inc. 5

Example Evaluate sin– 1 x Without a Calculator Copyright © 2011 Pearson, Inc. 6

Example Evaluate sin-1 x Without a Calculator Copyright © 2011 Pearson, Inc. 7

Example Evaluate sin-1 x Without a Calculator Copyright © 2011 Pearson, Inc. 8

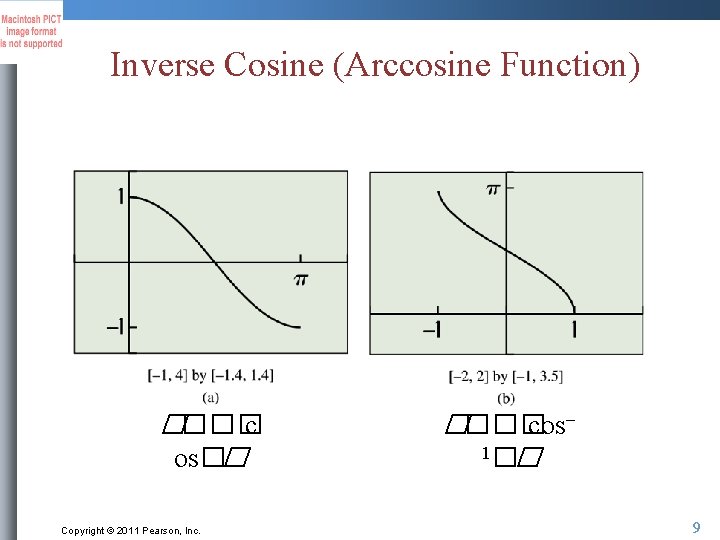
Inverse Cosine (Arccosine Function) ���� c os�� Copyright © 2011 Pearson, Inc. ���� cos– 1�� 9

Inverse Cosine (Arccosine Function) Copyright © 2011 Pearson, Inc. 10

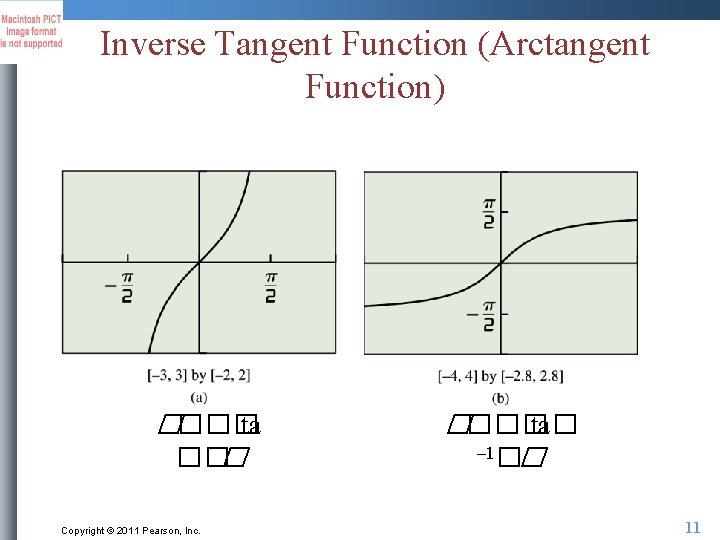
Inverse Tangent Function (Arctangent Function) ���� ta ��� Copyright © 2011 Pearson, Inc. ���� ta� – 1�� 11

Inverse Tangent Function (Arctangent Function) Copyright © 2011 Pearson, Inc. 12

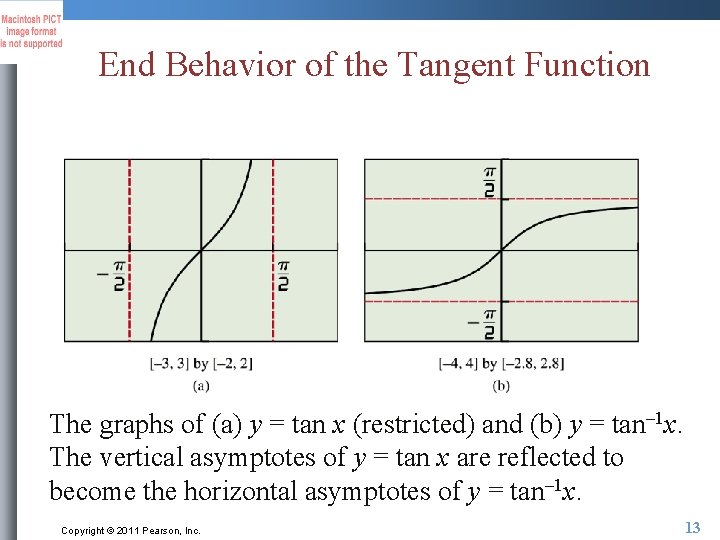
End Behavior of the Tangent Function The graphs of (a) y = tan x (restricted) and (b) y = tan– 1 x. The vertical asymptotes of y = tan x are reflected to become the horizontal asymptotes of y = tan– 1 x. Copyright © 2011 Pearson, Inc. 13

Composing Trigonometric and Inverse Trigonometric Functions Copyright © 2011 Pearson, Inc. 14

Example Composing Trig Functions with Arccosine Copyright © 2011 Pearson, Inc. 15

Example Composing Trig Functions with Arccosine ���� a triangle in which = cos – 1 x. The side opposite (which is sin ) is found by using the Pythagorean Theorem. Copyright © 2011 Pearson, Inc. 16

Example Composing Trig Functions with Arccosine Copyright © 2011 Pearson, Inc. 17

Quick Review Copyright © 2011 Pearson, Inc. 18

Quick Review Solutions Copyright © 2011 Pearson, Inc. 19