4 6 The Quadratic Formula and the Discriminant


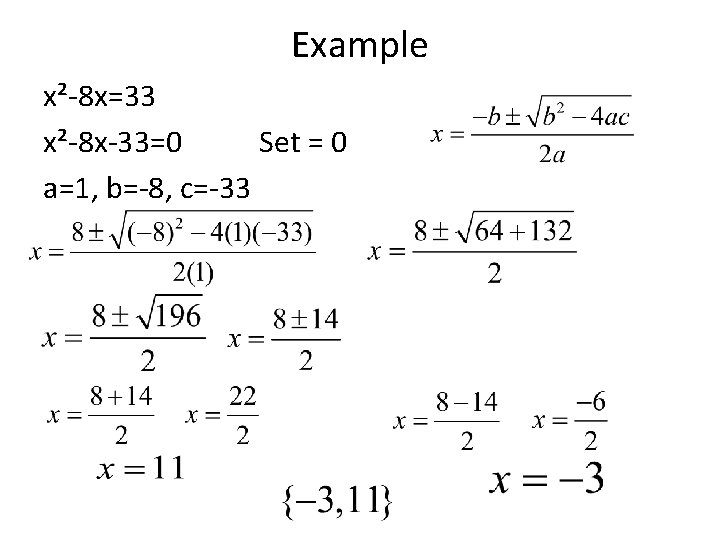



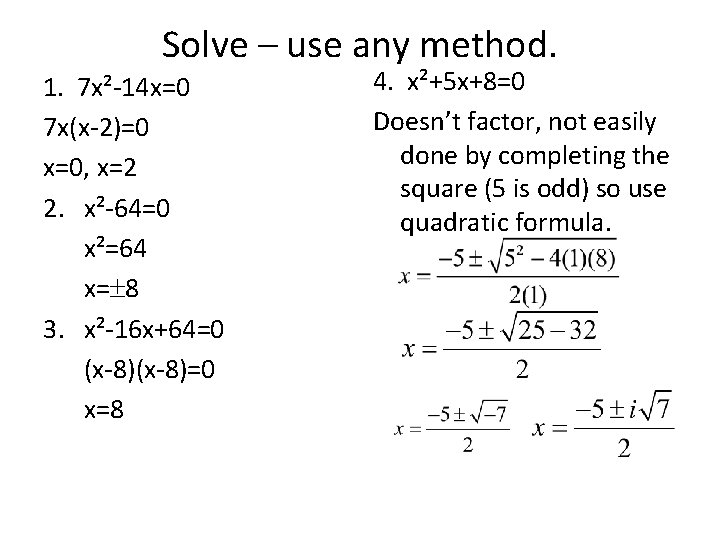

- Slides: 9

4. 6 The Quadratic Formula and the Discriminant Objectives: 1. Solve quadratic equations by using the Quadratic Formula 2. Use the discriminant to determine the number and type of roots for a quadratic equation.

Quadratic Formula Always works to solve a quadratic equation, but is a little lengthy. The solutions of a quadratic equation of the form where a≠ 0 are given by the formula:
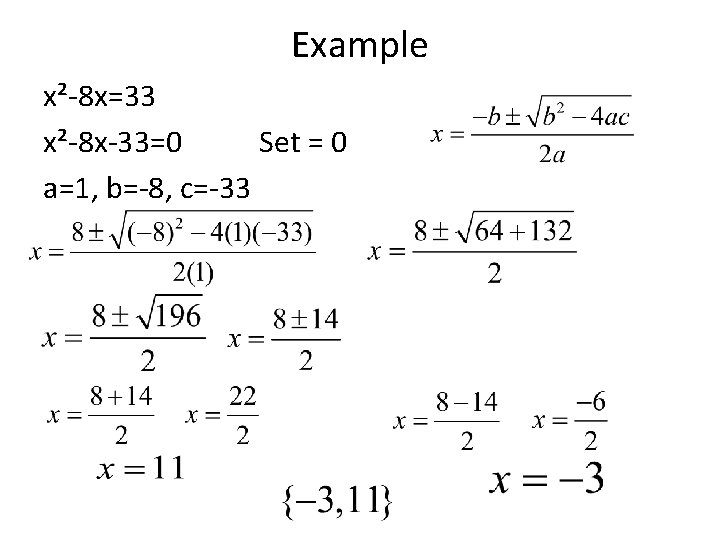
Example x²-8 x=33 x²-8 x-33=0 Set = 0 a=1, b=-8, c=-33

Another Example 7 x²+6 x+2=0 a=7, b=6, c=2 Since ALL of the coefficients are divisible by 2, simplify by dividing them by 2.

Discriminant The discriminant describes the solution to a quadratic equation. The part of the quadratic formula under the radical is the discriminant or b²-4 ac. • • If b 2 – 4 ac > 0, and a perfect square – You have two rational roots If b 2 – 4 ac >0, and not a perfect square. – You have two irrational roots If b 2 – 4 ac = 0 – You have 1 real, rational root. (Repeated root) If b 2 – 4 ac < 0 – You have two complex roots

Examples Find the discriminant and describe the number and type of roots. a. x²-16 x+64=0 b²-4 ac (-16)²-4(1)(64)= 256 -256=0 One real, rational root because the discriminant equals 0. b. 7 x²-3 x=0 (-3)²-4(7)(0)= 9 -0=9 Two rational roots because 9 is positive and a perfect square. c. 3 x²-x+5=0 (-1)²-4(3)(5)= 1 -60=-59 Two complex roots because the discriminant is a negative.

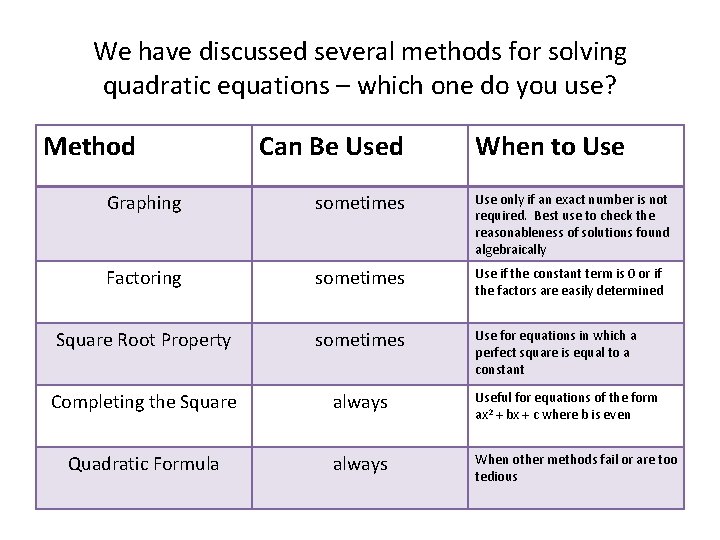
We have discussed several methods for solving quadratic equations – which one do you use? Method Can Be Used When to Use Graphing sometimes Use only if an exact number is not required. Best use to check the reasonableness of solutions found algebraically Factoring sometimes Use if the constant term is 0 or if the factors are easily determined Square Root Property sometimes Use for equations in which a perfect square is equal to a constant Completing the Square always Useful for equations of the form ax 2 + bx + c where b is even Quadratic Formula always When other methods fail or are too tedious
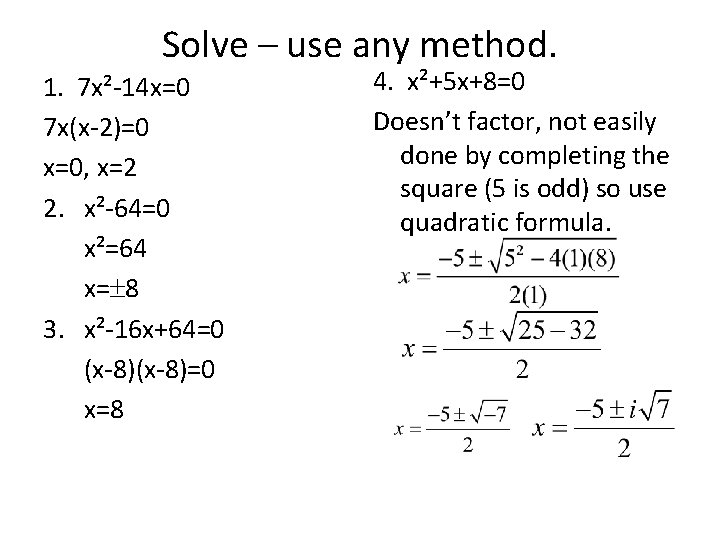
Solve – use any method. 1. 7 x²-14 x=0 7 x(x-2)=0 x=0, x=2 2. x²-64=0 x²=64 x= 8 3. x²-16 x+64=0 (x-8)=0 x=8 4. x²+5 x+8=0 Doesn’t factor, not easily done by completing the square (5 is odd) so use quadratic formula.

Homework Workbook Page 55