4 6 Rational Functions and Models Identify a












- Slides: 22

4. 6 Rational Functions and Models Identify a rational function and state its domain Identify asymptotes Interpret asymptotes Graph a rational function by using transformations ♦ Graph a rational function by hand (optional) ♦ ♦ Copyright © 2014, 2010, 2006 Pearson Education, Inc. 1

Rational Function A function f represented by where p(x) and q(x) are polynomials and q(x) ≠ 0, is a rational function. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 2

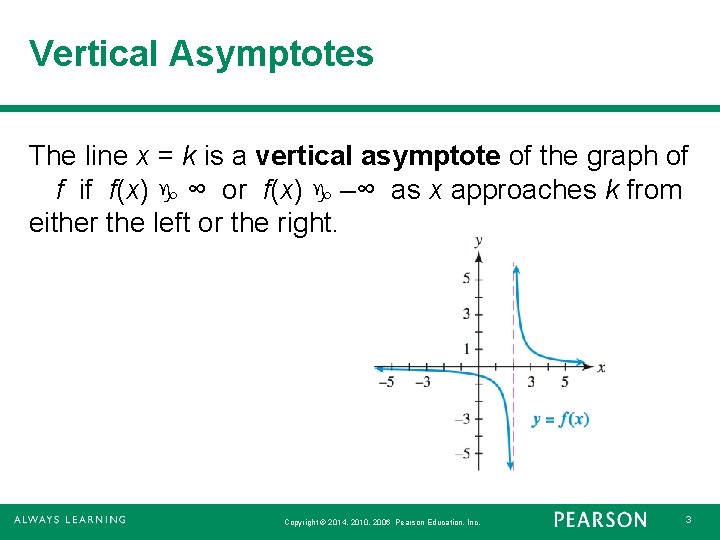
Vertical Asymptotes The line x = k is a vertical asymptote of the graph of f if f(x) g ∞ or f(x) g –∞ as x approaches k from either the left or the right. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 3

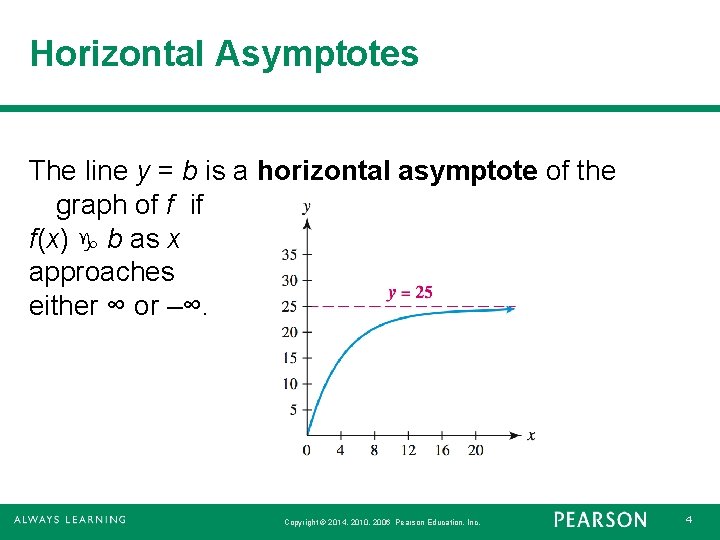
Horizontal Asymptotes The line y = b is a horizontal asymptote of the graph of f if f(x) g b as x approaches either ∞ or –∞. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 4

Finding Vertical & Horizontal Asymptotes Let f be a rational function given by written in lowest terms. Vertical Asymptote To find a vertical asymptote, set the denominator, q(x), equal to 0 and solve. If k is a zero of q(x), then x = k is a vertical asymptote. Caution: If k is a zero of both q(x) and p(x), then f(x) is not written in lowest terms, and x – k is a common factor. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 5

Finding Vertical & Horizontal Asymptotes Horizontal Asymptote (a) If n<m the degree of the numerator is less than the degree of the denominator, then y = 0 (the x-axis) is a horizontal asymptote. (b) If n=m the degree of the numerator equals the degree of the denominator, then y = a/b is a horizontal asymptote, where a is the leading coefficient of the numerator and b is the leading coefficient of the denominator. (c) If n>m the degree of the numerator is greater than the degree of the denominator, then there are no horizontal asymptotes. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 6

Teaching Example 1 Determine if the function is rational and state its domain. (b) (a) Solution (a) Both the numerator and the denominator are polynomials, so the function is rational. Since (b) the domain is The numerator is not a polynomial, so the function is not rational. Since the domain is all real numbers. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 7

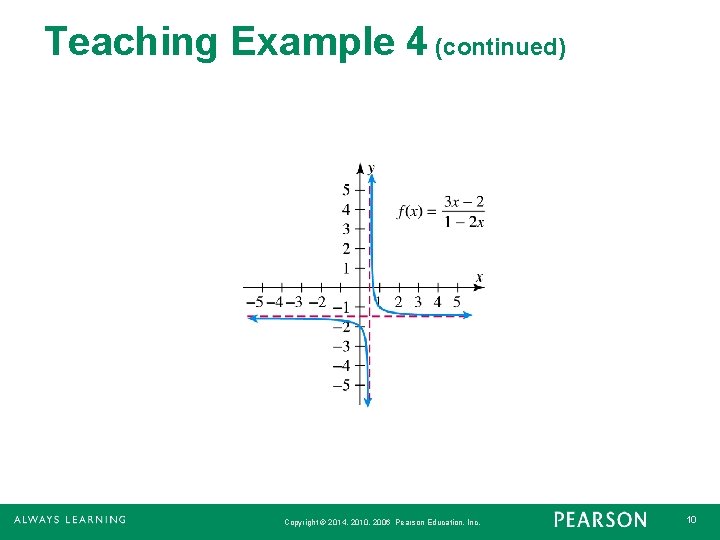
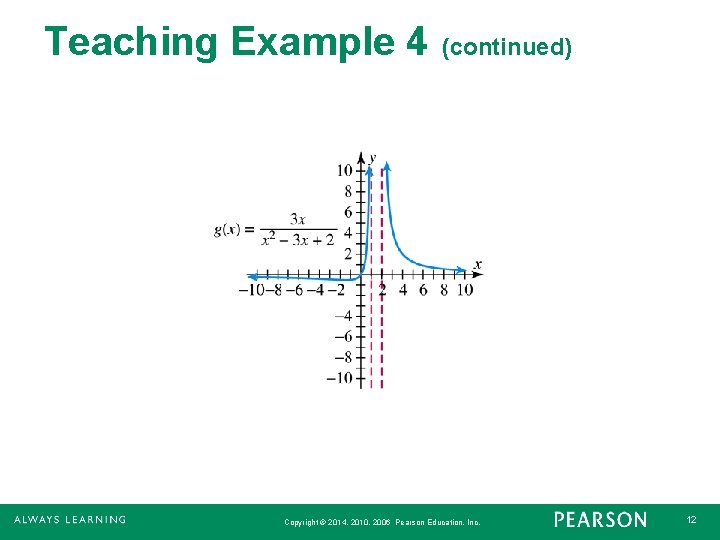
Teaching Example 4 Determine any horizontal or vertical asymptotes for each rational function. (a) (b) (c) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 8

Teaching Example 4 (continued) Solution (a) Since the degrees of the numerator and the denominator are both 1, and the ratio of the leading coefficients is asymptote is , the horizontal To find the vertical asymptote, solve 1 − 2 x = 0. is the vertical asymptote. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 9

Teaching Example 4 (continued) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 10

Teaching Example 4 (continued) (b) The degree of the numerator is one less than the degree of the denominator, so the x-axis (y = 0) is the horizontal asymptote. To find the vertical asymptotes, solve are the vertical asymptotes. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 11

Teaching Example 4 (continued) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 12

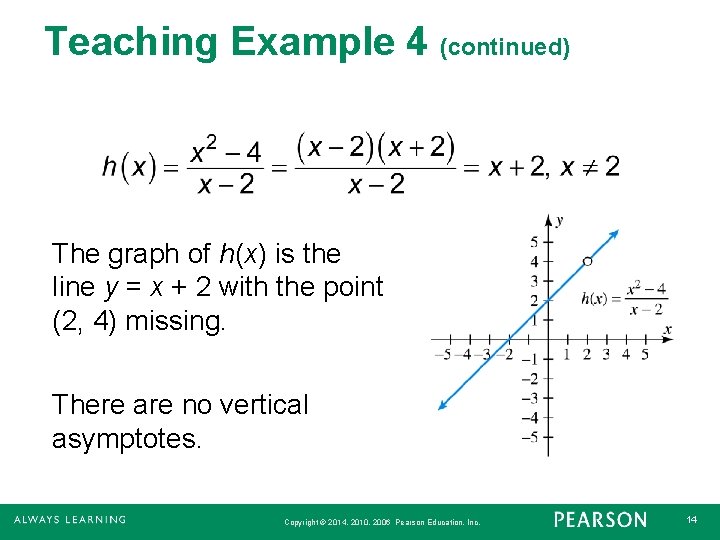
Teaching Example 4 (continued) (c) The degree of the numerator is greater than the degree of the denominator, so there are no horizontal asymptotes. When x = 2, both numerator and denominator equal 0, so the expression is not in lowest terms. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 13

Teaching Example 4 (continued) The graph of h(x) is the line y = x + 2 with the point (2, 4) missing. There are no vertical asymptotes. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 14

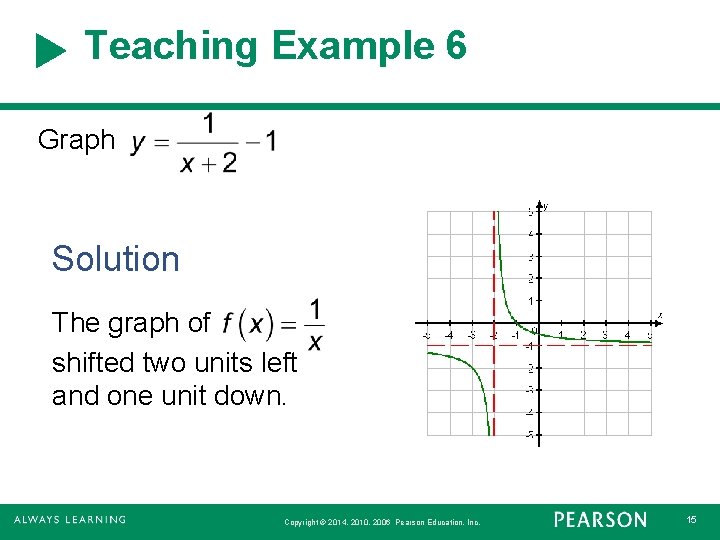
Teaching Example 6 Graph Solution The graph of shifted two units left and one unit down. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 15

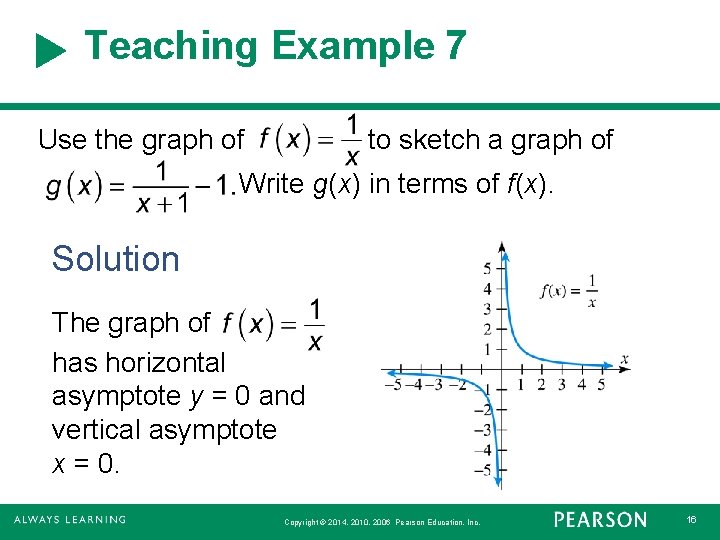
Teaching Example 7 Use the graph of to sketch a graph of Write g(x) in terms of f(x). Solution The graph of has horizontal asymptote y = 0 and vertical asymptote x = 0. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 16

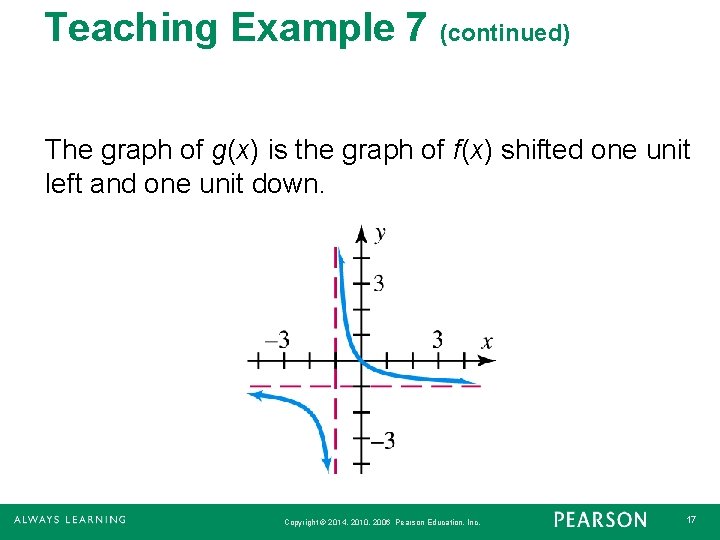
Teaching Example 7 (continued) The graph of g(x) is the graph of f(x) shifted one unit left and one unit down. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 17

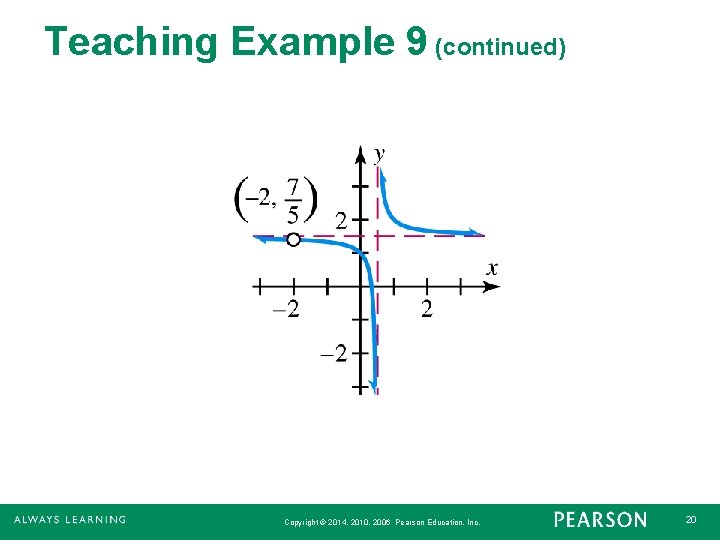
Teaching Example 9 Solution Since the degrees of the numerator and the denominator are the same, and the ratio of the leading coefficients is , the horizontal asymptote is Copyright © 2014, 2010, 2006 Pearson Education, Inc. 18

Teaching Example 9 (continued) When x = − 2, both numerator and denominator equal 0, so the expression is not in lowest terms. is the horizontal asymptote. Since x ≠ − 2, there is a hole in the graph at Copyright © 2014, 2010, 2006 Pearson Education, Inc. 19

Teaching Example 9 (continued) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 20

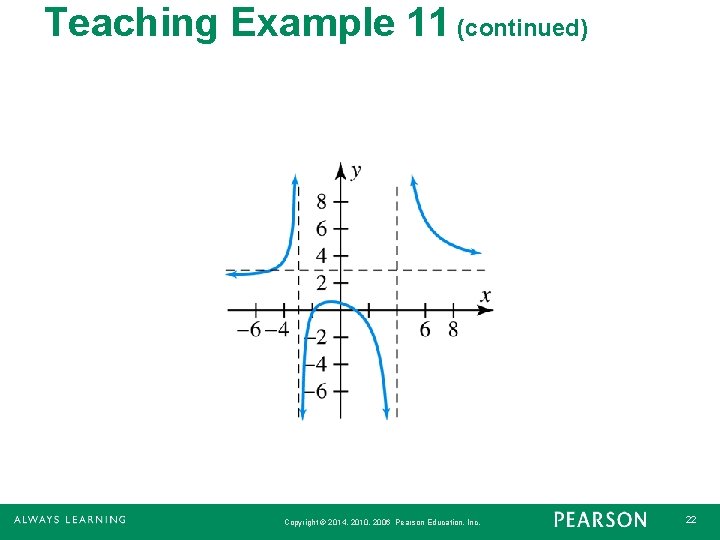
Teaching Example 11 Use these steps to graph this polynomial by hand: 1. Make the function is rational and in simplest form. 2. Find any Asymptotes (Vertical, Horizontal or Oblique) 3. Find y-intercept (if any) 4. Find x-intercept (if any) 5. Determine if the graph will intersect the H. A. (or oblique) 6. Plot selected points 7. Complete the graph. Copyright © 2014, 2010, 2006 Pearson Education, Inc. 21

Teaching Example 11 (continued) Copyright © 2014, 2010, 2006 Pearson Education, Inc. 22