4 4 Prove Triangles Congruent by HL Geometry

4. 4 – Prove Triangles Congruent by HL Geometry Ms. Rinaldi

Right Triangles In a right triangle, the sides next to the right angle are called the legs. The side opposite the right angle is called the hypotenuse. leg hypotenuse leg

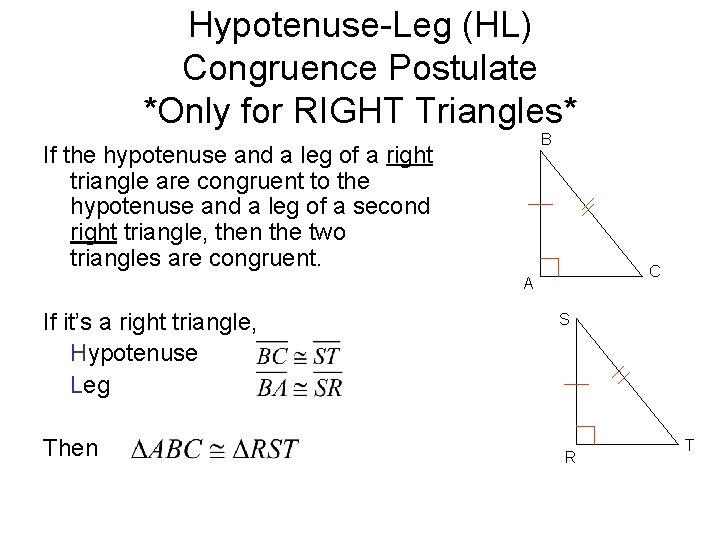
Hypotenuse-Leg (HL) Congruence Postulate *Only for RIGHT Triangles* B If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of a second right triangle, then the two triangles are congruent. C A If it’s a right triangle, Hypotenuse Leg Then S R T

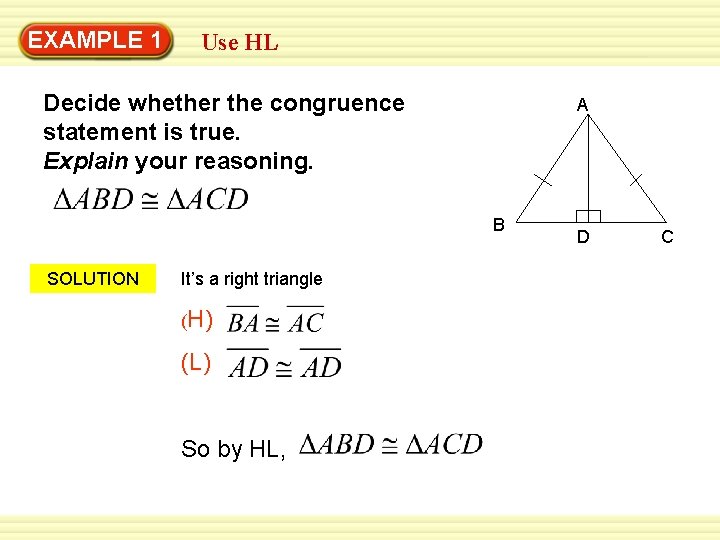
EXAMPLE 1 Use HL Decide whether the congruence statement is true. Explain your reasoning. A B SOLUTION It’s a right triangle (H) (L) So by HL, D C

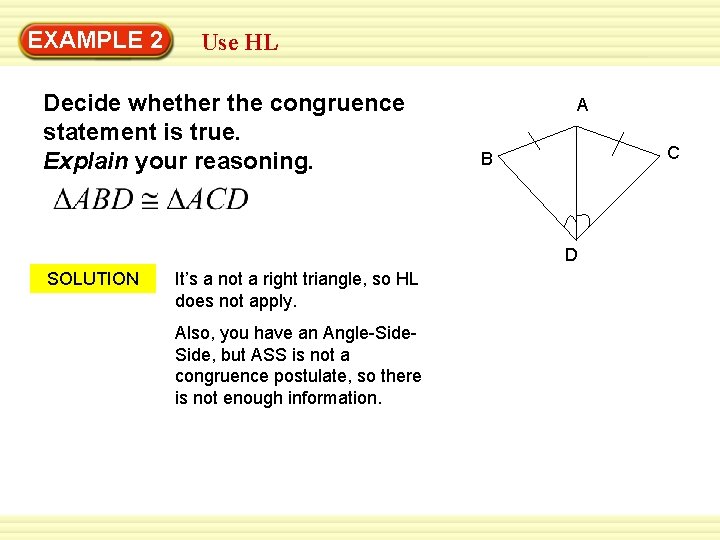
EXAMPLE 2 Use HL Decide whether the congruence statement is true. Explain your reasoning. A C B D SOLUTION It’s a not a right triangle, so HL does not apply. Also, you have an Angle-Side, but ASS is not a congruence postulate, so there is not enough information.

EXAMPLE 3 Use HL Decide whether the congruence statement is true. Explain your reasoning.

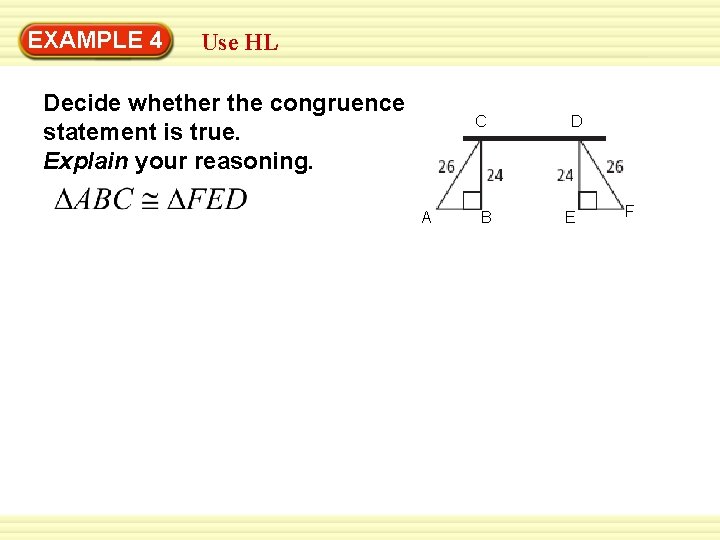
EXAMPLE 4 Use HL Decide whether the congruence statement is true. Explain your reasoning. C A B D E F

EXAMPLE 5 Use HL State third congruence that must be given to prove that using the indicated postulate. B Given: Angle A and D are right angles. Use the HL Congruence Postulate. A C E F D