4 4 Congruence and Transformations On Geogebra construct

4. 4 Congruence and Transformations

On Geogebra, construct a scalene triangle using the polygon tool (5 th from left, top of list). Construct a line (3 rd from left, top of list) not through the triangle. Reflect the triangle about that line. Construct a second line parallel (4 th from left, 2 nd on list) to the first line. Reflect the second triangle about the second line. Draw a line from each vertex of the original triangle perpendicular to (4 th from left, top of list) the line of reflection. Is there a single transformation that maps the first triangle to the third? Make a conjecture.

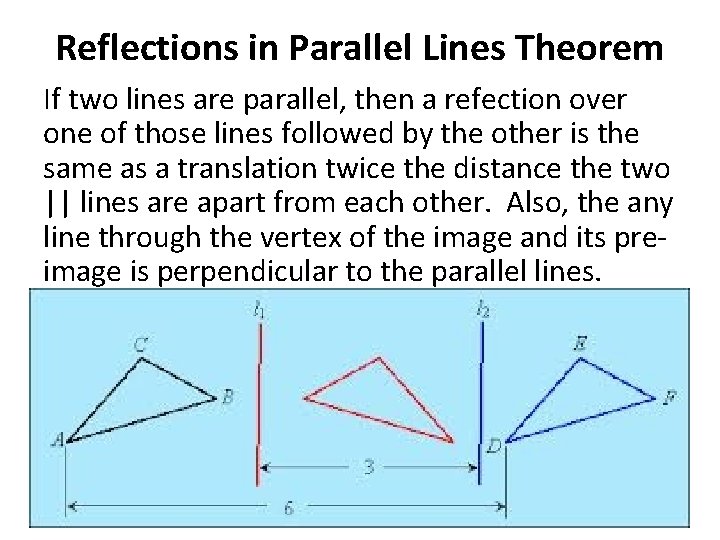
Reflections in Parallel Lines Theorem If two lines are parallel, then a refection over one of those lines followed by the other is the same as a translation twice the distance the two || lines are apart from each other. Also, the any line through the vertex of the image and its preimage is perpendicular to the parallel lines.

Start with a new scalene triangle. Draw any line and reflect the triangle about it. Draw a new line so that the two lines form an angle 90 degrees or less. Reflect the second triangle about the second line. Find the measure of the angle created by the two lines of reflection. Rotate the original triangle towards the third triangle the same angle measure created by the two lines of reflection TWICE. Make a conjecture about reflecting a figure about two intersecting lines.

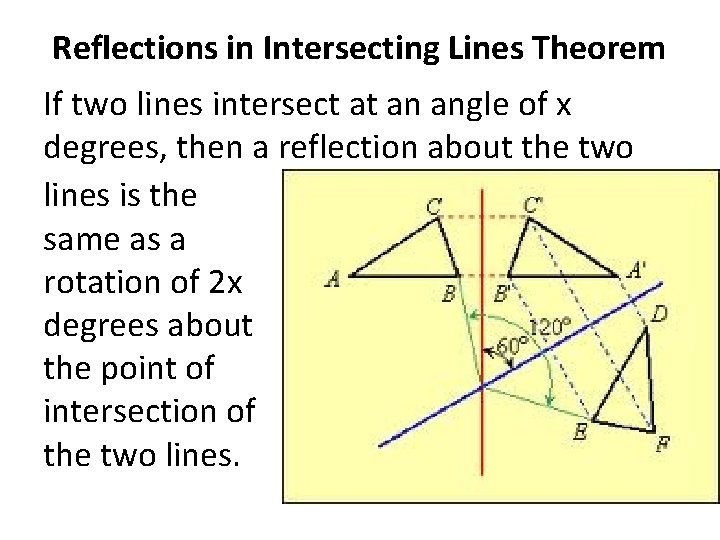
Reflections in Intersecting Lines Theorem If two lines intersect at an angle of x degrees, then a reflection about the two lines is the same as a rotation of 2 x degrees about the point of intersection of the two lines.

Congruence Transformation • A rigid motion or combination of rigid motions where the pre-image and image are congruent. The terms “rigid motion” and “congruence transformation” are interchangeable. The antonym to rigid motion would be a dilation.

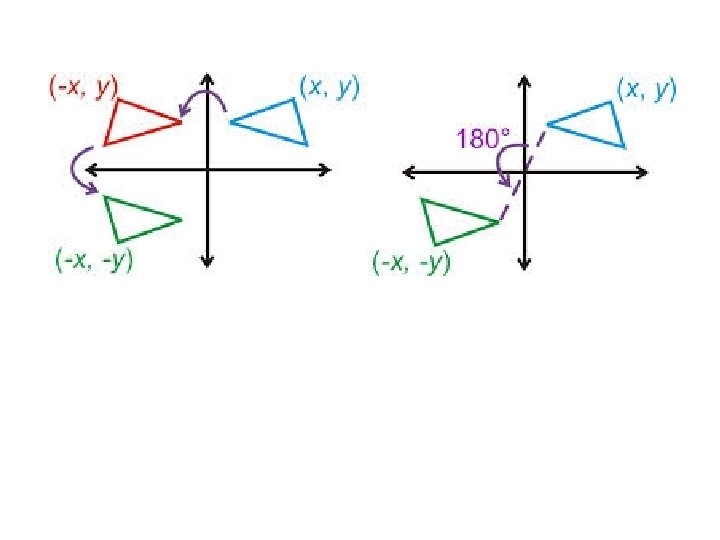
Describe the congruence transformation that maps ABC to A’’B’’C’’

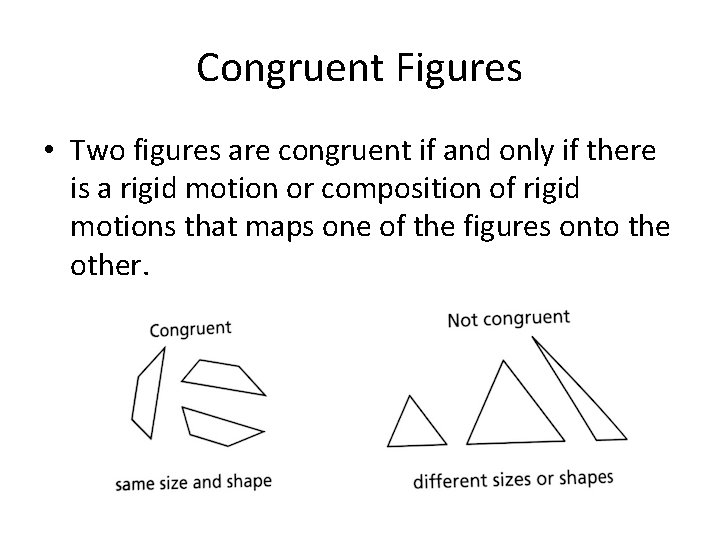
Congruent Figures • Two figures are congruent if and only if there is a rigid motion or composition of rigid motions that maps one of the figures onto the other.

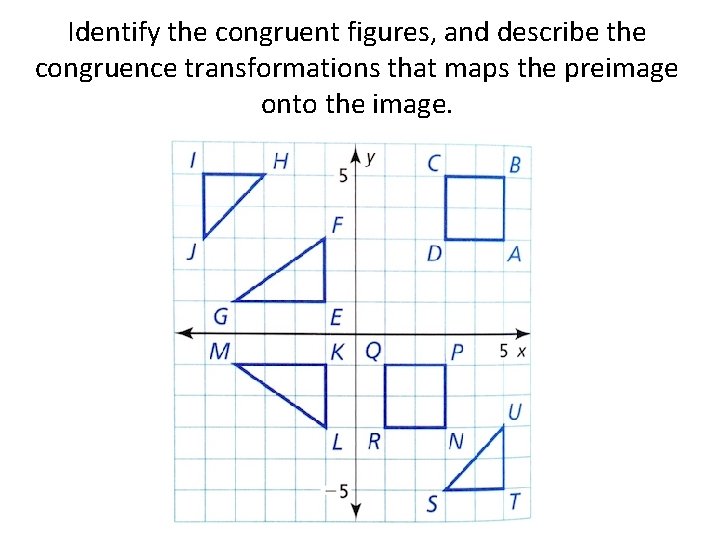
Identify the congruent figures, and describe the congruence transformations that maps the preimage onto the image.