4 3 WRITING FUNCTIONS Objectives Identify independent and

4. 3 WRITING FUNCTIONS Objectives Identify independent and dependent variables. Write an equation in function notation and evaluate a function for given input values. Vocabulary independent variable function rule function notation

Example 1: Using a Table to Write an Equation Determine a relationship between the x- and y-values. Write an equation. x 5 10 15 20 y 1 2 3 4 How do we go from 5 to 1? method works for all x and y? Equation Does equation represent a function?

The input of a function is the independent variable. The output of a function is the dependent variable. The value of the dependent variable depends on, or is a function of, the value of the independent variable. Example 2 A: Identifying Independent and Dependent Variables Identify the independent and dependent variables in the situation. A painter must measure a room before deciding how much paint to buy. What are our two variables? Then complete the sentence: The depends on the Dependent: Independent: The height of a candle decrease d centimeters for every hour it burns.

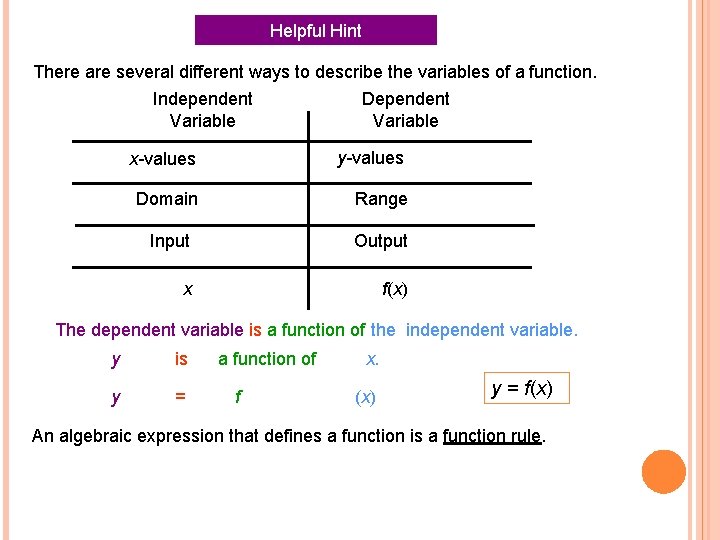
Helpful Hint There are several different ways to describe the variables of a function. Independent Variable Dependent Variable x-values y-values Domain Range Input Output x f(x) The dependent variable is a function of the independent variable. y is y = a function of f x. (x) y = f(x) An algebraic expression that defines a function is a function rule.

Example 3 A: Writing Functions Identify the independent and dependent variables. Write a rule in function notation for the situation. A math tutor charges $35 per hour. Variables? Dependent: Independent: The depends on Let h represent the number of hours of tutoring. The function rule for the amount a math tutor charges is f(h) = 35 h.

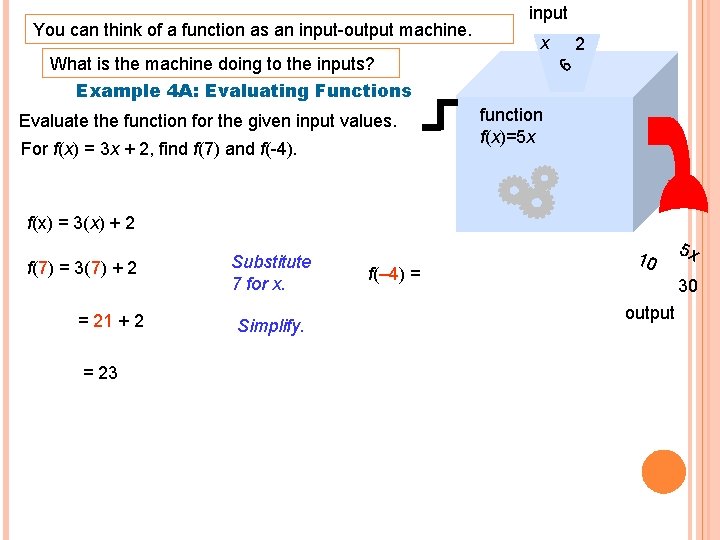
You can think of a function as an input-output machine. input x What is the machine doing to the inputs? 2 6 Example 4 A: Evaluating Functions Evaluate the function for the given input values. For f(x) = 3 x + 2, find f(7) and f(-4). function f(x)=5 x f(x) = 3(x) + 2 f(7) = 3(7) + 2 = 21 + 2 = 23 Substitute 7 for x. Simplify. f(– 4) = 10 5 x 30 output

Example 5: Finding the Reasonable Range and Domain of a Function Joe has enough money to buy 1, 2, or 3 DVDs at $15. 00 each. Write a function to describe the situation. Find a reasonable domain and range of the function. How many DVDs will Joe buy? So what are our variable? Money spent f(x) is = $15. 00 for each • DVD. x If Joe buys x DVDs, he will spend f(x) = 15 x dollars. Joe only has enough money to purchase 1, 2, or 3 DVDs. A reasonable domain is {1, 2, 3}. Could 1. 5 be one of the x-values in the domain? What is the range? 1 3 2 x f(x) 15(1) = 15 15(2) = 30 15(3) = 45