4 3 Riemann Sums and Definite Integrals Objectives

4. 3 Riemann Sums and Definite Integrals

Objectives • Understand the definition of a Riemann sum. • Evaluate a definite integral using limits. • Evaluate a definite integral using properties of definite integrals.

Riemann Sums When we find the area under a curve by adding rectangles, the answer is called a Riemann sum. The width of a rectangle is called a subinterval The entire interval is called the partition Subintervals do not all have to be the same size.

Riemann Sums: • Add areas of rectangles to estimate area. • Rectangle widths don’t have to be the same. • 3 basic types: – Left (use f(left endpoint) as height) – Right (use f(right endpoint) as height) – Midpoint (use f(midpoint) as height)

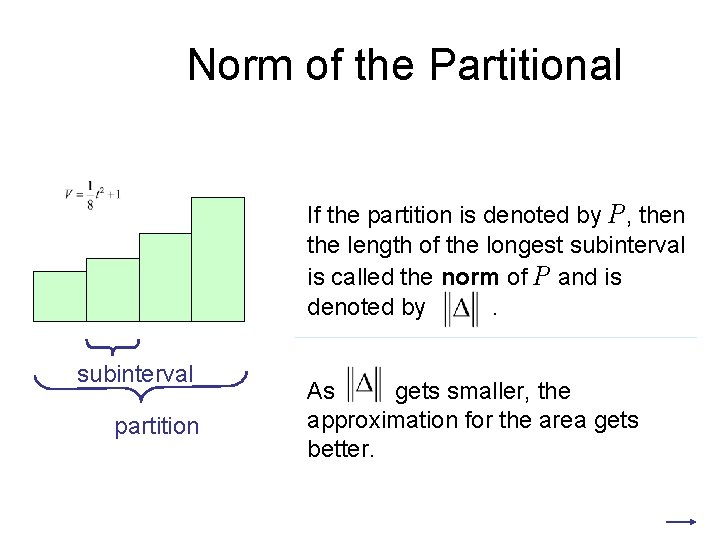
Norm of the Partitional If the partition is denoted by P, then the length of the longest subinterval is called the norm of P and is denoted by. subinterval partition As gets smaller, the approximation for the area gets better.

Definition of a Definite Integral If f is defined on [a, b] and the limit exists then f is integrable on [a, b] and the limit is denoted by discrete Longest rectangle width 0 # rectangles ∞ continuous

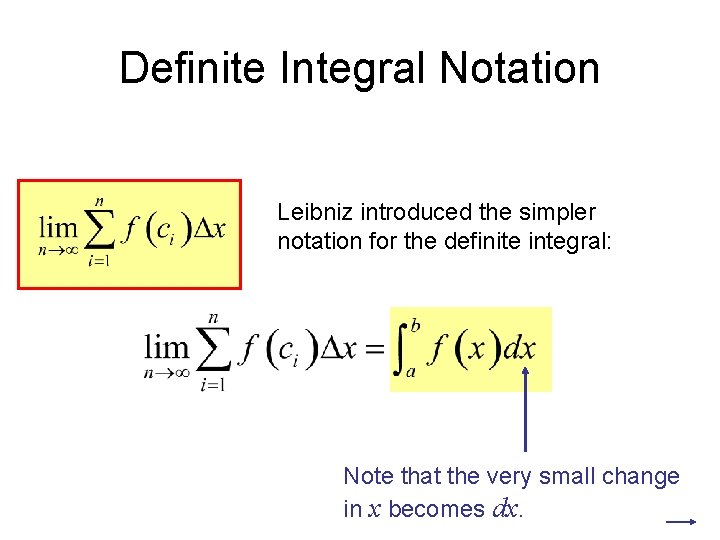
Definite Integral Notation Leibniz introduced the simpler notation for the definite integral: Note that the very small change in x becomes dx.

Theorem 4. 4: Continuity Implies Integrability If a function f is continuous of [a, b], then f is integrable on [a, b].

Example Evaluate the definite integral Remember: Why is it negative?

Theorem If f is continuous and nonnegative on [a, b], then the area of the region bounded by the graph of f, the x-axis, and the vertical lines x=a and x=b is given by

Example Consider the region bounded by the graph of f(x)=4 x-x 2 and the x-axis.

Example Sketch the region corresponding to each definite integral, then evaluate each integral using a geometric formula.

Properties of Definite Integrals

More Properties

Homework 4. 3 (page 278) # 13 – 43 odd 47, 53