4 3 Prove Triangles Congruent by SSS Geometry

4. 3 – Prove Triangles Congruent by SSS Geometry Ms. Rinaldi

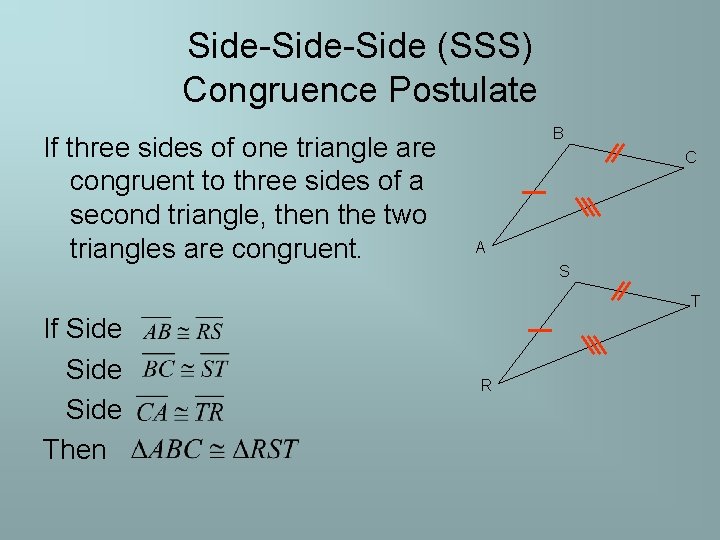
Side-Side (SSS) Congruence Postulate If three sides of one triangle are congruent to three sides of a second triangle, then the two triangles are congruent. B C A S T If Side Then R

EXAMPLE 1 Use the SSS Congruence Postulate Decide whether the congruence statement is true. Explain your reasoning. SOLUTION Given Reflexive Property So, by the SSS Congruence Postulate,

EXAMPLE 2 Use the SSS Congruence Postulate Decide whether the congruence statement is true. Explain your reasoning. ACB SOLUTION CAD It is given that BC AD By Reflexive property AC AC, But AB is not congruent CD. Therefore, the triangles are not congruent.

EXAMPLE 3 Use the SSS Congruence Postulate Decide whether the congruence statement is true. Explain your reasoning. DFG HJK

EXAMPLE 4 Use the SSS Congruence Postulate Decide whether the congruence statement is true. Explain your reasoning. A D B C

EXAMPLE 5 Use the SSS Congruence Postulate Decide whether the congruence statement is true. A Explain your reasoning. B C D

EXAMPLE 6 Use the SSS Congruence Postulate has vertices J(-3, -2), K(0, -2), and L(-3, -8). has vertices R(10, 0), S(10, -3), and T(4, 0). Graph the triangles in the same coordinate plane and show that they are congruent. SOLUTION Use the distance formula to find the lengths of the diagonal segments. LK = TS =6. 7 (By distance formula) KJ = SR = 3. (By counting) JL = RT = 6. (By counting) Therefore, by SSS, the triangles are congruent.

EXAMPLE 7 Use the SSS Congruence Postulate has vertices P(-5, 4), Q(-1, 4), and R(-1, 1). has vertices A(2, 5), B(2, 1), and C(5, 1). Graph the triangles in the same coordinate plane and show that they are congruent. STEP 1: Graph STEP 2: Use the distance formula to find the lengths of the diagonal segments. PR = AC = PR = _____ =______ (By _______) PQ =_____ = _____ (By_______) QR = _____ (By ______) Therefore, by ______, _____________.