4 3 Graphing Quadratic Equations and its Transformations

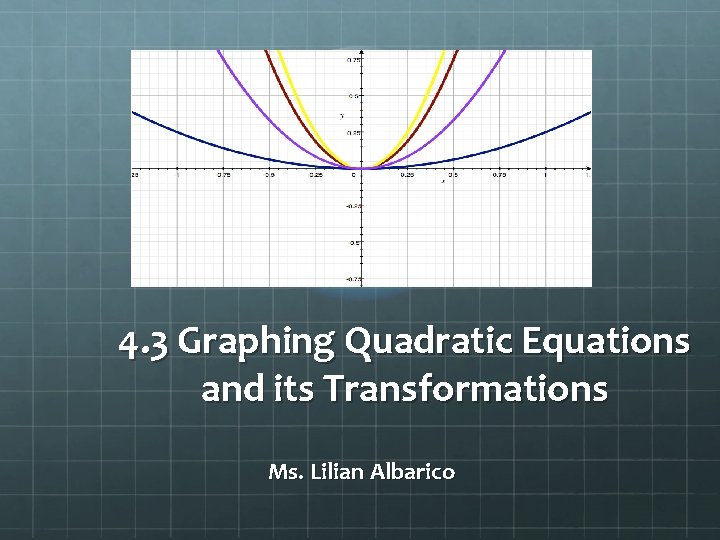
4. 3 Graphing Quadratic Equations and its Transformations Ms. Lilian Albarico

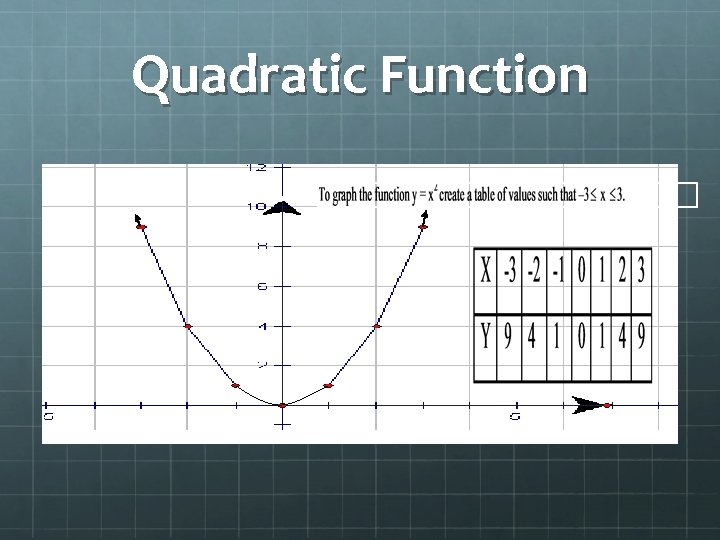
Quadratic Function The graph produced by y = x 2 is a curve called a parabola. The parabola is a symmetrical curve that has one axis of symmetry. The axis of symmetry is a vertical line that passes through the turning point of the parabola. The turning point is called the vertex. The equation of the axis of symmetry is x = the value of the x co-ordinate of the vertex. Every parabola that is graphed is this standard curve with transformations performed on it.

Quadratic Function y x

Transformations: Vertical Reflection (Reflection in the x-axis) Vertical Stretch Vertical Translation/Shift Horizontal Translation/Shift

Key Terms: Mapping notation – a notation that describes how a graph and its image are related x 2 -------> (x, y) reflection in x-axis – a transformation that vertically flips the graph of a curve in the x-axis vertical stretch – a transformation that describes how the y-values of a curve are stretched by a scale factor vertical translation – a transformation that describes the number of units and the direction that a curve moves vertically from the origin horizontal translation – a transformation that describes the number of units and the direction that a curve moves horizontally from the origin

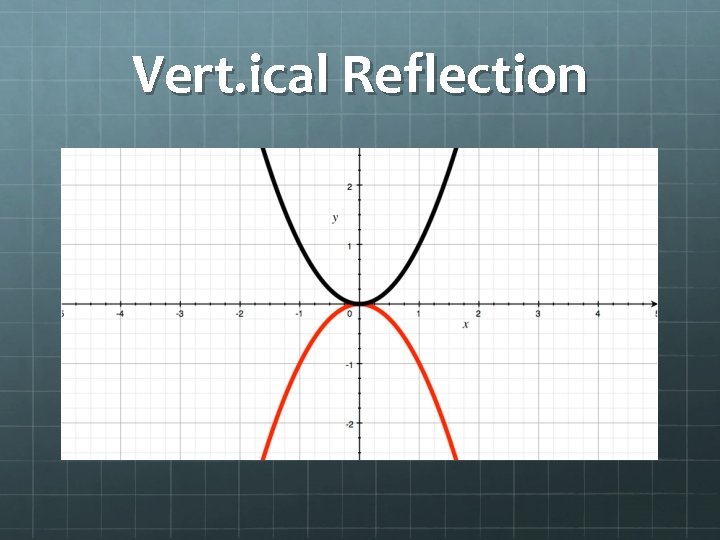
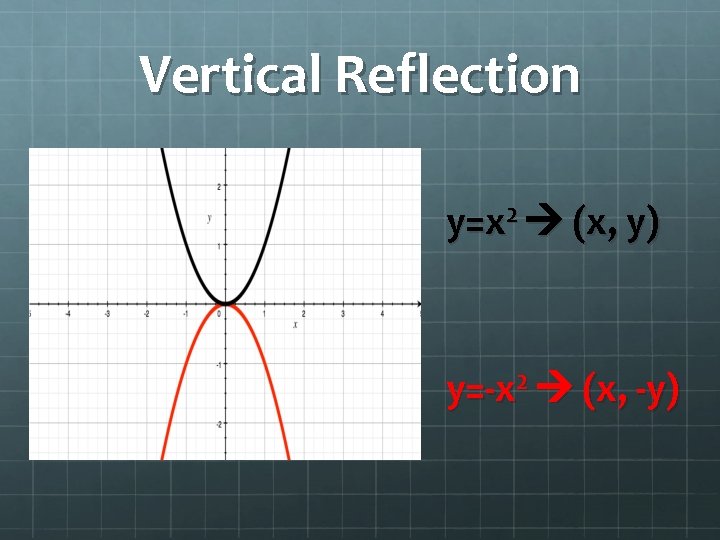
Vertical Reflection (V. R. ) – a transformation in which a plane figure flips over vertically and has a horizontal axis of reflection. Also called as Reflection in x-axis.

Vert. ical Reflection

Vertical Reflection y=x 2 (x, y) y=-x 2 (x, -y)

Vertical Reflection Draw the following quadratic equations, then write the mapping notations and include a table with 5 values: 1) f(x) = x 2 and -f(x) = x 2 2) f(x) = 4 x 2 and -f(x) = 4 x 2 3) f(x) = 1/4 x 2 and - f(x) = 1/4 x 2

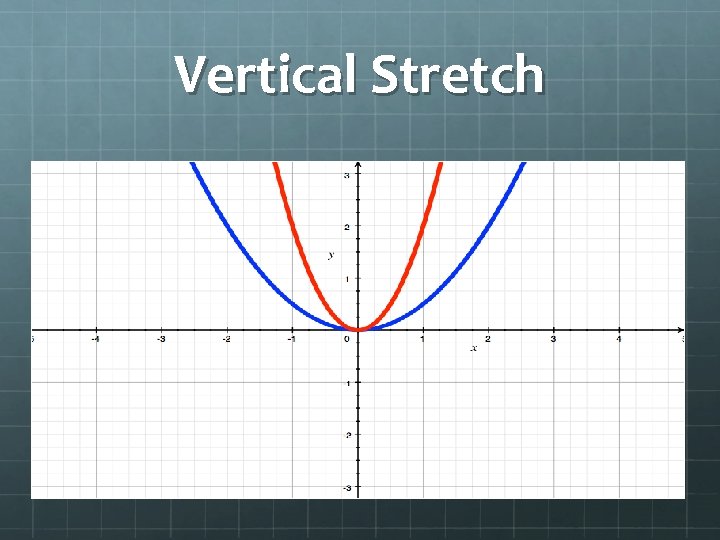
Vertical Stretch (V. S. ) – a transformation that describes how the y – value is stretched by a scale factor (the number times y)

Vertical Stretch

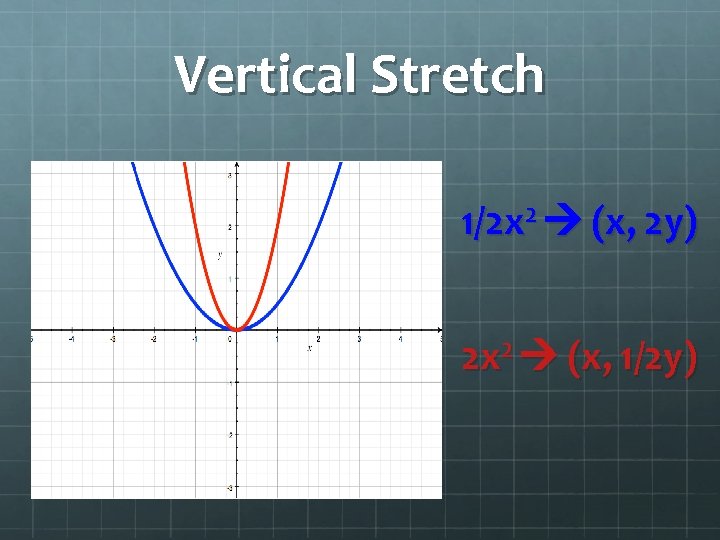
Vertical Stretch 1/2 x 2 (x, 2 y) 2 x 2 (x, 1/2 y)

Vertical Stretch Draw the following quadratic equations, then write the mapping notation and include a table with 5 data values: 1) f(x) = x 2 2 y = x 2 1/3 y= x 2 2) 3 y = x 2 4 y= x 2 1/4 y = x 2 3/4 y = x 2

Homework CYU # 5 on page 175 CYU # 8, 9, 10, 11 , 12 , and 13 on pages 177 -178.

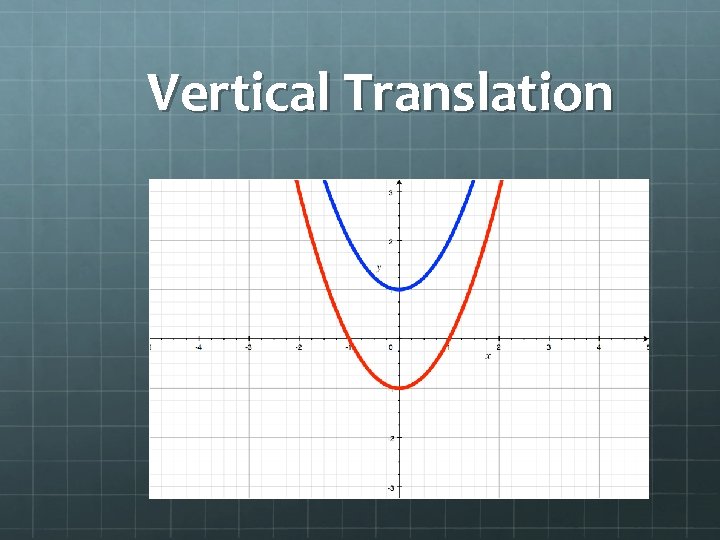
Vertical Translation (V. T. ) - a transformation that describes the number of units and direction that a curve has moved vertically.

Vertical Translation

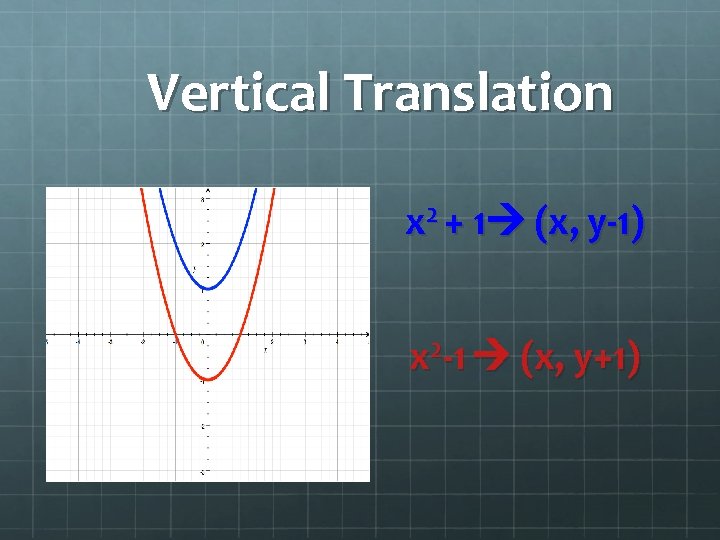
Vertical Translation x 2 + 1 (x, y-1) x 2 -1 (x, y+1)

Vertical Translation Draw the following quadratic equations, then write the mapping notation and include a table with 5 data values: 1) y = x 2 y + 2 = x 2 y-2 = x 2 2) y-3 = x 2 (y+3)= -x 2 y-1/2 = x 2 y+1/2 = 2 x 2

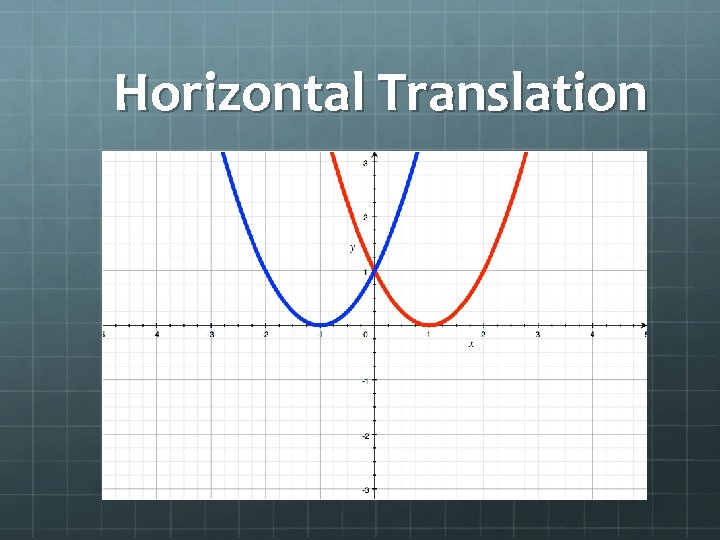
Horizontal Translation (H. T. ) – a transformation that describes the number of units and direction that a curve has moved horizontally.

Horizontal Translation

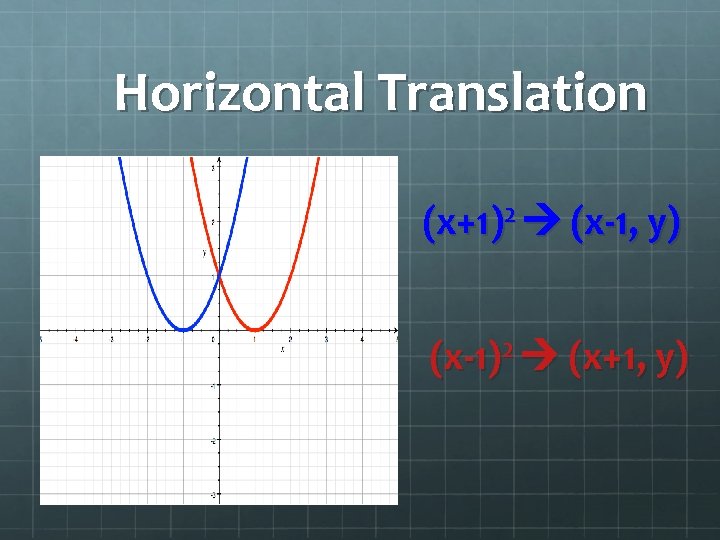
Horizontal Translation (x+1)2 (x-1, y) (x-1)2 (x+1, y)

Horizontal Translation Draw the following quadratic equations, then write the mapping notation and include a table with 5 data values: 1) y = x 2 y = (x+3)2 y = (x-4)2 2) y = 2(x+3)2 -y= (x-2)2 2 y = (x-2)2 y-1 = (x+1)2

HOMEWORK CYU #14 AND 14 ON PAGE 179 CYU # 18, 20, 21, 22, and 23 on page 181 – 182.

SUMMARY

Learning Check: When you see a –y in the equation the image is a _________ in the x-axis. “When I see a 3 y in the equation, then I know that there is a vertical stretch of ______. ” The vertical stretch factor is the _____ of the coefficient of y. “When I see y+2 in the equation, then I know that there is vertical translation of ____ units _____”. “When I see y-3 in the equation, then I know that there is vertical translation of ____ units _____”. The vertical translation is the ______of the number being added to the y. “When I see x+3 in the equation, then I know that there is horizontal translation by ____ units to the _____”. “When I see x-4 in the equation, then I know that there is horizontal translation by ____ units to the _____”. The horizontal translation is the ______ of the number being added to the x. ”

Let’s combine all transformations!

1) Graph the following quadratic functions and write down their mapping notations: -y = (x+2)2 -2 y = (x-1)2 y = (x-3)2

2) Based from the mapping notation below, write the quadratic equation and the draw its graph transformation: (x , y) (x+2, y) (x, y) (x+6, y-1) (x, y) (x-1/2, y – 3/2) (x, y) (x-2, -2 y)

Absolute Value Functions

Absolute Value Functions absolute value – the absolute value of a number is the number without its sign |n| = n, |-n| = n. If absolute value is related to a number line, then it indicates the measure of the distance between a point and its origin without reference to direction. Absolute value functions are graphed using y = |x| after the transformations have been applied.

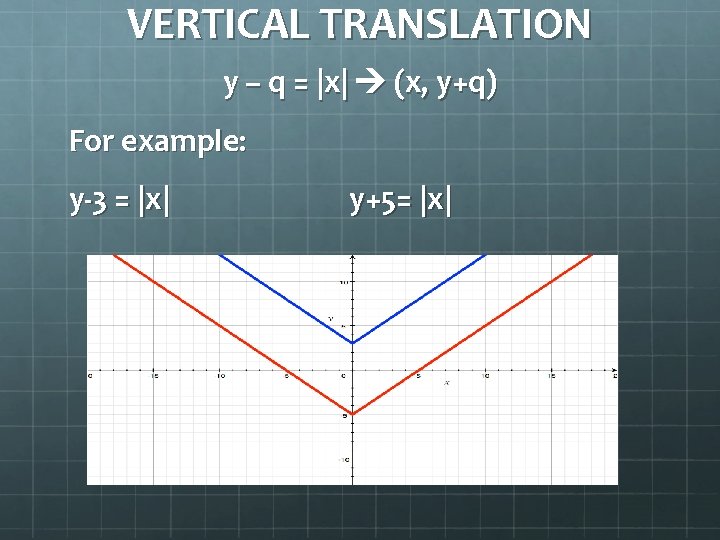
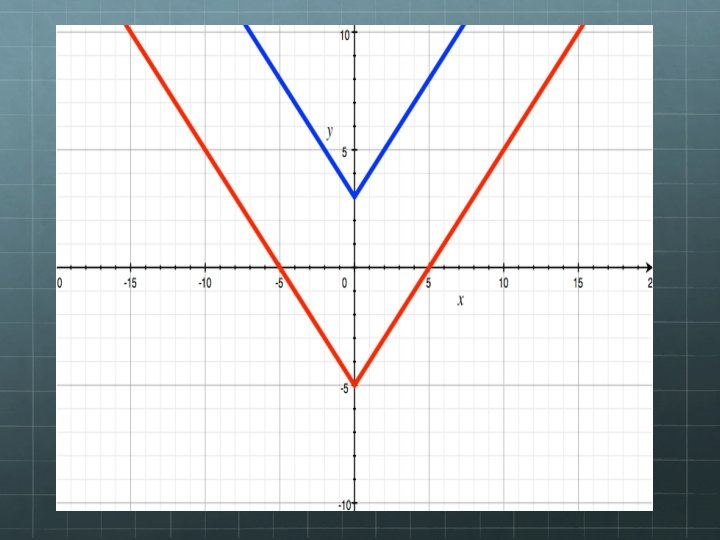
VERTICAL TRANSLATION y – q = |x| (x, y+q) For example: y-3 = |x| y+5= |x|

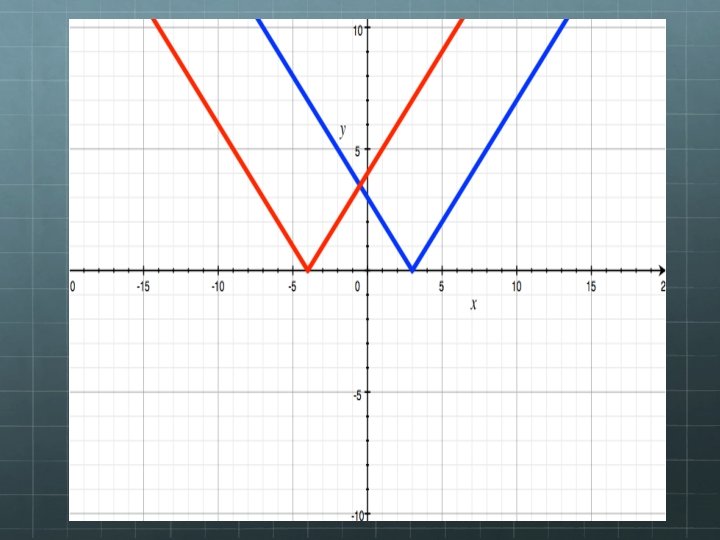
HORIZONTAL TRANSLATION y = |x-p| (x+p, y) For example: y = |x-3| y= |x+4|

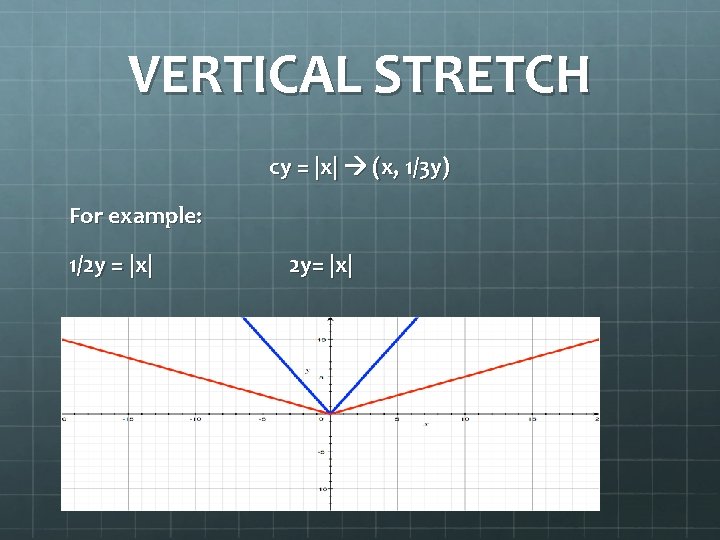
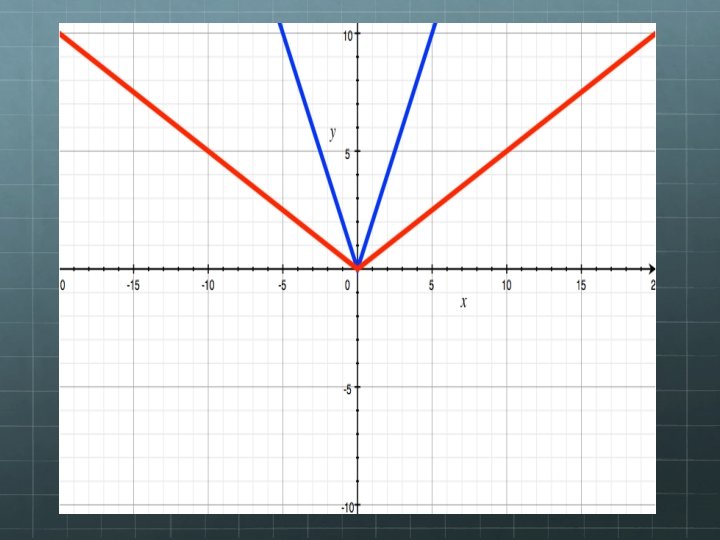
VERTICAL STRETCH cy = |x| (x, 1/3 y) For example: 1/2 y = |x| 2 y= |x|

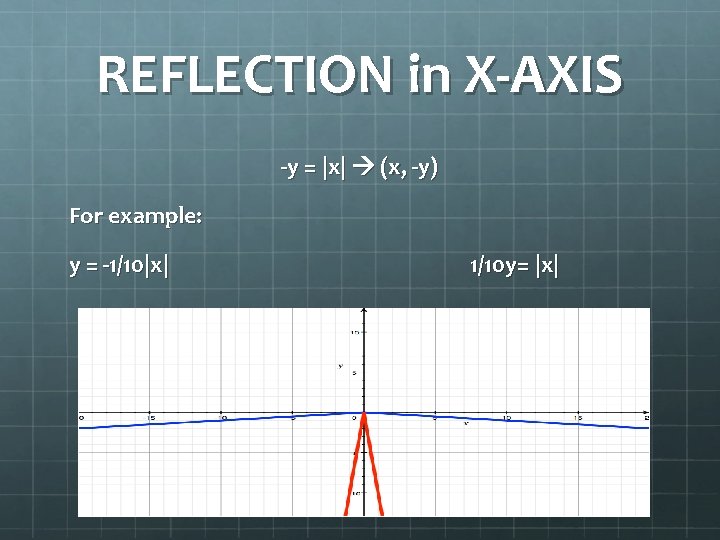
REFLECTION in X-AXIS -y = |x| (x, -y) For example: y = -1/10|x| 1/10 y = |x|

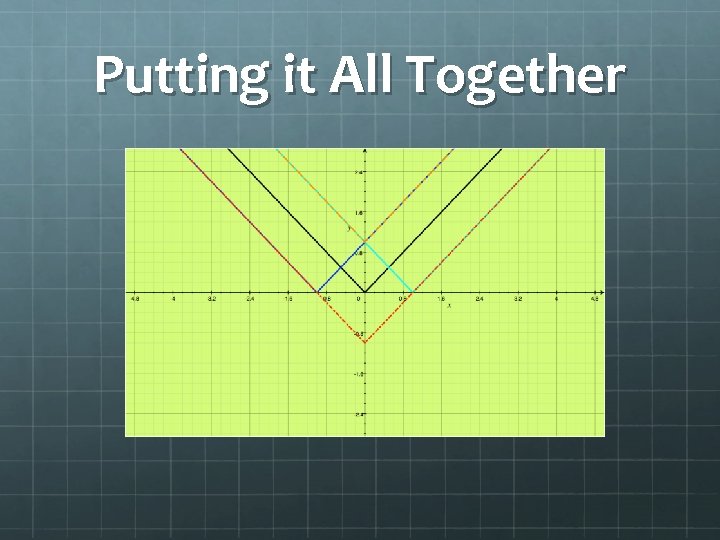
Putting it All Together

1) Graph the following absolute value functions and write its mapping notation: -1/2 (y+3) = |x+5| y-3 = |x+3| 1/4 y= |x-2|

2) Write the absolute value functions of the following mapping notation and graph its transformation: (x , y) (x+1, y) (x, y) (x, y-4) (x, y) (x-3, y + 3) (x, y) (-x, y+5)

Assignment You will draw a shape using different kinds of graphs – linear, quadratic, exponential, and absolute value functions. There should only be one point of origin. Make sure your graphs are clear and accurate. Be as creative as you can. Below your graph: A) State the domain and range of your different graphs. B) If it is either quadratic or absolute value functions, write its mapping notations. Deadline : December 26, 2012

Homework FOCUS QUESTIONS # 30 and 31 on page 186. CYU # 33, 34, 35, 36 and 37 on pages 187 -189.