4 3 Fundaments of Biomechanics 4 3 Biomechanics

4. 3 Fundaments of Biomechanics

4. 3 – Biomechanics • Biomechanics studies the forces caused by, and applied to, the human body and the effect they have on the body’smotion. • A deep understanding of biomechanics by an athlete or coach has two big benefits: • Improvement of technique • Reduction of injuries • Biomechanics is divided into 2 areas of study: KINEMATIC S KINETICS

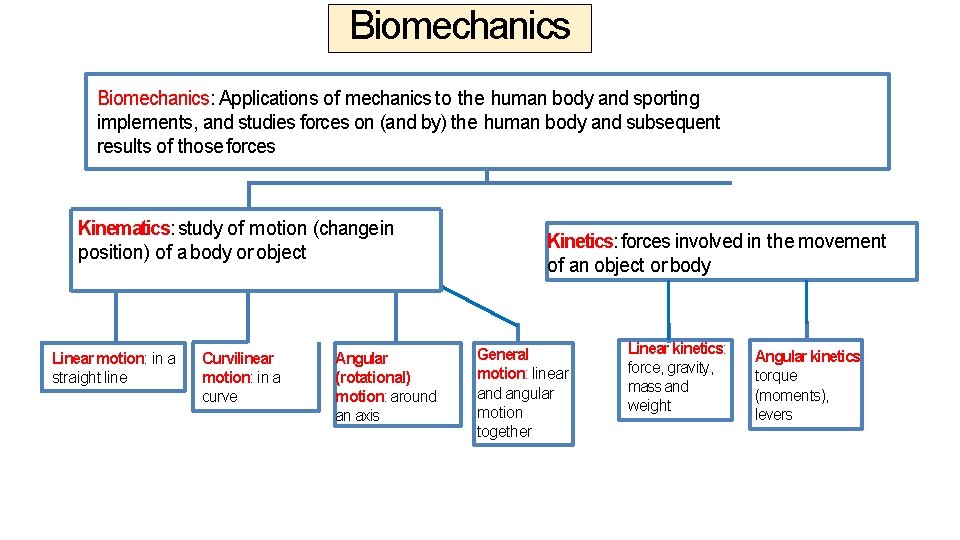
Biomechanics: Applications of mechanics to the human body and sporting implements, and studies forces on (and by) the human body and subsequent results of those forces Kinematics: study of motion (change in position) of a body or object Linear motion: in a straight line Curvilinear motion: in a curve Angular (rotational) motion: around an axis Kinetics: forces involved in the movement of an object or body General motion: linear and angular motion together Linear kinetics: force, gravity, mass and weight Angular kinetics: torque (moments), levers

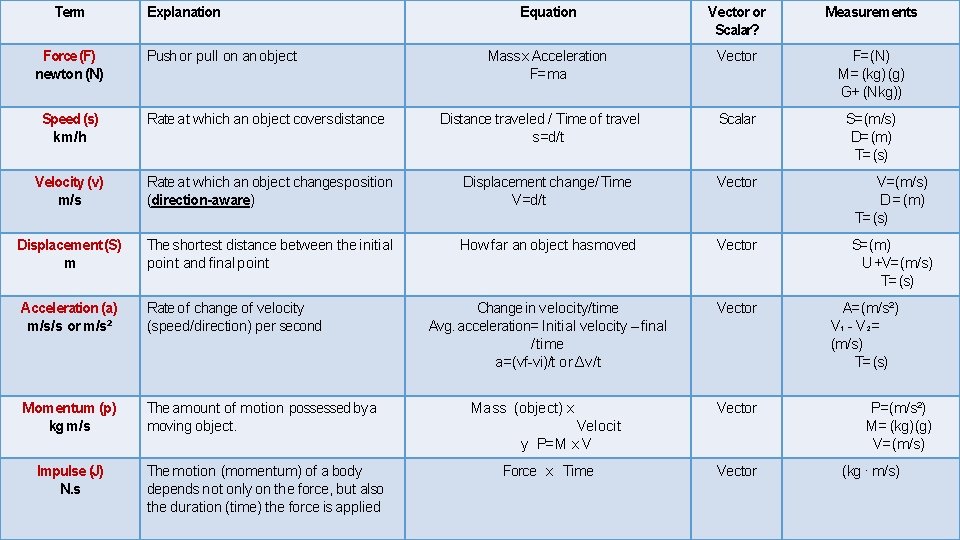
Term Force (F) newton (N) Explanation Push or pull on an object Equation Vector or Scalar? Measurements Mass x Acceleration F= ma Vector F= (N) M= (kg) (g) G+ (N kg)) Scalar S= (m/s) D= (m) T= (s) Speed (s) km/h Rate at which an object covers distance Distance traveled / Time of travel s=d/t Velocity (v) m/s Rate at which an object changes position (direction-aware) Displacement change/ Time V=d/t Vector V= (m/s) D = (m) T= (s) Displacement (S) m The shortest distance between the initial point and final point How far an object has moved Vector S= (m) U +V= (m/s) T= (s) Acceleration (a) m/s/s or m/s² Rate of change of velocity (speed/direction) per second Change in velocity/time Avg. acceleration= Initial velocity – final /time a=(vf-vi)/t or Δv/t Vector Momentum (p) kg m/s The amount of motion possessed by a moving object. Impulse (J) N. s The motion (momentum) of a body depends not only on the force, but also the duration (time) the force is applied Mass (object) x Vector Velocit y P= M x V Force x Time Vector A= (m/s²) V₁ - V₂= (m/s) T= (s) P= (m/s²) M= (kg) (g) V= (m/s) (kg · m/s)

Physics 101 Important Definitions FORCE F Mass x Acceleration SPEED s Distance / Time VELOCITY v Distance / Time DISPLACEMENT δ How far an object has moved ACCELERATION a Distance/Time MOMENTUM p Mass x Velocity IMPULSE J Force x Time

Kinematics • Deals with motion of bodies/object- change in position of a body or object • Answers four questions: How long? How far? How fast? How consistent? • Motion can be: • Linear= motion in a straight line with same direction and same speed (hockey puck pass) Circular motion about • Curvilinear= motion curve (shot-put in air) a point. i. e. The elbow being fixed when the • Angular= around an axis (gymnast around a high bar) forearm moves in a • When a body/part moves in a circle about a point (axis or rotation) • General= combination of linear and angular motion • Javelin, wheel chair, swimming, running half circle in a tennis serve.

Kinematics • Kinematics deals with both vectors and scalars • Important to understand the difference because it affects how measurements are combined. • Vectors measure both magnitude (size) and direction • Represented by arrows • Length of vector is proportional to magnitude of the variable • Scalars measures magnitude (size) • Has no particular direction associated with them • Ex: length of time it takes to run 100 m or speed posted on road sign (60 mph/hr. )

Kinetics • Deals with forces involved in the movement of an object/body and measured in newtons (N). • Force= Mass x Acceleration (vector)…why? • Forces that produce the movement and the resulting motion • Can be internal or external force: • Internal: forces generated by muscles pulling on bones (tendons) across joint surfaces. • External: forces acting without (gravity) or any body contact with the ground, environment, sport equipment, person, etc.

Vector vs. Scalar Vector Scalar • Displacement • Direction • Velocity • Acceleration • Momentum • Force • Impulse • Weight • Length • Mass • Area • Volume • Speed • Density • Pressure

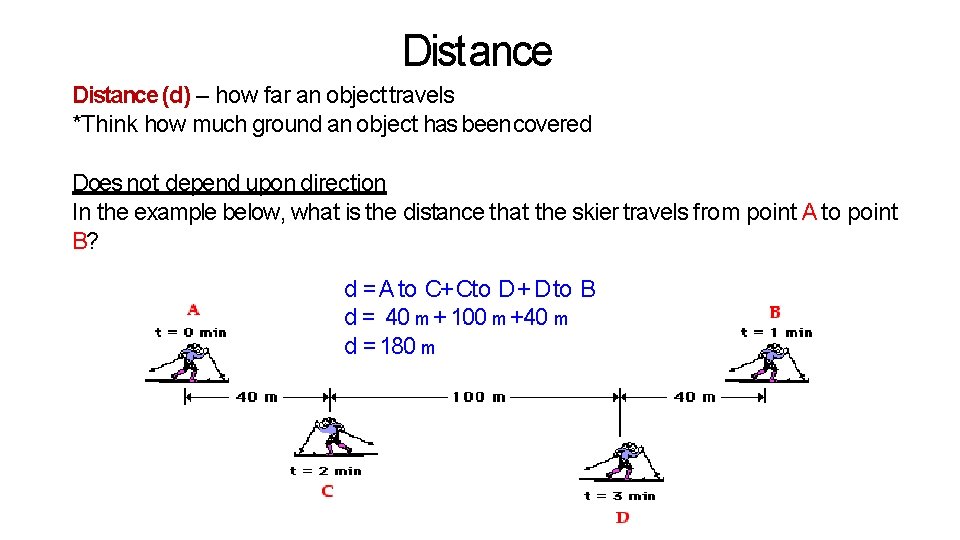
Distance (d) – how far an object travels *Think how much ground an object has been covered Does not depend upon direction In the example below, what is the distance that the skier travels from point A to point B? d = A to C+ Cto D + D to B d = 40 m + 100 m +40 m d = 180 m

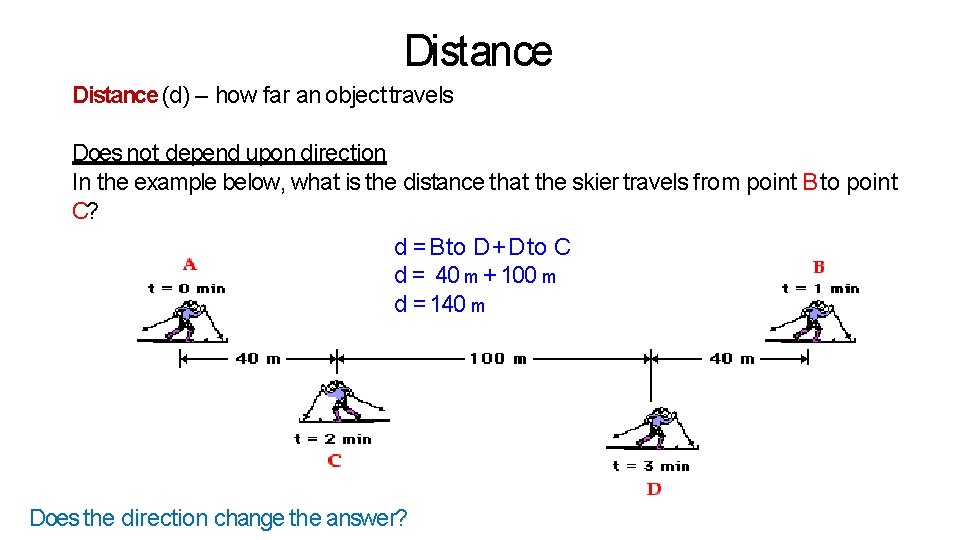
Distance (d) – how far an object travels Does not depend upon direction In the example below, what is the distance that the skier travels from point B to point C? d = Bto D + D to C d = 40 m + 100 m d = 140 m Does the direction change the answer?

Displacement (s) – the difference between an objects final position (Rf) and its initial position (Ri) ∆’s = change Displacement DOESdepend on direction *Think how far out of place an object is…if it’s a 5 k trail loop, displacement= 0 In order to define displacement, we need direction. Example of directions: • + and – • N, S, E, W • Angles

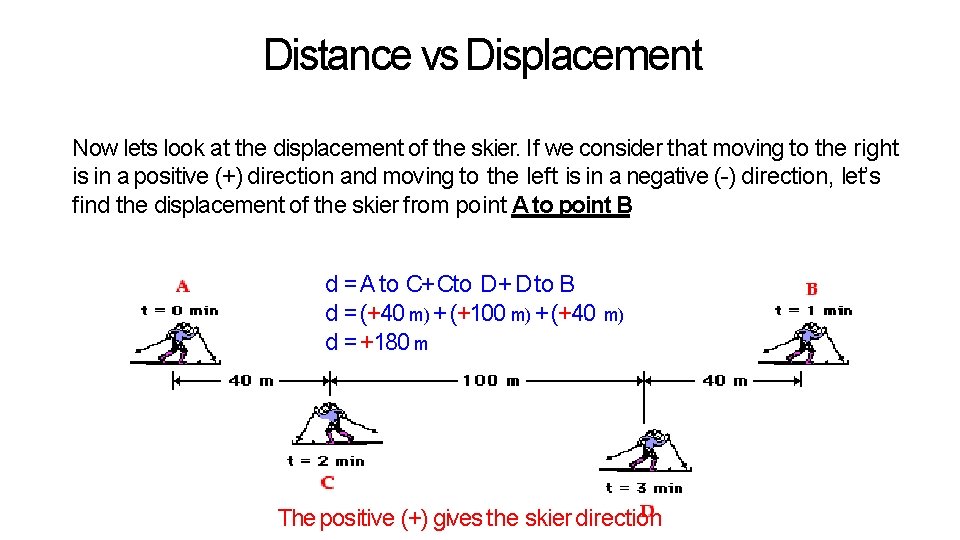
Distance vs Displacement Now lets look at the displacement of the skier. If we consider that moving to the right is in a positive (+) direction and moving to the left is in a negative (-) direction, let’s find the displacement of the skier from point A to point B d = A to C+ Cto D + D to B d = (+40 m) + (+100 m) + (+40 d = +180 m m) The positive (+) gives the skier direction

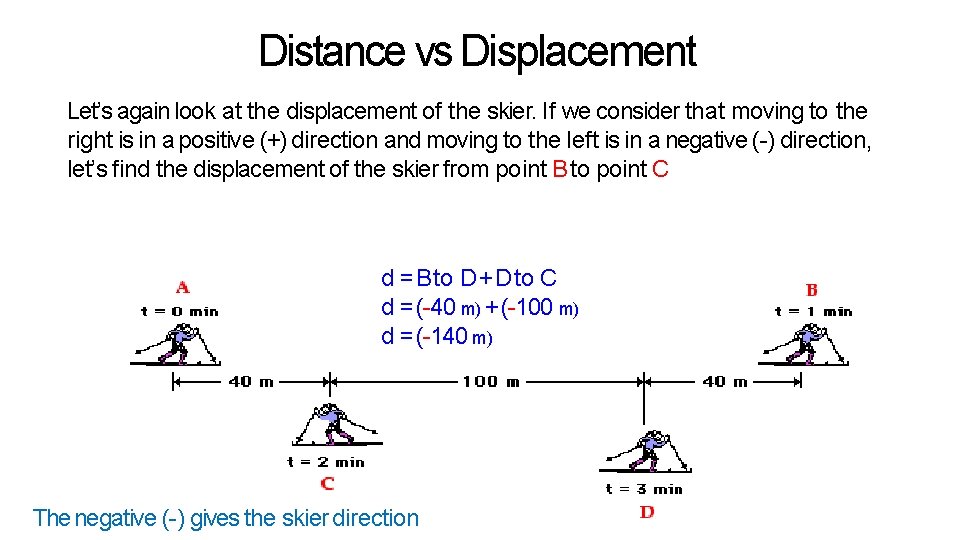
Distance vs Displacement Let’s again look at the displacement of the skier. If we consider that moving to the right is in a positive (+) direction and moving to the left is in a negative (-) direction, let’s find the displacement of the skier from point B to point C d = Bto D + D to C d = (-40 m) + (-100 m) d = (-140 m) The negative (-) gives the skier direction

Distance vs Displacement Find the displacement of the skier as they travel from point A to point B to point C and finally to point D. What is their final displacement? d = A to B d = Bto C d = Cto D +180 m -140 m +100 m 180 – 140 + 100 = +140

Distance vs Displacement An athlete runs around a 400 m track three times, then they stop. What is the distance traveled? 1200 m What is the displacement? 0 m

Displacement 1. Q: A car moved 80 km to the South. What is its displacement? A: 20 km South B: 50 km East C: 80 km South D: 160 km North 2. Q: A car moved 60 km East and 90 km West. What is the distance? A: 30 km B: 60 km C: 90 km D: 150 km 3. Q: A car moved 60 km East and 90 km West. What is the displacement? A: 30 km West B: 60 km West C: 30 km East D: 150 km

4. Q: Average velocity can be calculated by dividing displacement over what? A: time B: distance C: mass D: density 5. Q: What is the average velocity of a car that moved 60 km in 3 hours? A: 10 km/h B: 20 km/h C: 30 km/h D: 60 km/h 6. Q: What is the average velocity of a car that moved 40 km East and 80 km West in 2 hours? A: 5 km/h B: 10 km/h C: 15 km/h D: 20 km/h 7. Q: How far will a car travel in 25 min at 12 m/s? A : 10 km B: 14 km C: 18 km D: 24 km

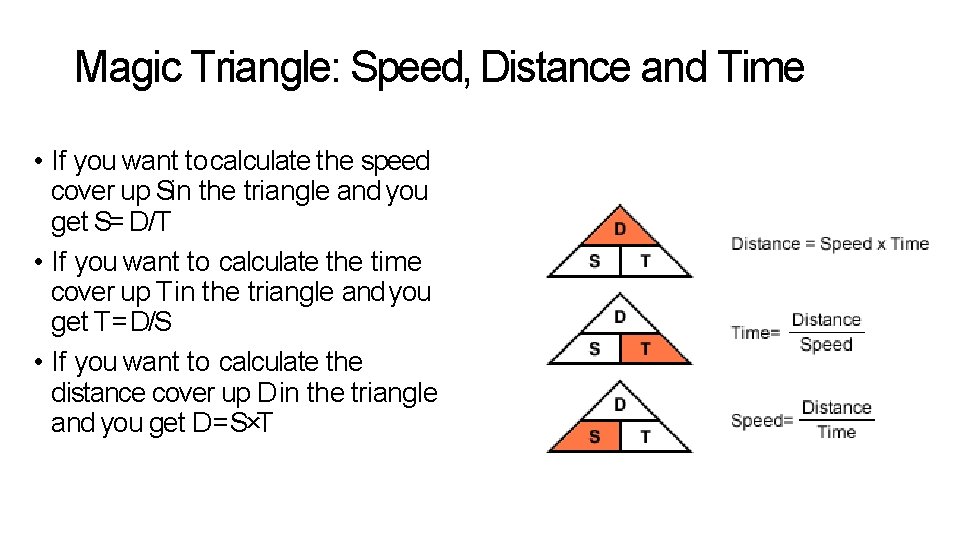
Magic Triangle: Speed, Distance and Time • If you want to calculate the speed cover up Sin the triangle and you get S= D/T • If you want to calculate the time cover up Tin the triangle and you get T= D/S • If you want to calculate the distance cover up D in the triangle and you get D =S×T

Speed vs Velocity Speed is simply how fast you are travelling -based on distance Speed = Distance travelled Time taken Yohan Blake is travelling at a speed of 10 m/s Meters Secon d Velocity is speed in a given direction -based on displacement Velocity = Displacement Time taken Meters Second Yohan Blake is travelling at a speed of 10 m/s East Similar= have same magnitude (size)…but speed does not have direction, whereas velocity has direction AND speed

Practice: Usain Bolt ran 100 m in 9. 58 seconds, what was his average speed? 10. 43 m/s

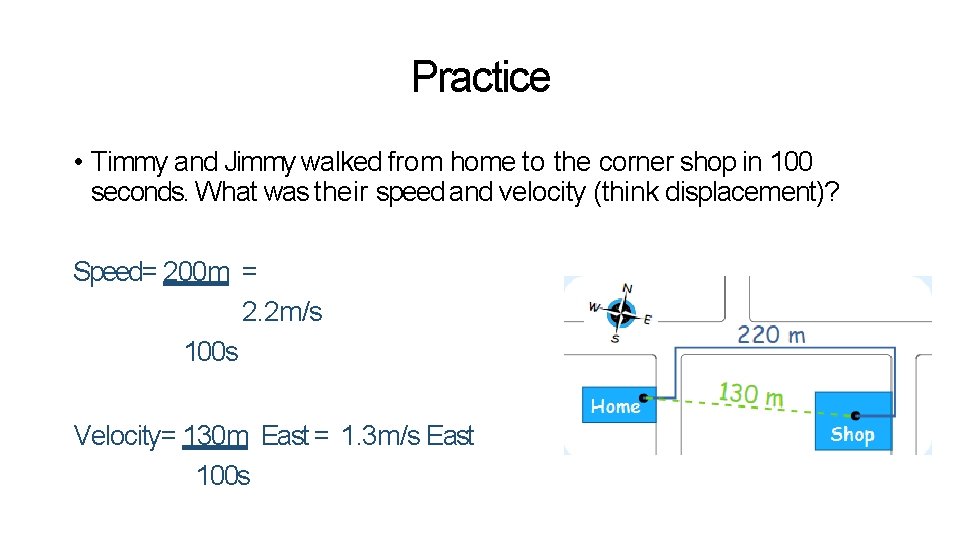
Practice • Timmy and Jimmy walked from home to the corner shop in 100 seconds. What was their speed and velocity (think displacement)? Speed= 200 m = 2. 2 m/s 100 s Velocity= 130 m East = 1. 3 m/s East 100 s

Practice Alex Morgan kicks a ball 6. 5 meters. How much time is needed for the ball to travel this distance if its velocity is 22 meters per second, south? t= d/s = 6. 5 m / 22 ms-1 = 0. 3 s

Practice Andy Murray serves a tennis ball to Rafael Nadal. It travels 9. 5 meters south in 2. 1 seconds. a. What is the velocity of the tennis ball? v= d/t = 9. 5 m/2. 1 s = 4. 5 ms-1 South If the tennis ball travels at constant speed, what is its velocity when Nadal returns Murray’s serve? 4. 5 ms-1 north

Practice Acceleration = Change in velocity (final speed-starting speed) Time (taken) A skater goes from a standstill to a speed of 6. 7 m/s in 12 seconds. What is the acceleration of the skater? 6. 7 m/s = 0. 56 m/s 2 12 s A cyclist’s speed changes from 2 m/s to 7 m/s in 4. 2 s. What is their acceleration? 5 m/s = 1. 19 m/s 2 4. 2 s

More practice During a 1600 m race, a runner starts their kick to the finish at the 1400 m mark to the finish at 1600 m, it takes them 28 seconds to cover that distance. What is their average speed? 200 m = 7. 14 m/s 28 s Tough one! 6. A cyclist is traveling at an average speed of 12 m/s. After 15 minutes how far will they have traveled? 15 min x 60 s = 900 s 12 m/s x 900 x = 10, 800 m or 10. 8 km

Momentum • A vector describing a “quantity of motion” and is the product of mass and velocity • More momentum an object/body has, the harder to stop. • Requires greater amount of force or longer amount of time (or both) to stop object. • Object with momentum can be stopped if force applied against it for a given amount of time. ***An athlete can increase their momentum by either increasing their mass or velocity What role does “padding” play in sports? NFL= defensive player applies a force for a given amount of time to stop the momentum of the offensive player with the ball.

Impulse • Important when studying collisions • The quantity of force…. or “force felt during a collision multiplied by the duration of the collision” • Impulse= (force) x (time) • Change in momentum • When a force is applied to an object, the resulting motion of the body is dependent on the duration of the force applied, as well as the motion of the body.

Why are the following variable important in maximizing impulse? • Speed • Strength • Flexibility

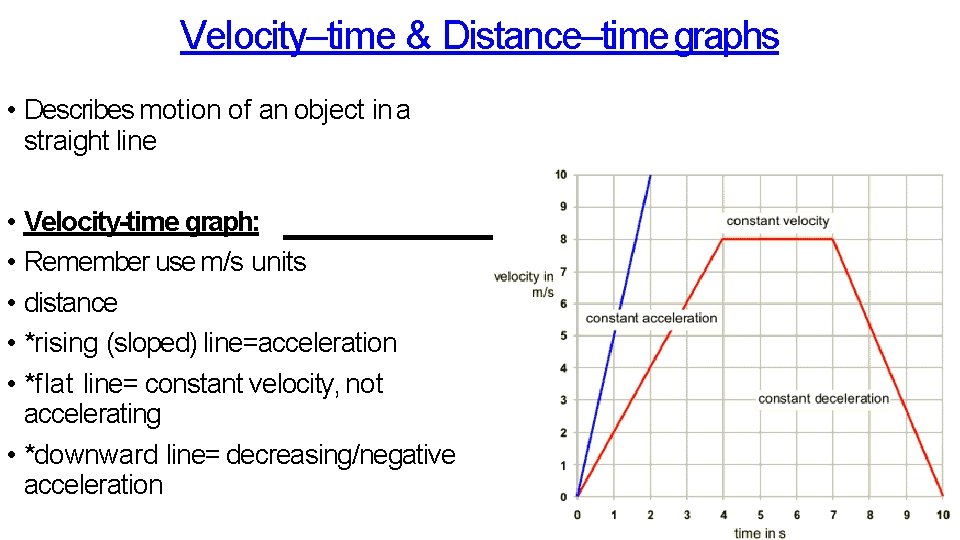
Velocity–time & Distance–time graphs • Describes motion of an object in a straight line • Velocity-time graph: • Remember use m/s units • distance • *rising (sloped) line=acceleration • *flat line= constant velocity, not accelerating • *downward line= decreasing/negative acceleration

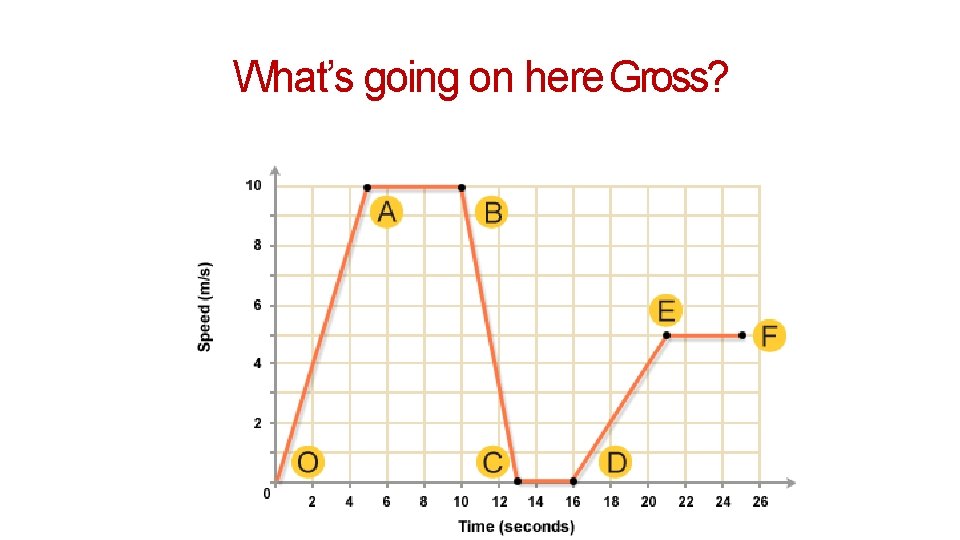
What’s going on here Gross?

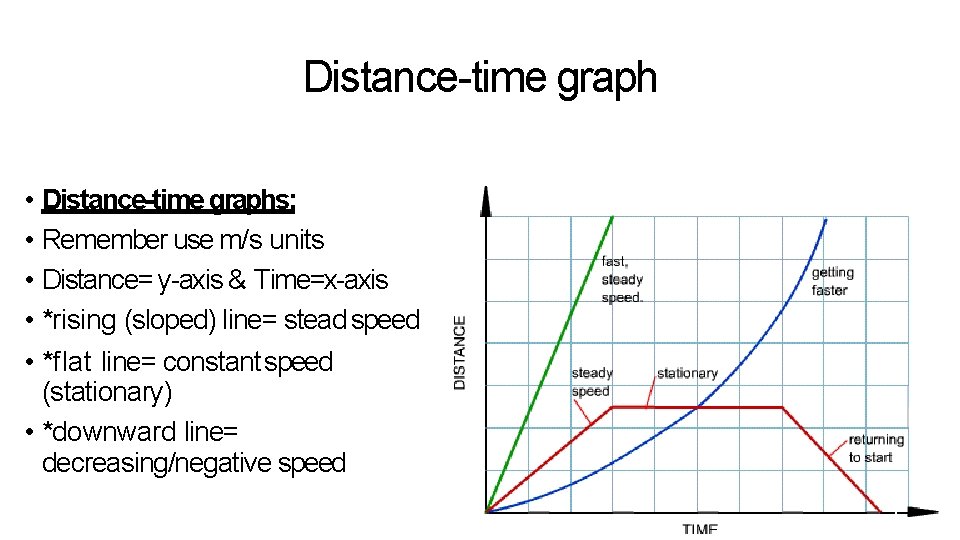
Distance-time graph • Distance-time graphs: • Remember use m/s units • Distance= y-axis & Time=x-axis • *rising (sloped) line= stead speed • *flat line= constant speed (stationary) • *downward line= decreasing/negative speed

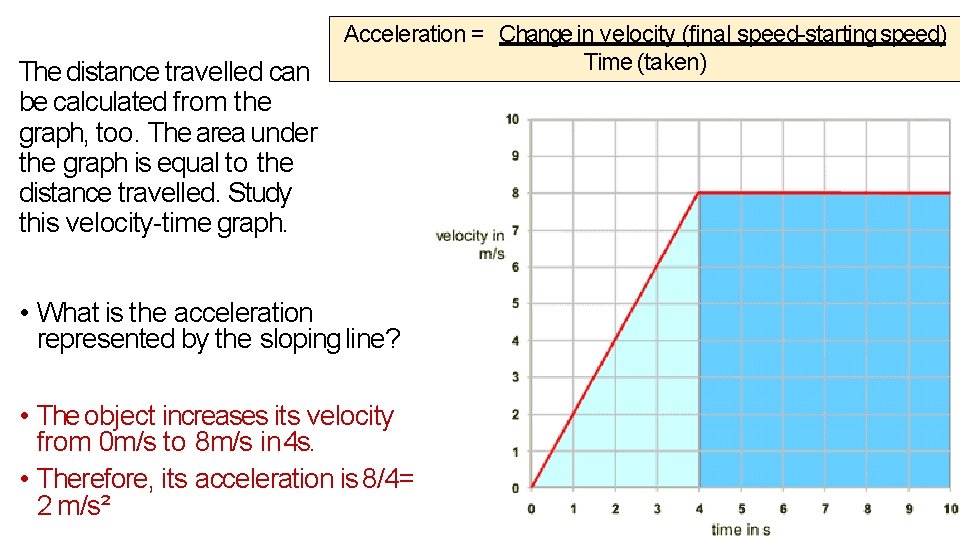
The distance travelled can be calculated from the graph, too. The area under the graph is equal to the distance travelled. Study this velocity-time graph. Acceleration = Change in velocity (final speed-starting speed) Time (taken) • What is the acceleration represented by the sloping line? • The object increases its velocity from 0 m/s to 8 m/s in 4 s. • Therefore, its acceleration is 8/4= 2 m/s²

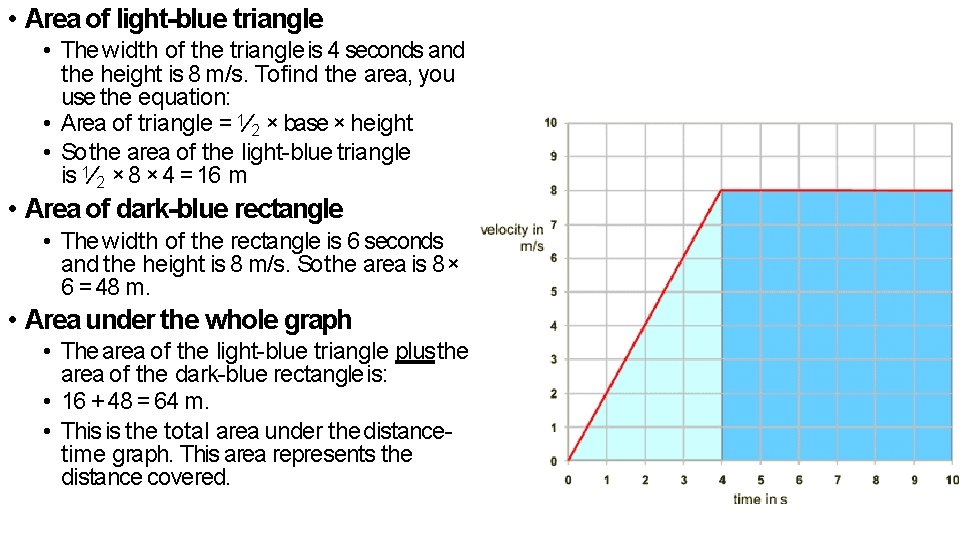
• Area of light-blue triangle • The width of the triangle is 4 seconds and the height is 8 m/s. Tofind the area, you use the equation: • Area of triangle = 1 ⁄ 2 × base × height • So the area of the light-blue triangle is 1 ⁄ 2 × 8 × 4 = 16 m • Area of dark-blue rectangle • The width of the rectangle is 6 seconds and the height is 8 m/s. So the area is 8 × 6 = 48 m. • Area under the whole graph • The area of the light-blue triangle plus the area of the dark-blue rectangle is: • 16 + 48 = 64 m. • This is the total area under the distancetime graph. This area represents the distance covered.

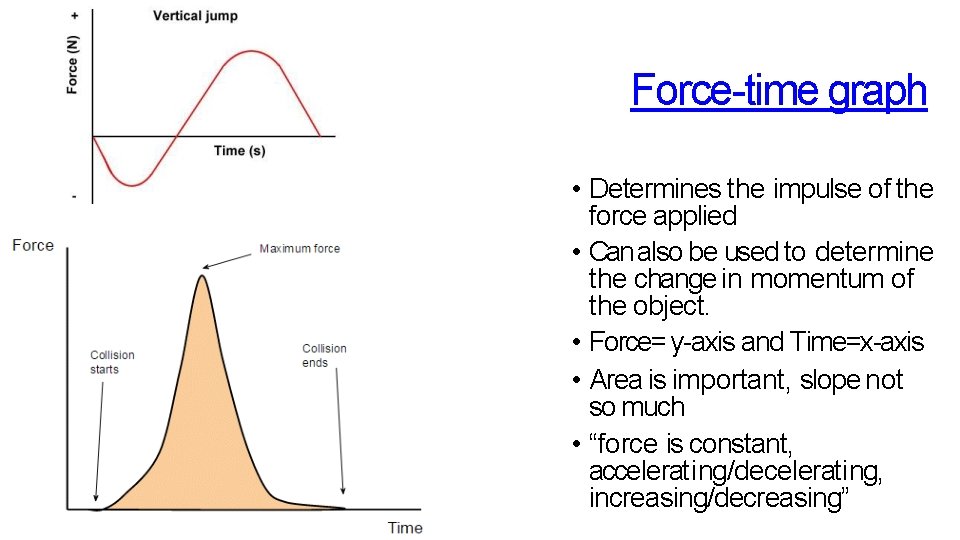
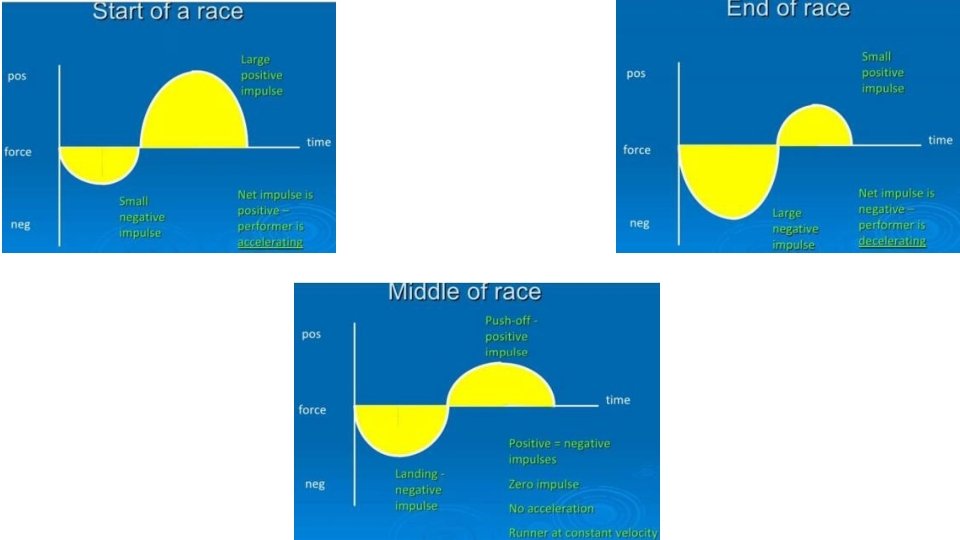
Force-time graph • Determines the impulse of the force applied • Can also be used to determine the change in momentum of the object. • Force= y-axis and Time=x-axis • Area is important, slope not so much • “force is constant, accelerating/decelerating, increasing/decreasing”

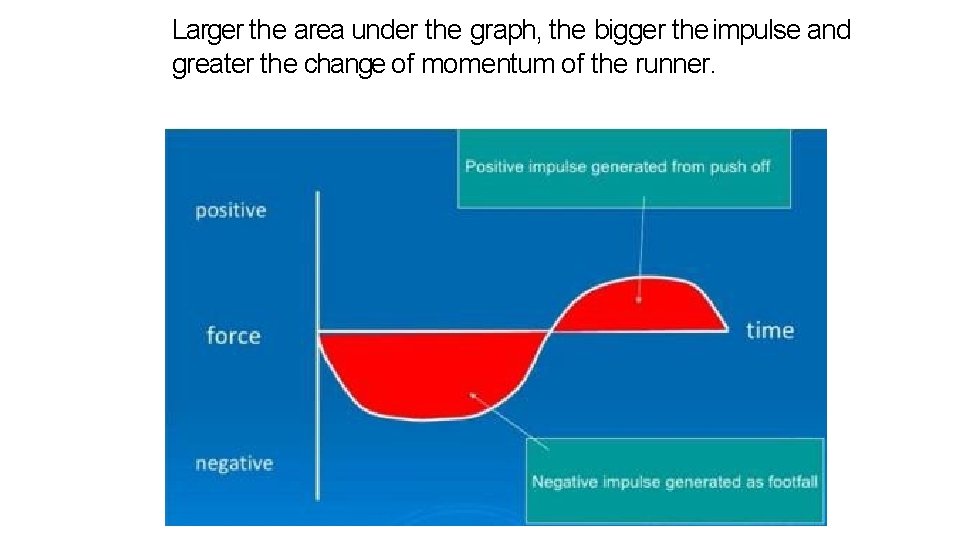
Larger the area under the graph, the bigger the impulse and greater the change of momentum of the runner.

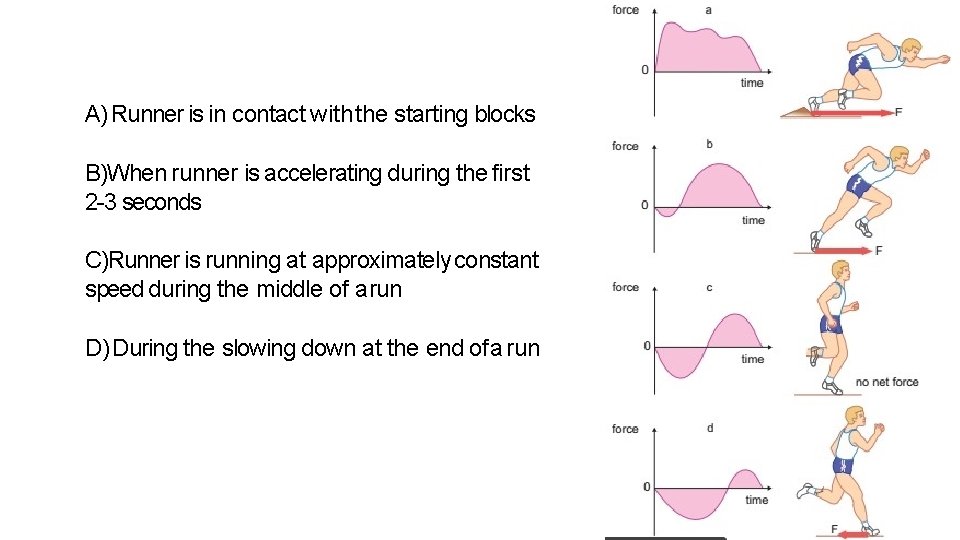
A) Runner is in contact with the starting blocks B)When runner is accelerating during the first 2 -3 seconds C)Runner is running at approximately constant speed during the middle of arun D) During the slowing down at the end of a run

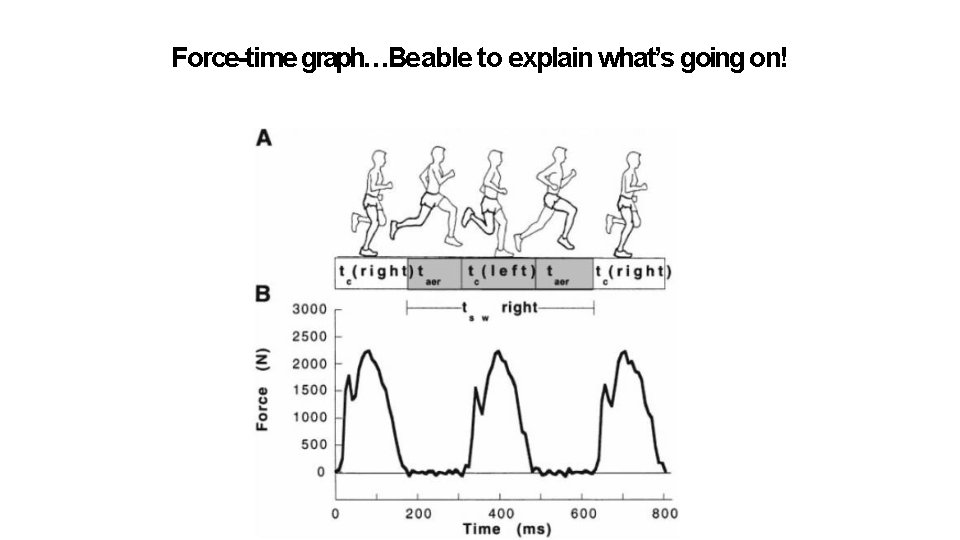
Force-time graph…Be able to explain what’s going on!

Force Triangle: Mass, Density and Volume • Mass = Density x Volume • Density = Mass ÷ Volume • Volume = Mass ÷ Density

Center of Mass and Center Of Gravity • The center of mass is the point in which the mass of a body is evenly distributed. • The center of gravity is the point at which the force of gravity is acting. • In the human body, the center of mass will be in a different place for individuals with different body types, ages, and gender. • A person can change his/her center of mass by moving body segments (limbs) around.

3 Reasons Why It’s Important to Know the Center of Mass 1. Determines the stability of static positions (balance). 2. It represents the axis for all free airborne rotations of the body (summersaulting). 3. It is the reference point when considering whole body translation (long jump).

Base of Support • Base of support is the location on a body or object where most of the weight is supported. • The larger the area the BOScovers, the more stable an object will be.

Line of gravity • The line of gravity is an imaginary vertical line passing through the center of gravity down to a point in the base of support. • If the line of gravity falls within the object’s base of support (i. e. its contact with the ground), the object is relatively stable. • If the line of gravity falls outside the object’s base of support (i. e. its contact with the ground), the object is relatively unstable.

LOG, BOSandmovement The line of gravity (LOG) must go outside the base of support to initiate or continue movement. The direction that the line of gravity relative to the BOSwill be the direction of the resulting movement. The further away the LOGis from the BOS, the greater the tendency the body has to move in that direction. E. g. Starting blocks

High jump- Scissor Kick vs. Fosbury Flop • The athlete bends their body like a banana around the bar and their center of mass is below and outside the body (may be below bar). • The jumper using the Fosbury technique will not have to raise their CM as high as an athlete performing the Scissor kick when clearing an equal height. • A jumper using the Fosbury technique will be able to clear a higher bar compared to using the Scissor kick. Scissor Kick • The upper body is upright and the legs are horizontal to the body- this puts the CM above the legs, hips and bar.

Now think of a examples in sport where the center of mass… • Changes and benefits your performance • You change in order to benefit your performance • Changes and negatively impacts your performance • Can potentially be outside of your body

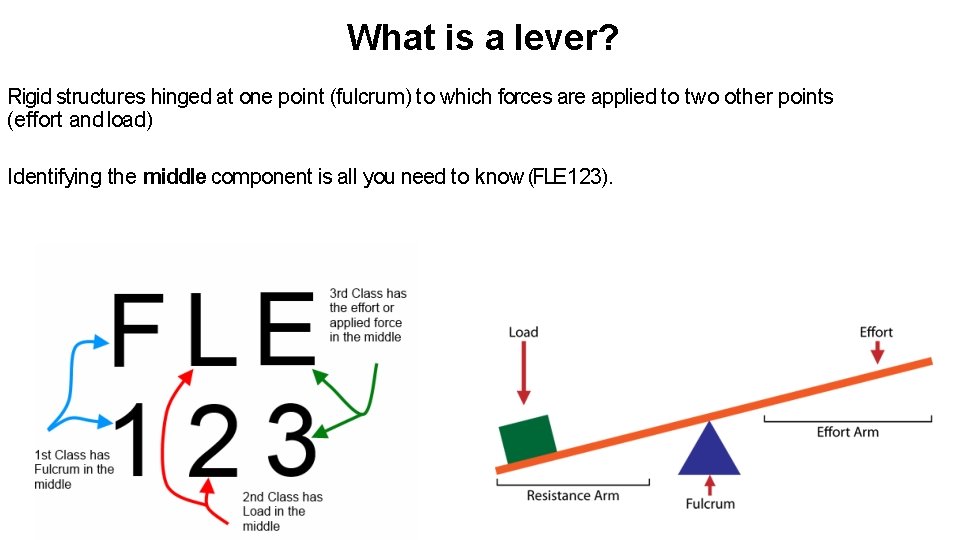
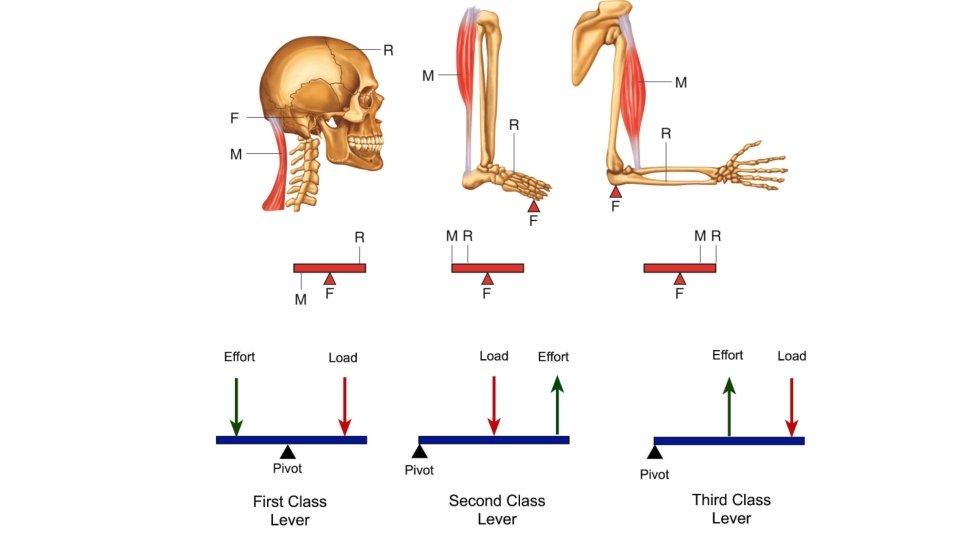
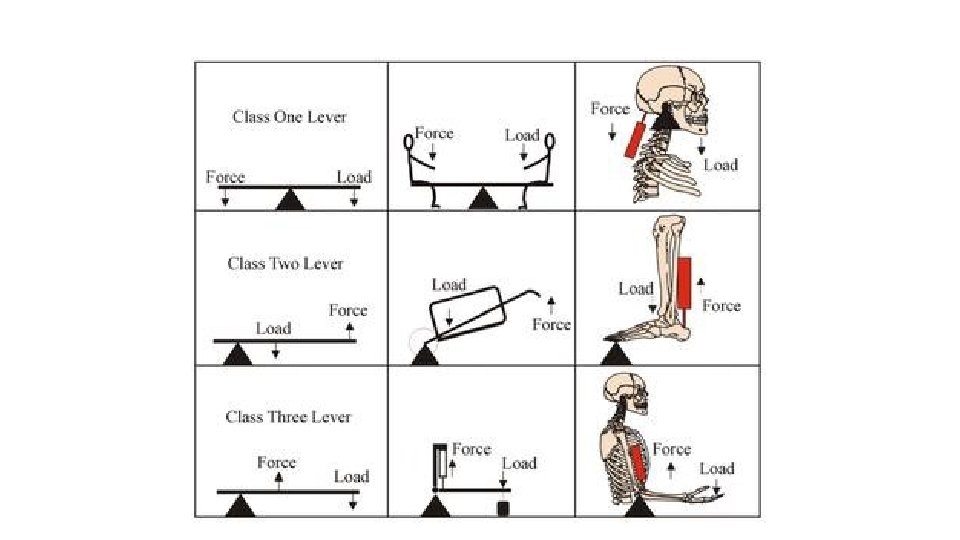
What is a lever? Rigid structures hinged at one point (fulcrum) to which forces are applied to two other points (effort and load) Identifying the middle component is all you need to know (FLE 123).

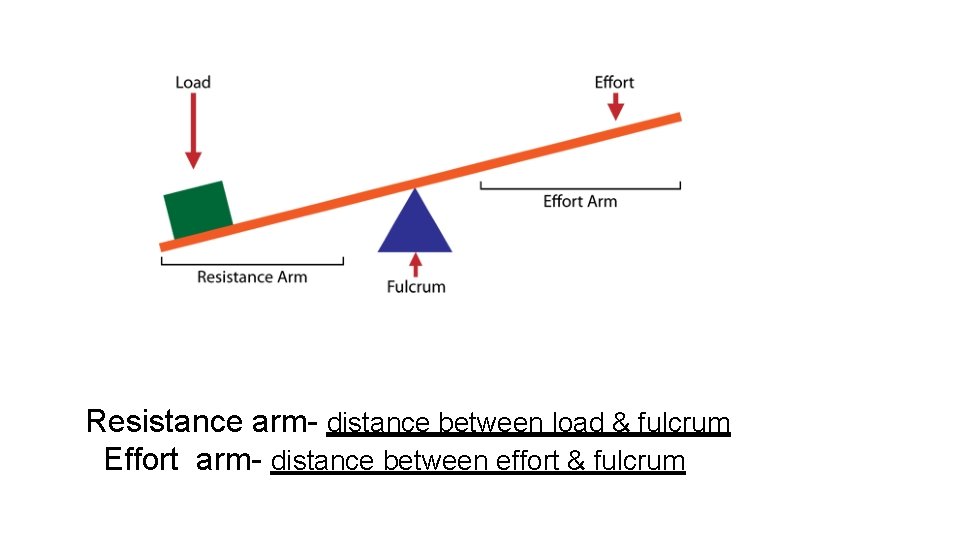
Resistance arm- distance between load & fulcrum Effort arm- distance between effort & fulcrum

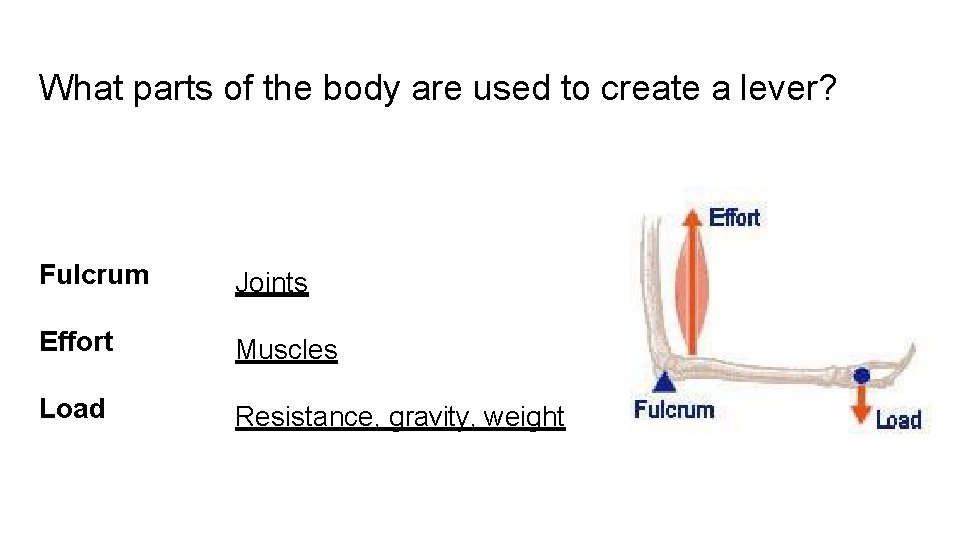
What parts of the body are used to create a lever? Fulcrum Joints Effort Muscles Load Resistance, gravity, weight

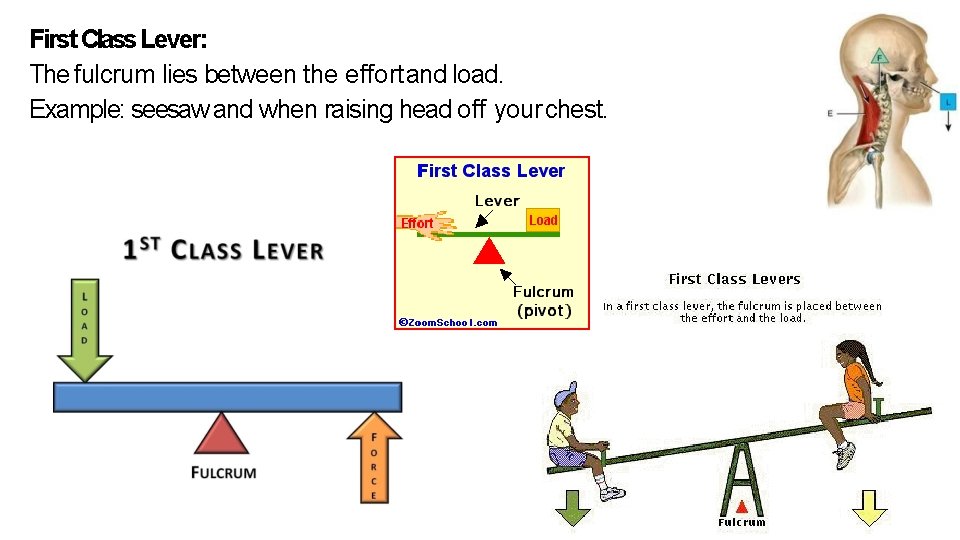
First Class Lever: The fulcrum lies between the effort and load. Example: seesaw and when raising head off your chest.

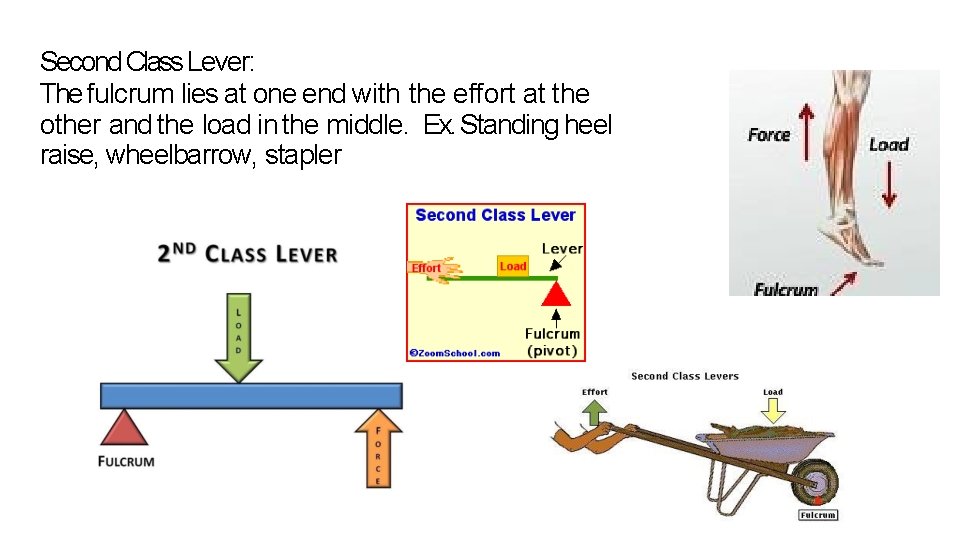
Second Class Lever: The fulcrum lies at one end with the effort at the other and the load in the middle. Ex. Standing heel raise, wheelbarrow, stapler

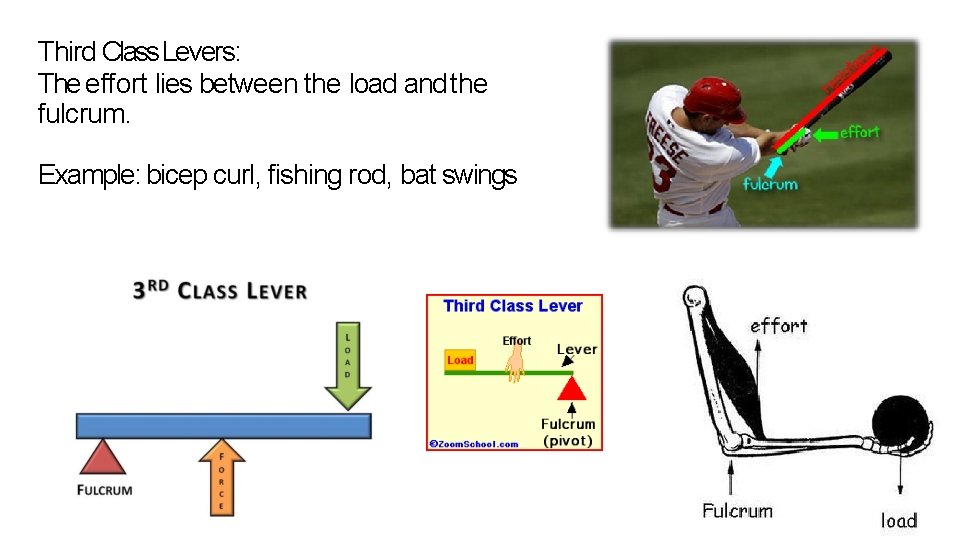
Third Class Levers: The effort lies between the load and the fulcrum. Example: bicep curl, fishing rod, bat swings

Long levers result in greater force at the end of a limb. This in beneficial for throwing or striking an object. Short lever can be moved with less force and at a greater speed. This is beneficial for moving body parts quickly and applying strength for pushing, pulling and lifting. How can the length of a limb change the how a lever functions?

How can a 5’ 10” pitcher be such a powerful pitcher? An excessively large stride increases the speed the arm can move as a 3 rd class lever. The normal stride length for a pitcher is 77% to 87% of his height. Lincecum's stride is 129%, some 7 1/2 feet

Load Effort Fulcrum

Newton’s 1 st Law Inertia A body/object in motion tends to keep moving until acted upon by outside forces.

Newton’s first law of motion (inertia) • “An object will remain at rest or continue with constant velocity unless acted on by an unbalanced force. ”

Newton’s 2 nd Law Force F= m x a

Newton’s second law of motion (acceleration) • “The acceleration is proportional to, and in the same direction as, the unbalanced force applied to it. ” • Force is equal to mass multiplied by acceleration (F=ma) • Relates to change in motion Determine the accelerations that result when a 12 -N net force is applied to a 3 -kg shot putt and then to a 6 -kg shot putt. A 3 -kg object experiences an acceleration of 4 m/s/s. A 6 -kg object experiences an acceleration of 2 m/s/s.

Newton’s 3 rd Law Reaction “For every action, there’s a reaction”

Newton’s second law (F=ma) • Suppose that a running back is has a total of 1000 N of force acting on them, causing them to accelerate at a rate of 5 m/s 2. Determine the mass of the player. • force (N)= Mass (kg) x acceleration (m/s) • mass= force/acceleration • Mass=1000/5 • Mass= 200 kg

Newton’s third law of motion (reaction) • “When one body/object applies a force to another, the second body/object will apply a force equal in size but opposite in direction to the first body/object. ” • “For every action there’s an equal and opposite reaction”

Momentum conservation principle • For a collision occurring between person 1 and person 2 in an isolated system, the total momentum of the two people before the collision is equal to the total momentum of the two people after the collision. • That is…the momentum lost by person 1 is equal to the momentum gained by person 2…conservation occurs (momentum remains same or “constant”) • “Conserved” means “constant” or “not changing”

Angular momentum • Angular momentum (L): the quantity of rotation about an axis. • Product of moment of inertia multiplied by angular velocity about chosen axis. (L =I w) • Is constant and conserved when the net torque is zero • Vector quantity: magnitude and direction • Three factors: mass, distribution of mass with respect to the axis of rotation and angular velocity of the body. Generated by Torque: twisting force that causes rotation

Moment of Inertia • How difficult it is for a body to rotate about an axis. • Measured in Kgx m 2 • Depends on the mass of the object, but also the mass distribution around the axis. • More mass further away from the axis gives a greater moment of inertia and it will more difficult to rotate.

Conservation of Angular Momentum • During human airborne sports (gymnastics, diving, long/high jump), gravity is the major force acting on the body in motion. • The axis of rotation when a body is flying through the air passes through the center of gravity, therefore the force of gravity does not create torque as it goes through the axis of rotation (because the distance of the force from the axis of rotation is zero). • This means that there is no rotational effect of the force of gravity while the body is translating though space. So the angular momentum stays the same (is conserved) during flight. • Angular momentum is equal to the moment of inertia multiplied by the angular velocity. So when a gymnast “tucks” during a somersault, she will rotate faster because the moment of inertia will be reduced, thus speeding up angular velocity.

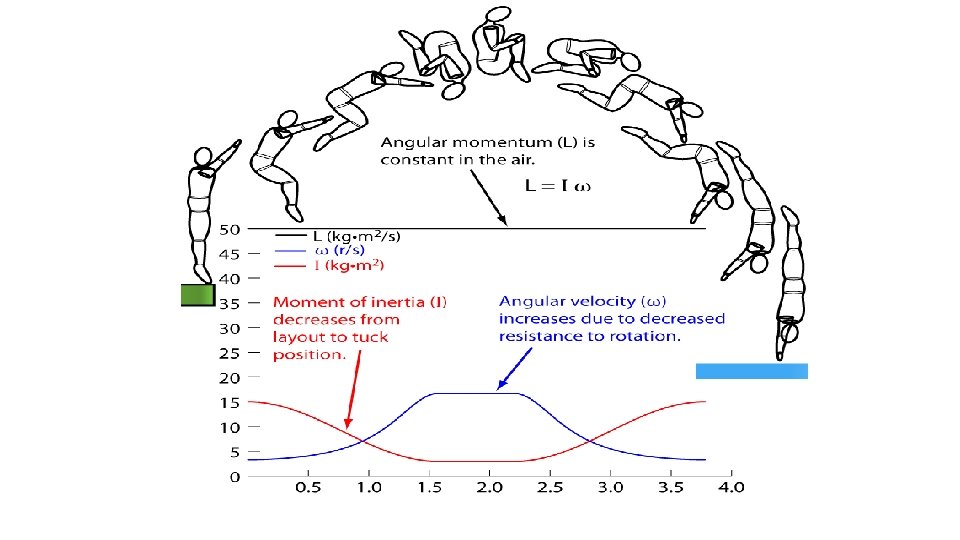
Figure Skating • In figure skating, the movement of the arms can reduce the skater’s moment of inertia. Drawing the arms inward towards the body, will reduce the distance between the axis of rotation, and reduce the moment of inertia as more mass closer to the axis (the body) results in a smaller moment of inertia and makes it easier to rotate. • Because angular momentum is conserved, the angular velocity will increase to compensate.

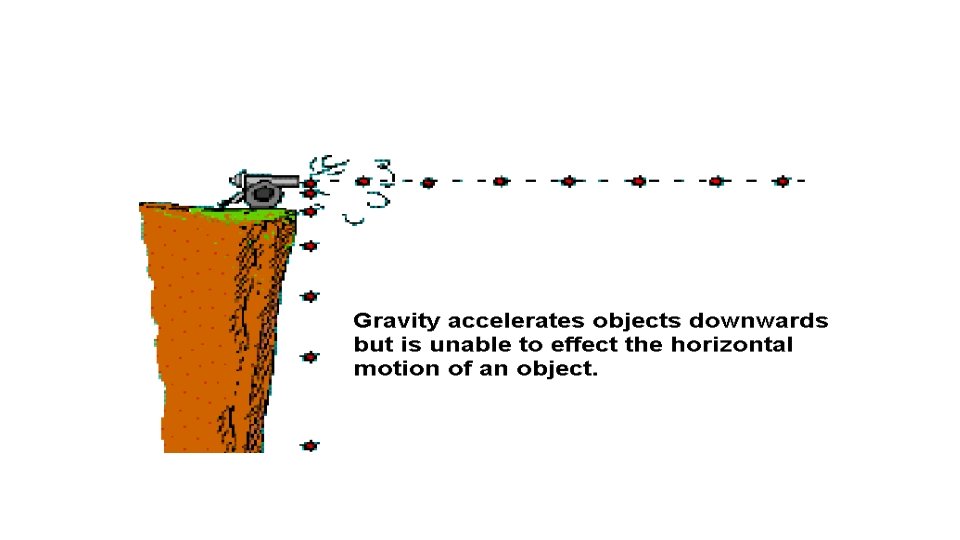
Projectiles in motion at take-off or release • Projectile: an object or body in free fall that’s subject to only the forces of gravity and air resistance. • Newton’s 1 st law states that things that are in motion keep moving without the need for an external force. • Therefore, once a force has been removed the object can no longer be altered. • This means that the path of the object is determined at the moment it leave the hand, floor, bat, etc.

Projectile motion refers to the motion of an object that is thrown, or projected into the air at an angle. The motion of a projectile is determined only by the object’s initial velocity and gravity.

Projectile motion is a combination of horizontal motion and vertical motion. The horizontal motion of a projectile is constant because no gravitational force acts horizontally The vertical motion of a projectile is nothing more than free fall with a constant downward acceleration due to gravity.

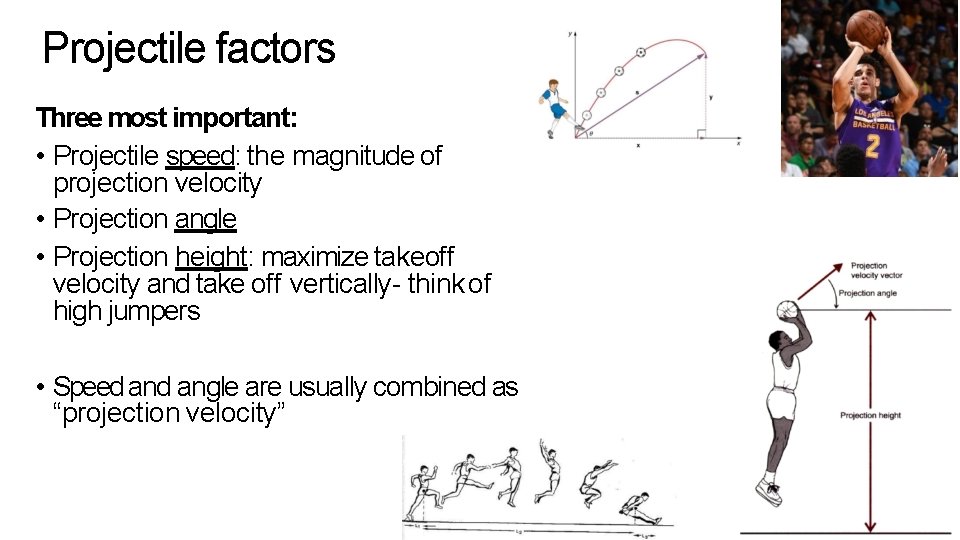
Projectile factors Three most important: • Projectile speed: the magnitude of projection velocity • Projection angle • Projection height: maximize takeoff velocity and take off vertically- think of high jumpers • Speed angle are usually combined as “projection velocity”

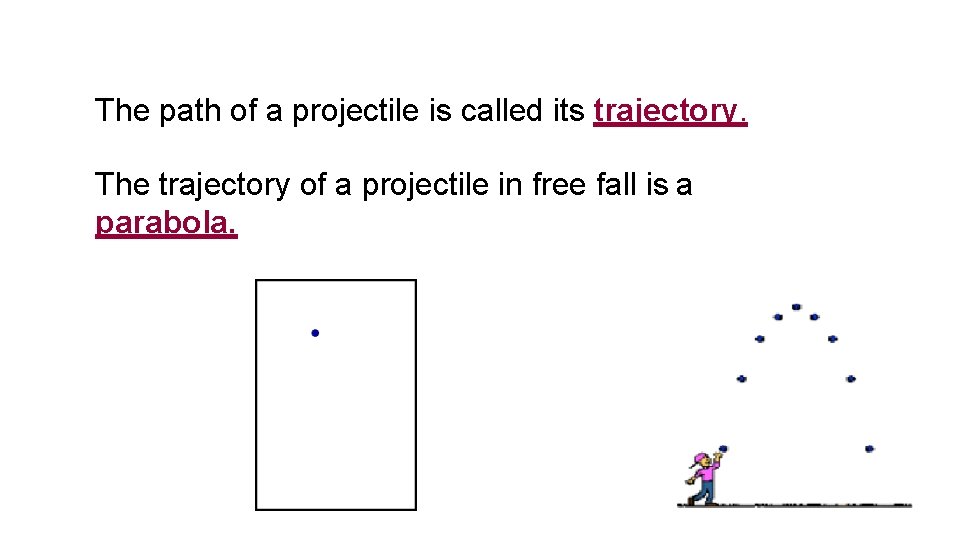
The path of a projectile is called its trajectory. The trajectory of a projectile in free fall is a parabola.

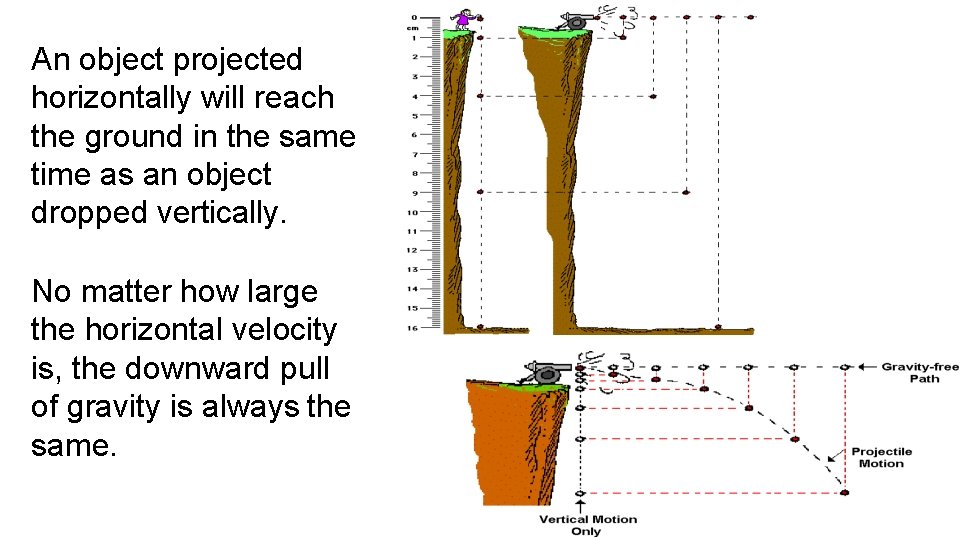
An object projected horizontally will reach the ground in the same time as an object dropped vertically. No matter how large the horizontal velocity is, the downward pull of gravity is always the same.

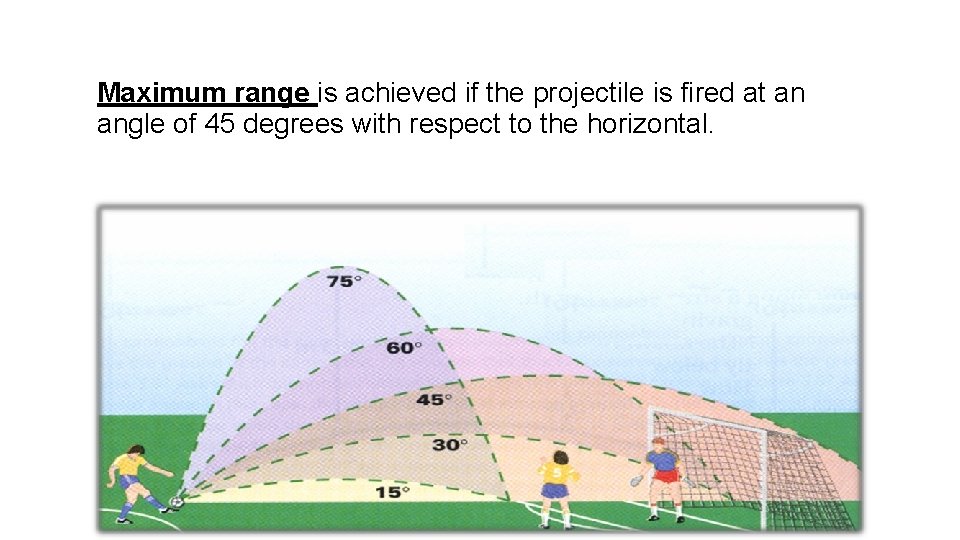
Maximum range is achieved if the projectile is fired at an angle of 45 degrees with respect to the horizontal.

Summary of Projectile Motion • In the throwing and jumping events, the optimum projection angle is usually considerably less than 45° because the speed an athlete can produce decreases as the projection angle is raised. • The optimum projection angle is different for every athlete. • Most athletes find their optimum projection angle relatively quickly through trial-and-error, and achieving a high projection speed is much more important than throwing or jumping at the optimum angle.

Fluid Dynamics • All athletic events take place in a fluid environment (water, air or both). A fluid is a substance that flows (liquid or gas). When we move, we causeair to flow around us. And since air resists motion, it slows us down. • The motion of the body/object is pushing apart molecules of the fluid, which the forces between molecules put a resistance to this, which applies force!

Fluid Forces • Two major forces in fluid dynamics: drag and lift force Drag force • Drag force and lift forces are perpendicular to each other, produce different effects and are affectedby different factors. • Flow velocity: the motion of the fluid flowing past an object or the motion of the object through the fluid. • What are fluid forces acting in the air called. . . ? • Aerodynamics! Lift force

FLUID DYNAMICS Drag: refers to forces acting opposite to the relative motion of any object moving with respect to a surrounding fluid. Think cycling- the faster one cycles, the greater the resistance. Thus, flexing at the hips and waist we present less surface area to the air…less resistance!

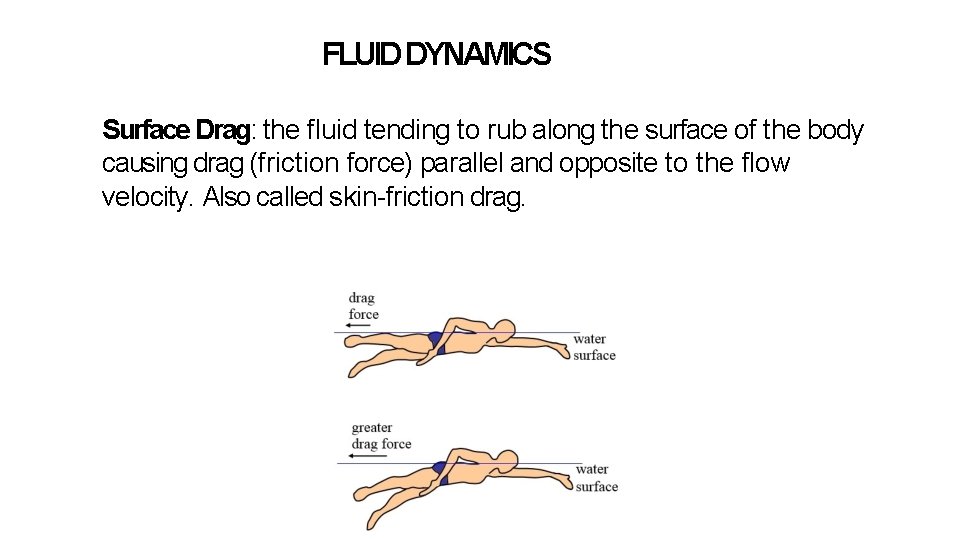
FLUID DYNAMICS Surface Drag: the fluid tending to rub along the surface of the body causing drag (friction force) parallel and opposite to the flow velocity. Also called skin-friction drag.

Surface Drag When swimming, the water must move around your body and limbs. A thin layer of water next to the body actually sticks to it, and moves with it causing up to 30% resistance. The overall effect of this is a considerable drag on the forward progress of the swimmer.

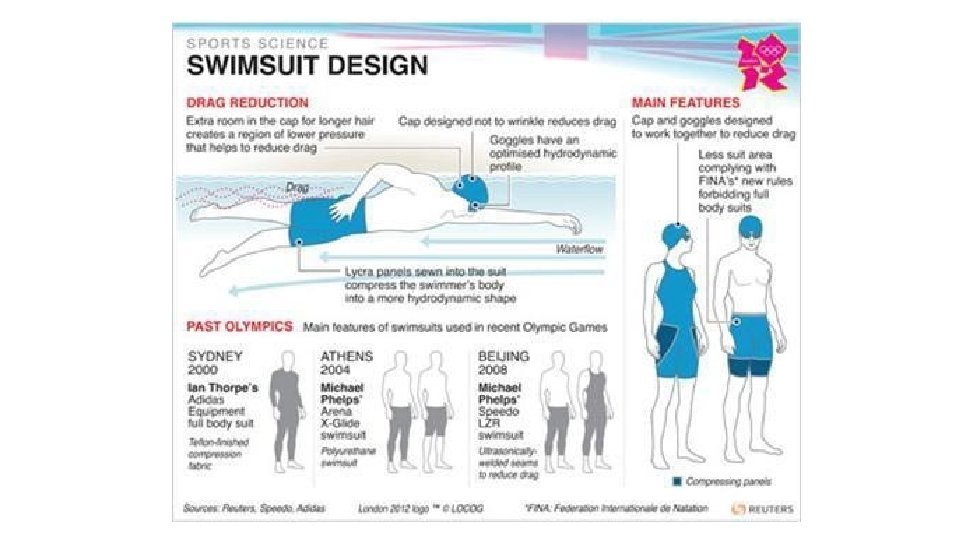
Form Drag • Form Drag: caused by the shape of the body or object and air turbulence produced by its shape as it moves through the air. • Common in skiing, cycling, running and all projectile events.

The Bernoulli Principle • Bernoulli's Principle is a physics principle that states the faster a gas or fluid is flowing, the lower its air pressure. The high pressure beneath the wing pushes up to cause lift. • The principle states that the total energy of a moving fluid remains constant at all times. • Therefore fluid pressure is inversely proportional to fluid velocity.

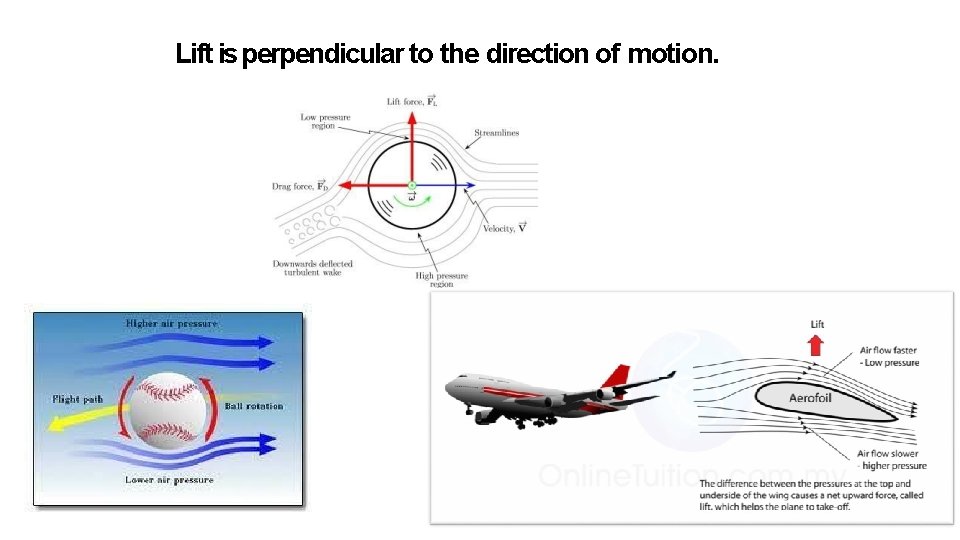
Lift is perpendicular to the direction of motion.

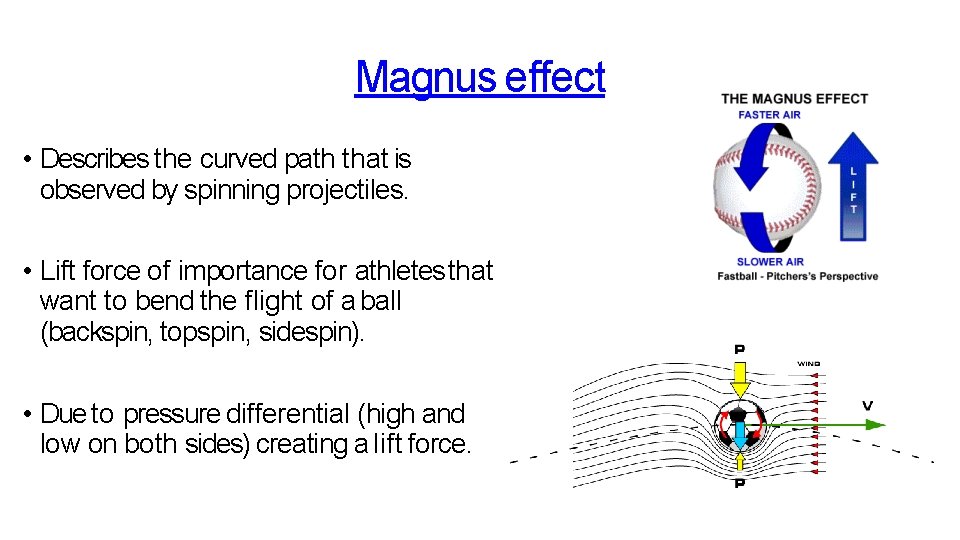
Magnus effect • Describes the curved path that is observed by spinning projectiles. • Lift force of importance for athletes that want to bend the flight of a ball (backspin, topspin, sidespin). • Due to pressure differential (high and low on both sides) creating a lift force.

Baseball Knuckleballs • It is well known that greasing, cutting, scuffing, or wetting the surface of the ball can produce the strange antics of the knuckleball. A ball that has been treated in this manner will act as a knuckleball but at a faster speed. In a sport already dominated by the pitcher, this strategy gave the pitcher further advantage and as a result has been outlawed. • All the pitches thrown in baseball are affected in one way or another by environmental conditions. As a generalization, dense air helps move the ball around, whereas thin air at high altitudes makes it easy for the ball to go faster. Knuckleballs become less deceptive at high altitudes and as temperature rises. In these conditions, the game belongs to the slugger and the fastball pitcher.

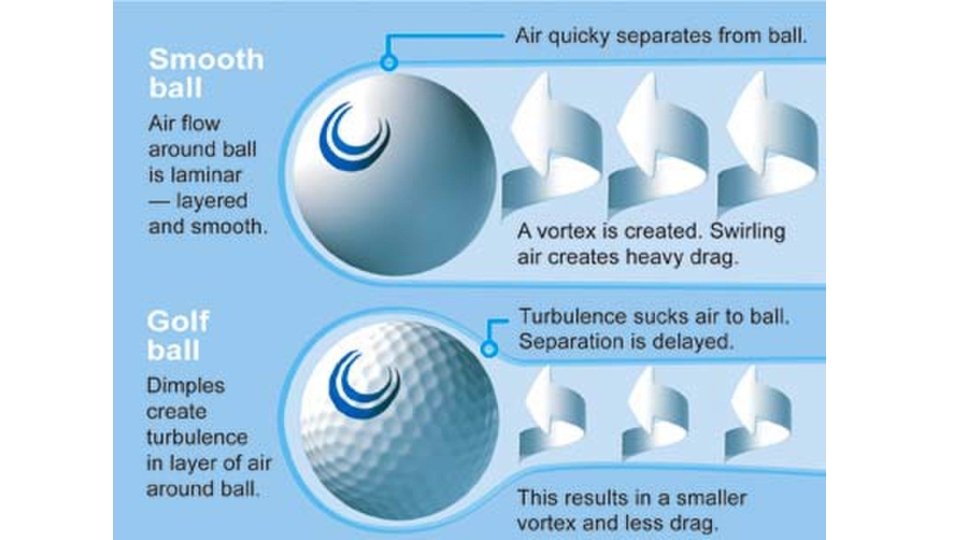
Why do golf balls have dimples? • Originally the were smooth, but over time they became damaged with bumps and nicks. • Observed these nicks and bumps actually made the ball go farther…but why? • These induced turbulence (mixed airflow) in the layer (boundary layer) of air next to the ball which reduces drag. • At high speeds (golf balls), adding dimples creates these layers of air to “cling” to the ball as long as possible.