4 3 Covariance Correlation 1 Covariance Definition 4


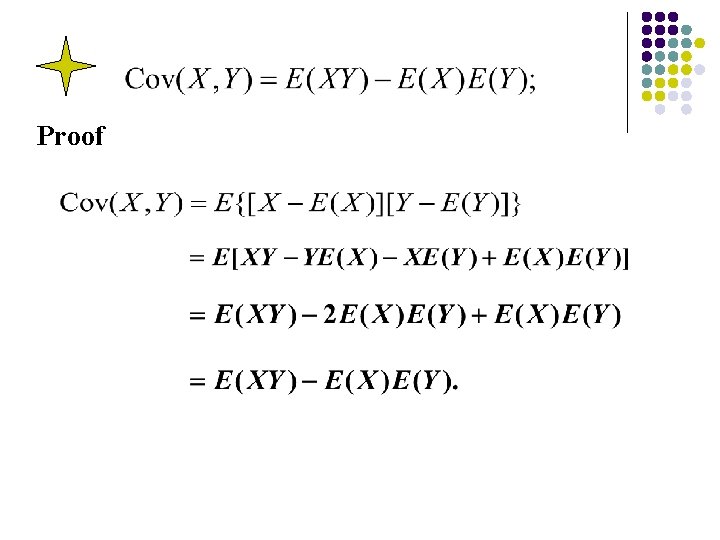



![(3) Cov(X+Y,Z)=Cov(X, Z)+Cov(Y, Z); Proof Cov(X+Y,Z)= E[(X+Y)Z]-E(X+Y)E(Z) =E(XZ)+E(YZ)-E(X)E(Z)-E(Y)E(Z) =Cov(X, Z)+Cov(Y, Z) (4) D(X+Y)=D(X)+D(Y)+2 Cov(X, (3) Cov(X+Y,Z)=Cov(X, Z)+Cov(Y, Z); Proof Cov(X+Y,Z)= E[(X+Y)Z]-E(X+Y)E(Z) =E(XZ)+E(YZ)-E(X)E(Z)-E(Y)E(Z) =Cov(X, Z)+Cov(Y, Z) (4) D(X+Y)=D(X)+D(Y)+2 Cov(X,](https://slidetodoc.com/presentation_image_h/976b381edf14202d5f8451e9977e1a68/image-7.jpg)


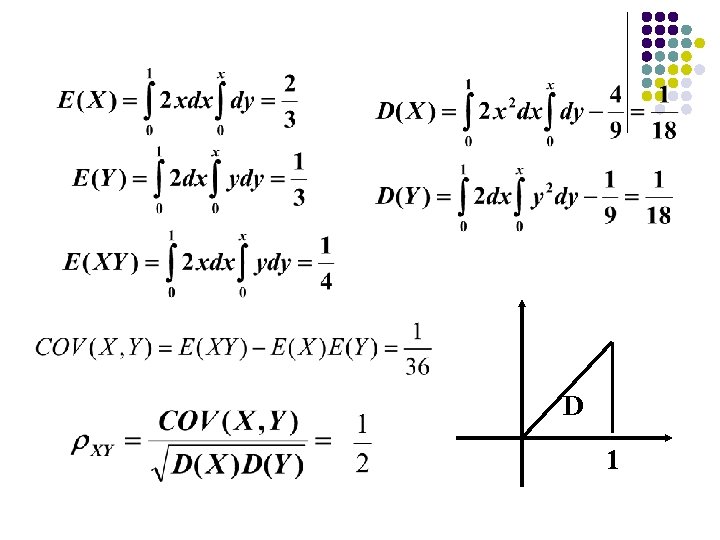




- Slides: 14

4. 3 Covariance � Correlation

1. Covariance Definition 4. 3 That is to say If X and Y are discrete random variables, If X and Y are continuous random variables,
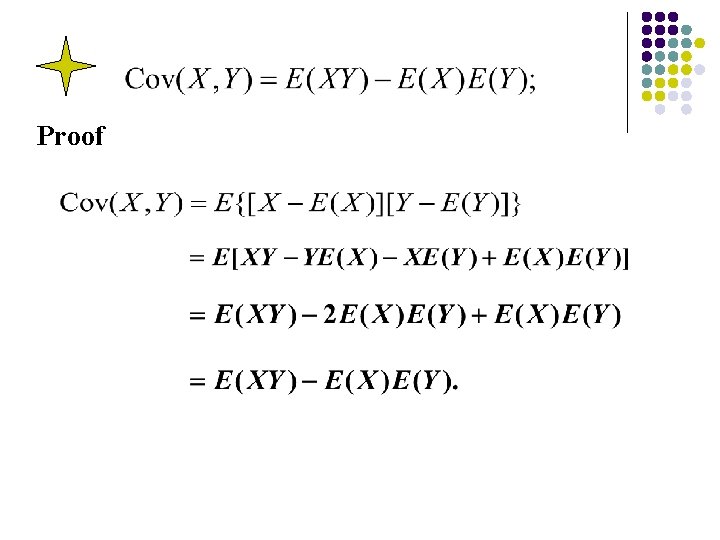
Proof

Example Suppose that (X, Y) is uniformly distributed on D={(X, Y):x 2+y 2 1}. Prove that X and Y are uncorrelated but not independent. Proof

Thus X and Y are uncorrelated. Since Thus, X is not independent of Y.

2. Properties of covariance: P 82 (1) Cov(X, Y)=Cov(Y, X); (2) Cov(a. X, b. Y)=ab. Cov(X, Y), where a, b are constants Proof Cov(a. X, b. Y)=E(a. Xb. Y)-E(a. X)E(b. Y) =ab. E(XY)-a. E(X)b. E(Y) =ab[E(XY)-E(X)E(Y)] =ab. Cov(X, Y)
![3 CovXYZCovX ZCovY Z Proof CovXYZ EXYZEXYEZ EXZEYZEXEZEYEZ CovX ZCovY Z 4 DXYDXDY2 CovX (3) Cov(X+Y,Z)=Cov(X, Z)+Cov(Y, Z); Proof Cov(X+Y,Z)= E[(X+Y)Z]-E(X+Y)E(Z) =E(XZ)+E(YZ)-E(X)E(Z)-E(Y)E(Z) =Cov(X, Z)+Cov(Y, Z) (4) D(X+Y)=D(X)+D(Y)+2 Cov(X,](https://slidetodoc.com/presentation_image_h/976b381edf14202d5f8451e9977e1a68/image-7.jpg)
(3) Cov(X+Y,Z)=Cov(X, Z)+Cov(Y, Z); Proof Cov(X+Y,Z)= E[(X+Y)Z]-E(X+Y)E(Z) =E(XZ)+E(YZ)-E(X)E(Z)-E(Y)E(Z) =Cov(X, Z)+Cov(Y, Z) (4) D(X+Y)=D(X)+D(Y)+2 Cov(X, Y). Remark D(X-Y)=D[X+(-Y)]=D(X)+D(Y)-2 Cov(X, Y) Example 4. 15 ----P 84

3. Correlation Coefficients Definition 4. 4 Suppose that r. v. X,Y has finite variance, dentoed by DX>0, DY>0,respectively, then, is name the correlation coefficients of r. v. X and Y.

Properties of coefficients (1) | XY| 1; (2) | XY|=1 There exists constants a, b such that P {Y= a. X+b}=1; (3) X and Y are uncorrelated XY; 1. Suppose that (X, Y) are uniformly distributed on D: 0<x<1, 0<y<x, try to determine the coefficient of X and Y. x=y Answer D 1
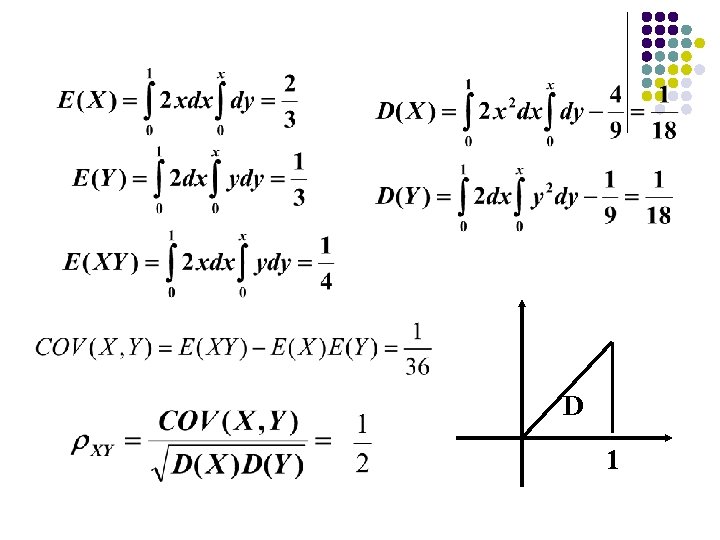
D 1

Answer 1) 2) What does Example 2 indicate?

Proof

Note P 86 Thus, if (X,Y)follow two-dimensional distribution, then “X and Y are independent” is equvalent to “X and Y are uncorrelated

Example 4. 16— 4. 18 (P 86) Exercise: P 90— 11 Find Cov(X, Y), 12 Homework: P 91— 16, 17
 Covariance correlation
Covariance correlation Covariance properties
Covariance properties Correlation covariance
Correlation covariance Positive correlation versus negative correlation
Positive correlation versus negative correlation Positive versus negative correlation
Positive versus negative correlation Cov x,y
Cov x,y Définition de la covariance
Définition de la covariance Mars red
Mars red Covariance between two random variables
Covariance between two random variables Covariance formula
Covariance formula Covariance formule
Covariance formule Covariance properties
Covariance properties Discrete
Discrete Julia covariance matrix
Julia covariance matrix Covariance of two time series
Covariance of two time series