4 3 Counting Techniques Prob Stats Tree Diagrams

4. 3 Counting Techniques Prob & Stats

Tree Diagrams n When calculating probabilities, you need to know the total outcomes number of _______ in the _______. sample space

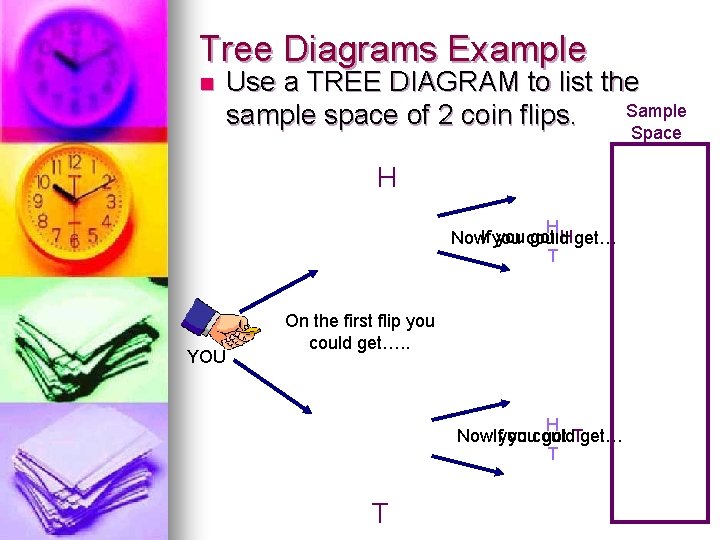
Tree Diagrams Example n Use a TREE DIAGRAM to list the Sample space of 2 coin flips. Space H H you could got H get… Now. If you T YOU On the first flip you could get…. . H Now. Ifyou youcould got Tget… T T

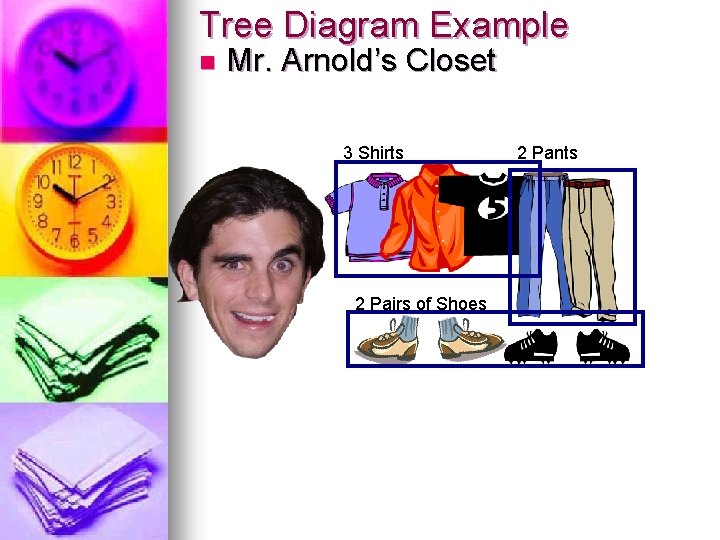
Tree Diagram Example n Mr. Arnold’s Closet 3 Shirts 2 Pairs of Shoes 2 Pants

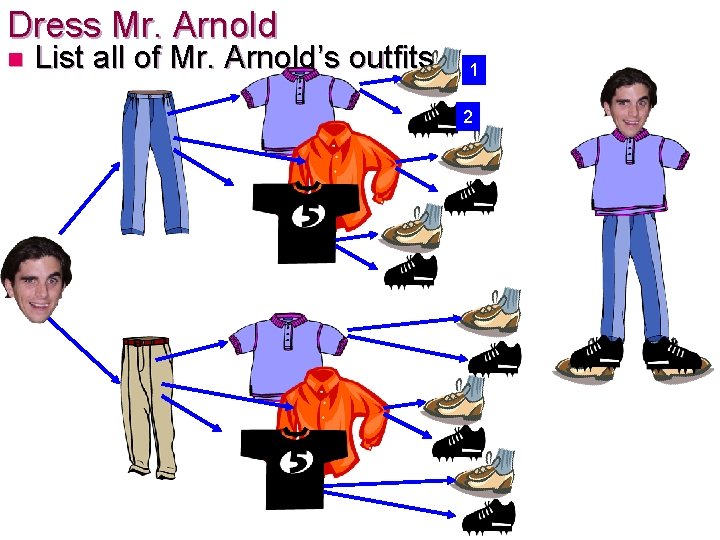
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2

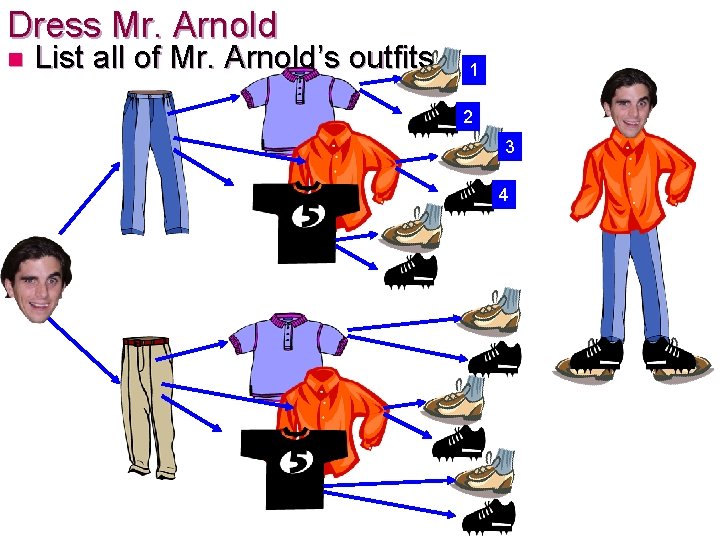
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2 3 4

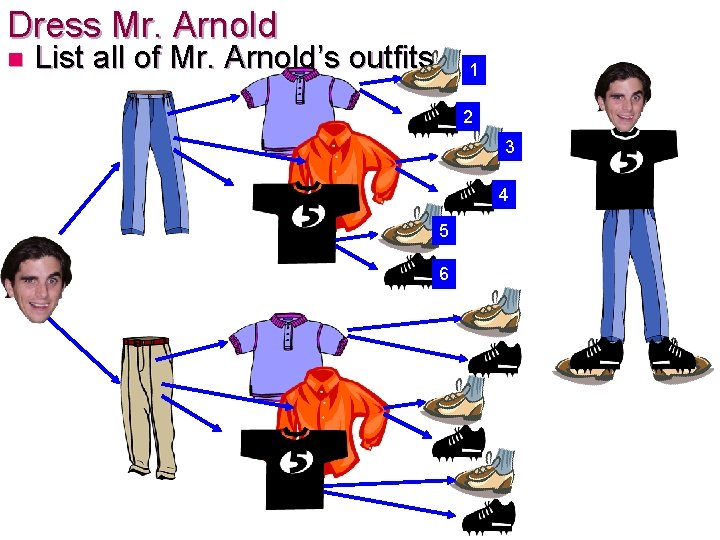
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2 3 4 5 6

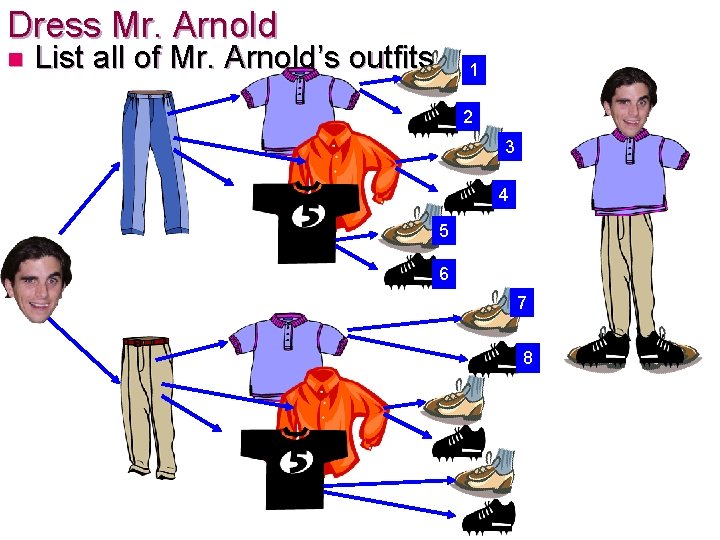
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2 3 4 5 6 7 8

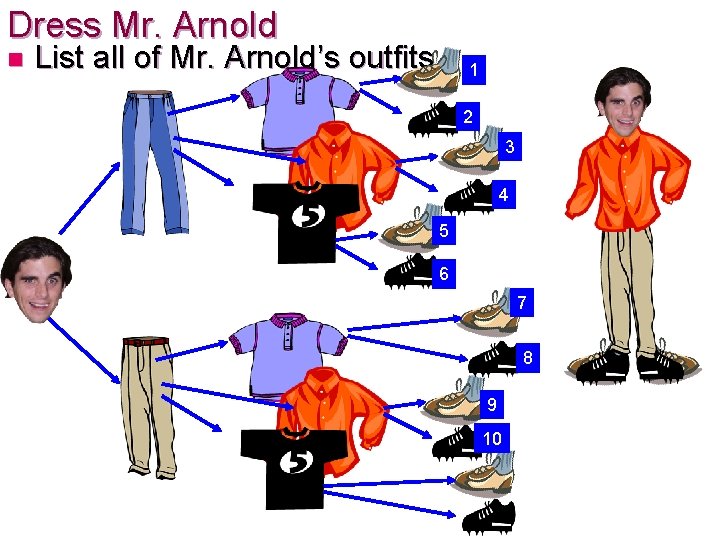
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2 3 4 5 6 7 8 9 10

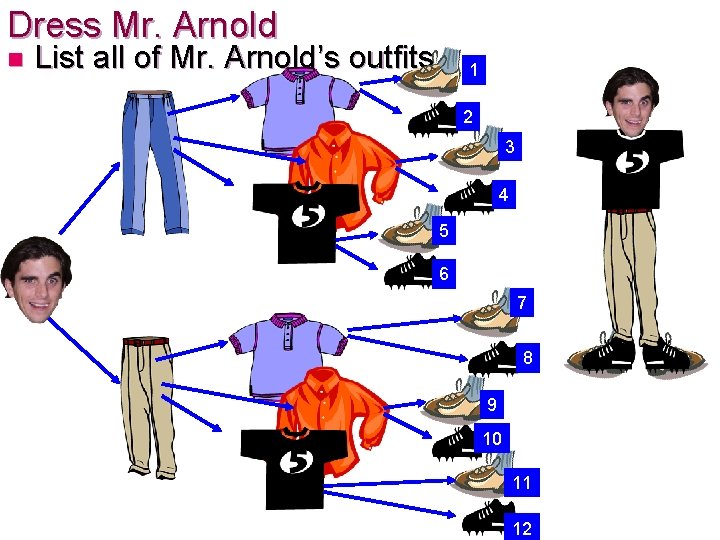
Dress Mr. Arnold n List all of Mr. Arnold’s outfits 1 2 3 4 5 6 7 8 9 10 11 12

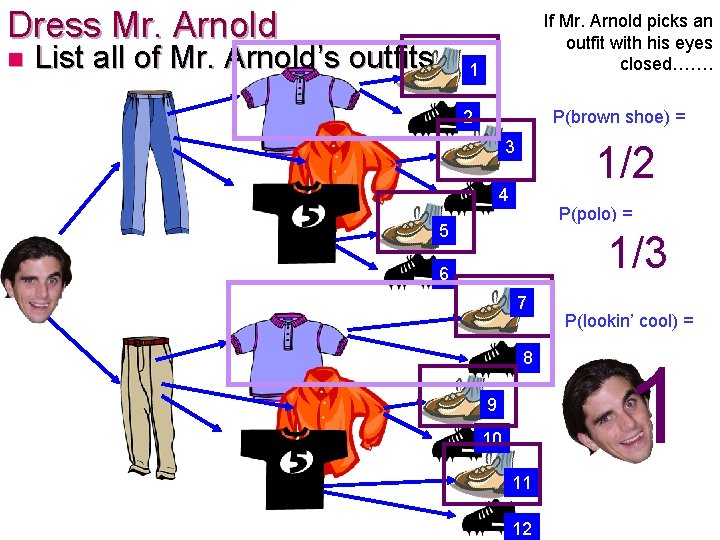
Dress Mr. Arnold n List all of Mr. Arnold’s outfits If Mr. Arnold picks an outfit with his eyes closed……. 1 2 P(brown shoe) = 6/12 1/2 3 4 P(polo) = 5 1/3 4/12 6 7 8 9 10 11 12 P(lookin’ cool) = 1

Multiplication Rule of Counting The size of the sample space is denominator of our the ______ probability n So we don’t always need to know what each outcome is, just the number of outcomes. n

Multiplication Rule of Compound Events If… n X = total number of outcomes for event A n Y = total number of outcomes for event B n Then number of outcomes for A times y followed by B = x_____

Multiplication Rule: Dress Mr. Arnold n Mr. Reed had 3 EVENTS 2 shoes 2 pants 3 shirts How many outcomes are there for EACH 2(2)(3) = 12 EVENT? OUTFITS

Permutations n Sometimes we are concerned with how many ways a group of arranged objects can be _____. • How many ways to arrange books on a shelf • How many ways a group of people can stand in line • How many ways to scramble a word’s letters

Example: 3 People, 3 Chairs Wonder Woman driving n n n Wonder Woman’s invisible plane has 3 chairs. There are 3 people who need a lift. How many seating options are there? of each chair as 6 Think Seating Options! an EVENT 3 2 1 How many ways the Now that thethe first 1 st 2 could is are filled? filled. st chair be filled? 1 many 3(2)(1) = options 6 ways OPTIONS How many to forfill 2 nd 3 rd ? ? Superman driving Batman driving

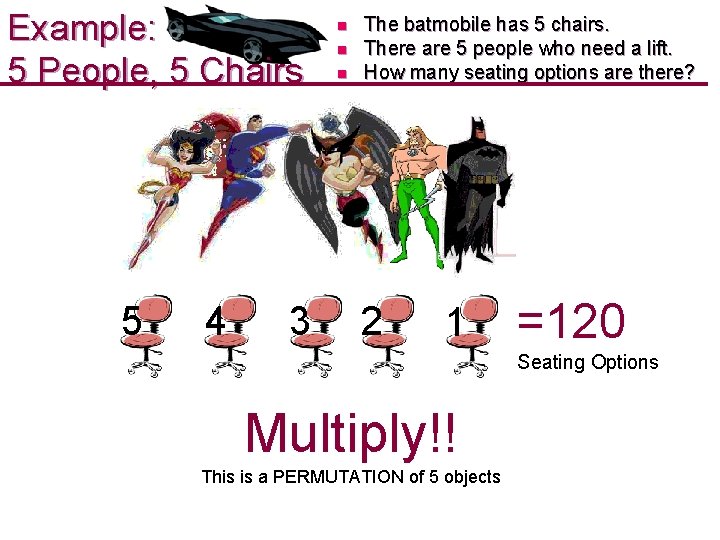
Example: 5 People, 5 Chairs 5 4 3 n n n The batmobile has 5 chairs. There are 5 people who need a lift. How many seating options are there? 2 1 =120 Seating Options Multiply!! This is a PERMUTATION of 5 objects

Commercial Break: FACTORIAL n n denoted with ! 5! Multiply all integers ≤ the number n 5! = 5(4)(3)(2)(1) = 120 0! = 1 1! = 1 n Calculate 6! n What is 6! / 5!? n 6! = 6(5)(4)(3)(2)(1) = 720

Commercial Break: FACTORIAL n n denoted with ! 5! Multiply all integers ≤ the number n 0! = 1 1! = 1 Calculate 6! n What is 6! / 5!? n n 6(5)(4)(3)(2)(1) 5(4)(3)(2)(1) =6

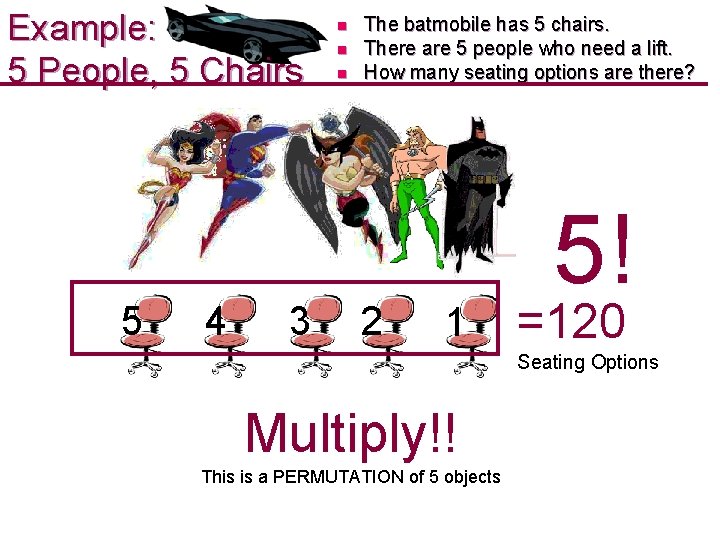
Example: 5 People, 5 Chairs 5 4 3 n n n The batmobile has 5 chairs. There are 5 people who need a lift. How many seating options are there? 2 1 5! =120 Seating Options Multiply!! This is a PERMUTATION of 5 objects

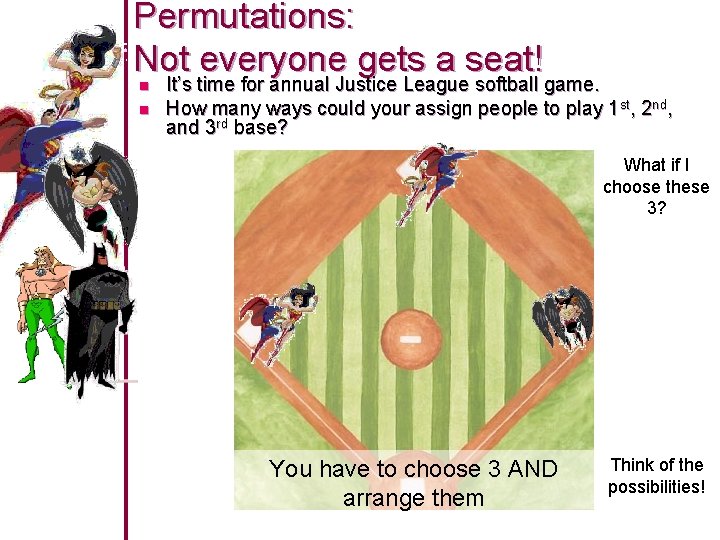
Permutations: Not everyone gets a seat! n n It’s time for annual Justice League softball game. How many ways could your assign people to play 1 st, 2 nd, and 3 rd base? What if I choose these 3? You have to choose 3 AND arrange them Think of the possibilities!

Permutations: Not everyone gets a seat! n n It’s time for annual Justice League softball game. How many ways could your assign people to play 1 st, 2 nd, and 3 rd base? BUT… What if I choose THESE 3? You have to choose 3 AND arrange them Think of the possibilities!

Permutations: Not everyone gets a seat! n n It’s time for annual Justice League softball game. How many ways could your assign people to play 1 st, 2 nd, and 3 rd base? BUT… What if I choose THESE 3? This is going to take FOREVER You have to choose 3 AND arrange them Think of the possibilities!

You have 3 EVENTS? n How many outcomes for each event How many outcomes for this event! 5 You have to choose 3 AND arrange them

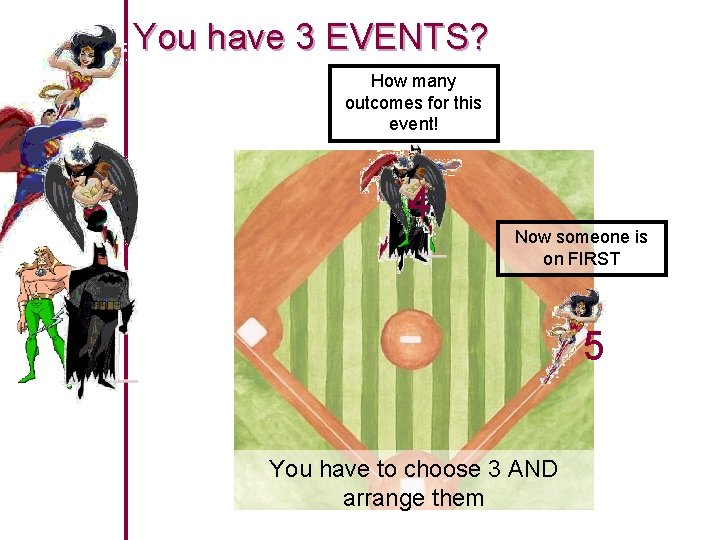
You have 3 EVENTS? How many outcomes for this event! 4 Now someone is on FIRST 5 You have to choose 3 AND arrange them

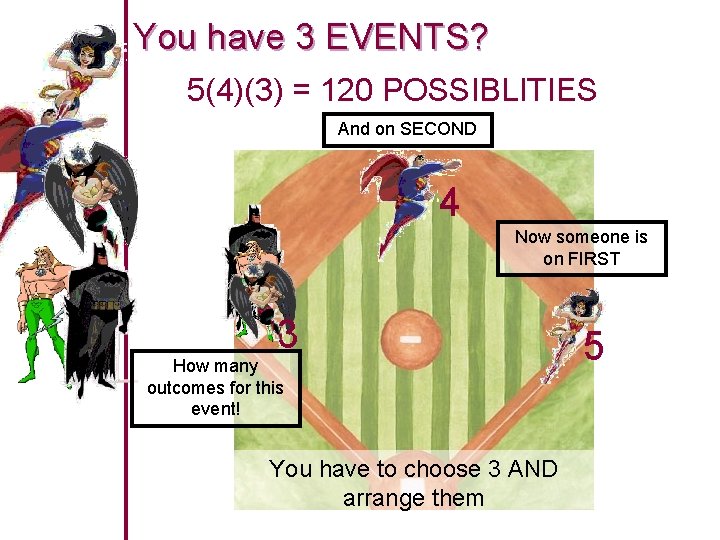
You have 3 EVENTS? 5(4)(3) = 120 POSSIBLITIES And on SECOND 4 Now someone is on FIRST 3 How many outcomes for this event! You have to choose 3 AND arrange them 5

Permutation Formula You have n objects n You select r objects n This is the number of ways you could select and arrange in order: n Another common notation for a permutation is n. Pr

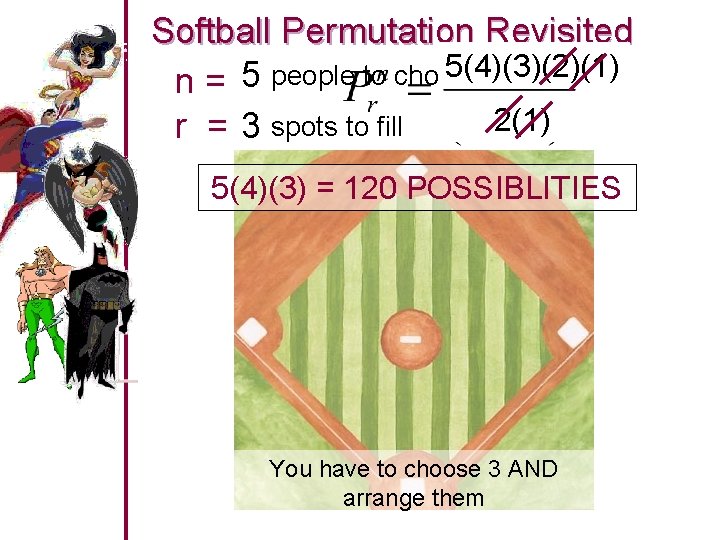
Softball Permutation Revisited 5! 5(4)(3)(2)(1) people to choose from 5 n= 2! 3)! r = 3 spots to fill (5 – 2(1) 5(4)(3) = 120 POSSIBLITIES You have to choose 3 AND arrange them

Combinations Sometimes, we are only concerned with selecting a group and not the order in which they are selected. n A combination gives the number of ways to select a sample of r objects from a group of size n. n

Combination: Duty Calls There is an evil monster threatening the city. n The mayor calls the Justice League. n He requests that 3 members be sent to combat the menace. n The Justice League draws 3 names out of a hat to decide. n Does it matter who is selected first? NOPE n n Does it matter who is selected last? NOPE

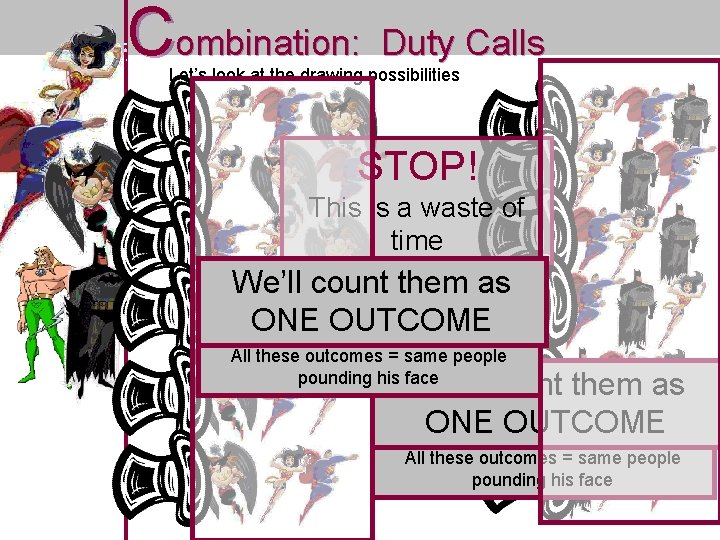
Combination: Duty Calls Let’s look at the drawing possibilities STOP! This is a waste of time These count are all the SAME: We’ll them as The monster doesn’t care who got drawn first. ONE OUTCOME All these outcomes = same people pounding his face These are all the SAME: The monster doesn’t care who got drawn first. We’ll count them as ONE OUTCOME All these outcomes = same people pounding his face

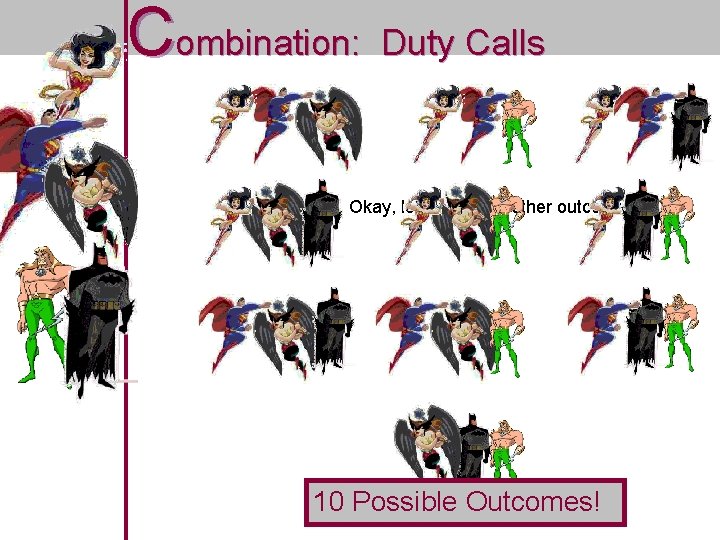
Combination: Duty Calls Okay, let’s consider other outcomes 10 Possible Outcomes!

Combination Formula You have n objects n You want a group of r objects n You DON’T CARE what order they are selected in n Combinations are also denoted n. Cr Read “n choose r”

Duty Calls: Revisited to choose from n = 5 people ORDER DOESN’T MATTER r = 3 spots to fill 5(4)(3)(2)(1) 5! 3(2)(1) 3!(2)! 3!(5 - 3)! 10 Possible Outcomes! Now we can go save the city 20 2

Permutation vs. Combination Order matters Permutation n Order doesn’t matter Combination n