4 24 Factor each quadratic expression below if

4 -24. Factor each quadratic expression below, if possible. Use a Diamond Problem and area model for each one. 2 a. x + 6 x + 9 2 b. 2 x + 5 x + 3 2 c. x + 5 x − 7 2 d. 3 m + m − 14 1=a, 2=b, 3=c, 4=d Share

4. 1. 3 Factoring More Quadratics October 31, 2019 HW: 4 -28 through 4 -33

Objectives �CO: SWBAT factor quadratic expressions with missing terms, quadratic expressions that are not in standard form, and quadratic expressions with more than one possible factored form. �LO: SWBAT explain how to factor to their team.

4 -25. You have been working with quadratic expressions written in the form ax 2 + bx + c. But what if a term is missing? Or what if the terms are in a different order? Consider these questions while you factor the expressions below. Share your ideas with your teammates and be prepared to demonstrate your process for the class. a. 9 x 2 + 0 x − 4 2 − 16 x + 0 2 b. 12 x − 16 x 2 – 10 k + 3 2 c. 8 k c. 3 + 8 k – 10 k d. 40 – 100 m d. Not quadratic (use greatest common factor) a. 9 x 2 Team: #3 s can get hints

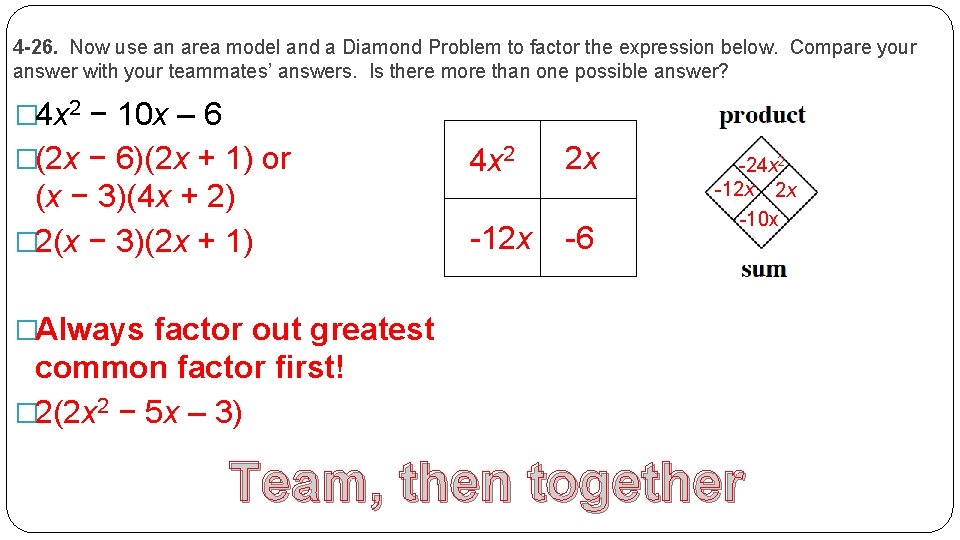
4 -26. Now use an area model and a Diamond Problem to factor the expression below. Compare your answer with your teammates’ answers. Is there more than one possible answer? � 4 x 2 − 10 x – 6 �(2 x − 6)(2 x + 1) or 4 x 2 2 x (x − 3)(4 x + 2) � 2(x − 3)(2 x + 1) -12 x -6 -24 x 2 -12 x 2 x -10 x �Always factor out greatest common factor first! � 2(2 x 2 − 5 x – 3) Team, then together