4 2 Trig Functions The Unit Circle I

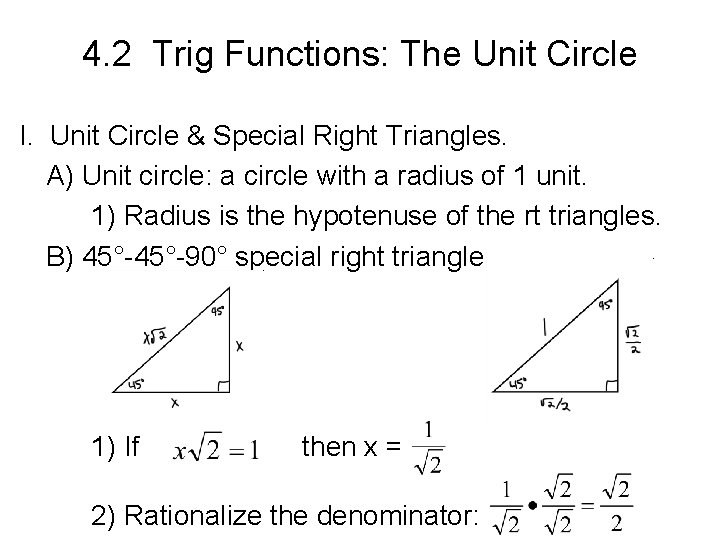
4. 2 Trig Functions: The Unit Circle I. Unit Circle & Special Right Triangles. A) Unit circle: a circle with a radius of 1 unit. 1) Radius is the hypotenuse of the rt triangles. B) 45°-90° special right triangle. 1) If then x = 2) Rationalize the denominator:

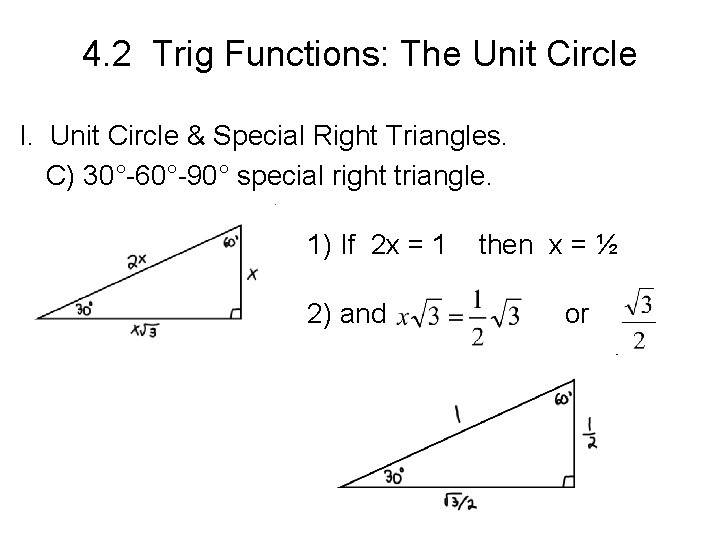
4. 2 Trig Functions: The Unit Circle I. Unit Circle & Special Right Triangles. C) 30°-60°-90° special right triangle. 1) If 2 x = 1 2) and then x = ½ or

4. 2 Trig Functions: The Unit Circle II. The Unit Circle and reference angles. A) The unit circle is the equation: x 2 + y 2 = 1. B) If you drew all the 30 -60 -90 and 45 -45 -90 special triangles in each quadrant of the unit circle, you would get all the “special” reference angles of the unit circle. 1) Divide the circle into 30° slices and you get all the 30 -60 -90 special right triangles (π/6). 2) Divide the circle into 45° slices and you get all the 45 -45 -90 special right triangles (π/4).

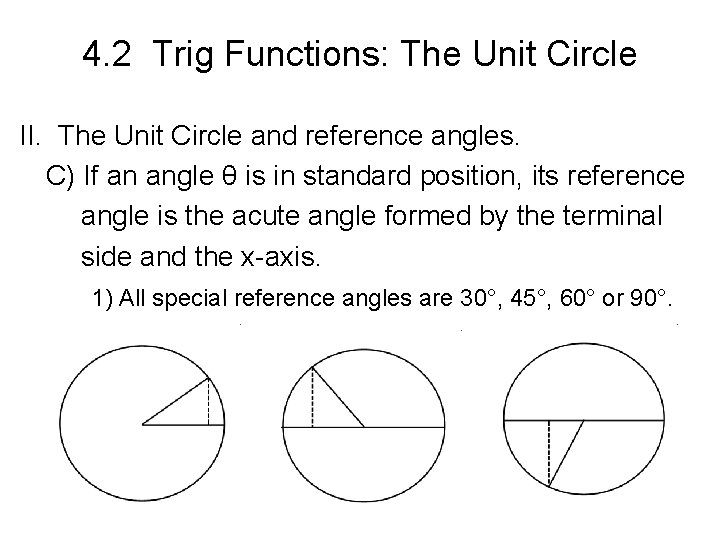
4. 2 Trig Functions: The Unit Circle II. The Unit Circle and reference angles. C) If an angle θ is in standard position, its reference angle is the acute angle formed by the terminal side and the x-axis. 1) All special reference angles are 30°, 45°, 60° or 90°.

4. 2 Trig Functions: The Unit Circle II. The Unit Circle and reference angles. D) Each reference angle forms a special right triangle whose width (x distance) and height (y distance) can be calculated using the unit circle. 1) These lengths form the (x, y) coordinate point where the terminal ray touches the unit circle. 2) For all the special right triangles, these lengths are… a) 0, 1, – 1 for 90° angles (0°, 90°, 180°, 270°, 360°). b) 0, 1, – 1, c) 0, 1, – 1, for 45° angles (0°, 45°, 90°, etc) for 30° angles (0°, 30°, 60°etc)