4 2 Triangle Congruence by SSS SAS Essential

4. 2 Triangle Congruence by SSS & SAS Essential Question: How do you prove triangles are congruent using the SSS and SAS postulates?

• We know, if two triangles have three pairs of congruent corresponding angles and three pairs of congruent corresponding sides, then the triangles are congruent. • However, you do not need to know that all six corresponding parts are congruent in order to conclude that two triangles are congruent. • You can use some of the corresponding parts to deduce the same must be true for the rest of the parts.

• Postulate 4 -1 • Side-Side (SSS) Postulate – If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent. – ΔGHF ≅ ΔPQR G H F P Q R

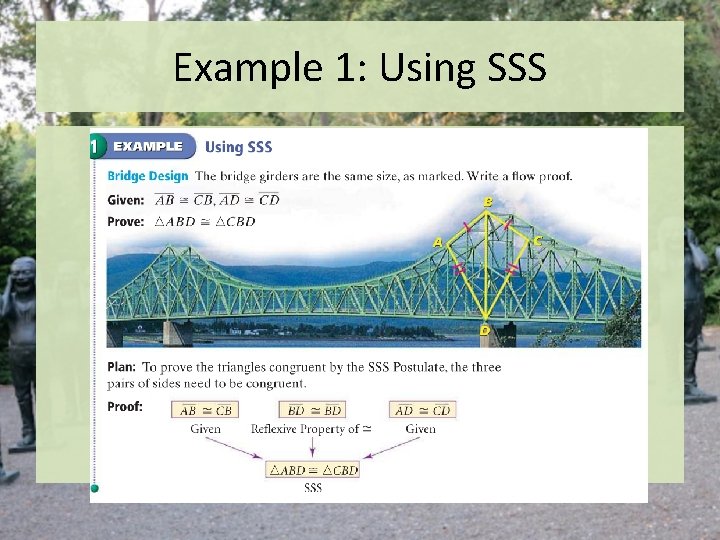
Example 1: Using SSS

Practice • Given: HF ≅ HJ, FG ≅ JK. H is the midpoint of GK. F J • Prove: ΔFGH ≅ ΔJKH G H K

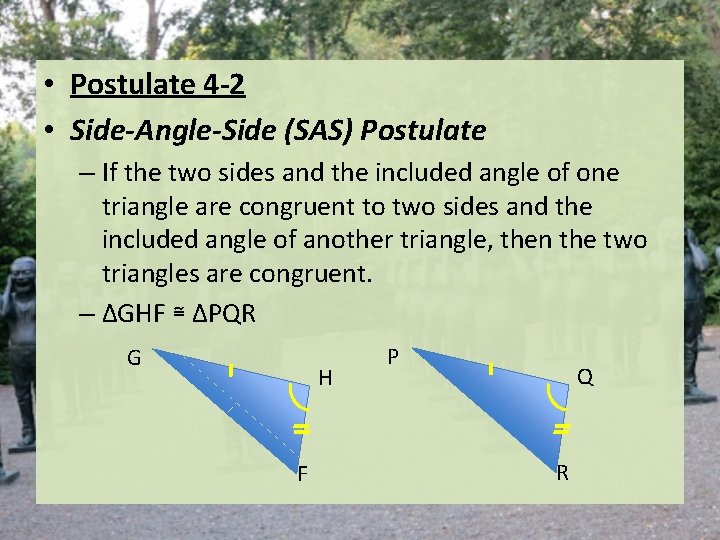
• Postulate 4 -2 • Side-Angle-Side (SAS) Postulate – If the two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. – ΔGHF ≅ ΔPQR G H F P Q R

Example 2: Using SAS

Practice • What other information do you need to prove A ΔABC ≅ ΔCDA by SAS? 7 8 6 D 7 C B

Practice • What other information do you need to prove ΔABC ≅ ΔCDA by SAS? A D B C

Example 3: Congruent?

Practice

Summary • Answer the essential question in complete, detailed sentences. • How do you prove triangles are congruent using the SSS and SAS postulates? • Write 2 -4 study questions in the left column that correspond with the notes.