4 2 Patterns and Linear Functions Dependent Variable

4. 2 Patterns and Linear Functions: Dependent Variable: The variable that depends upon the value of another. Independent Variable: The variable that is not dependent. Input: The values of the independent variable. Output: The values of the dependent variable.

Function f(x): A relationship that pairs one input to exactly one output (x, y) Linear Function: A function whose graph is a nonvertical line or part of a nonvertical line.

GOAL:

In math we use tables, words, equations, set of ordered pairs and graphs to represent a relationship between two variables. This can be done when we are presented with the following: 1. Geometric Relationships, 2. Linear Functions

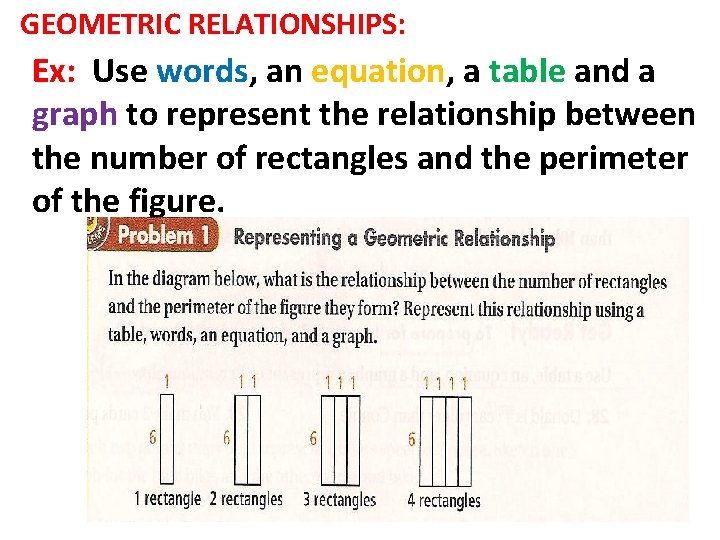
GEOMETRIC RELATIONSHIPS: Ex: Use words, an equation, a table and a graph to represent the relationship between the number of rectangles and the perimeter of the figure.

Words: Look at the figure, multiply the number of rectangles by 2 to get the total lengths of the top an bottom sides of the combined figure. Then add 2 times the length of the left and right sides of the combined figure to obtain the final answer for the total perimeter of the figure.

Equation: Look at the figure: We must realize that the only thing that is changing is the number of the short side (width). Also, the number of the length is constant which is = 12. Using this info we see that the equation is: y or f(x) = twice the number of short + twice the length. f(x) = 2 x + 12

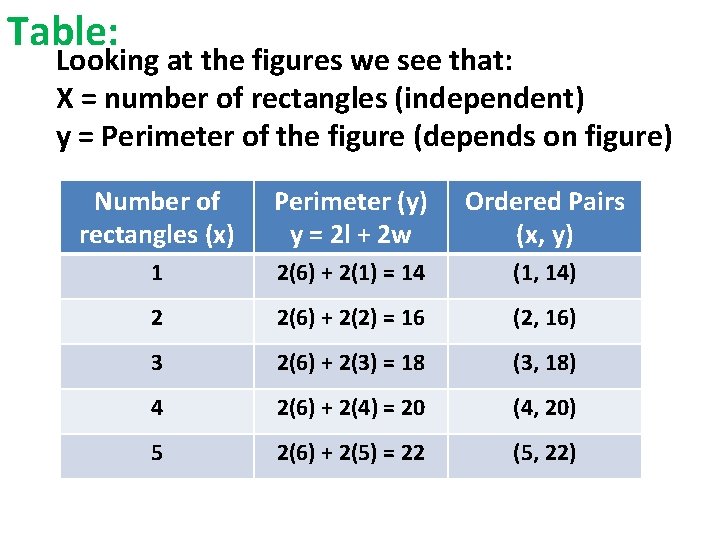
Table: Looking at the figures we see that: X = number of rectangles (independent) y = Perimeter of the figure (depends on figure) Number of rectangles (x) Perimeter (y) y = 2 l + 2 w Ordered Pairs (x, y) 1 2(6) + 2(1) = 14 (1, 14) 2 2(6) + 2(2) = 16 (2, 16) 3 2(6) + 2(3) = 18 (3, 18) 4 2(6) + 2(4) = 20 (4, 20) 5 2(6) + 2(5) = 22 (5, 22)

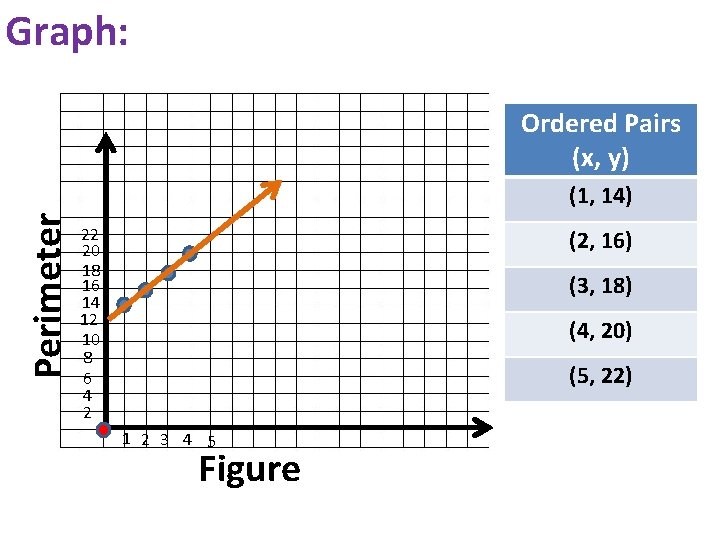
Graph: Ordered Pairs (x, y) Perimeter (1, 14) 22 20 18 16 14 12 10 8 6 4 2 (2, 16) (3, 18) (4, 20) (5, 22) 1 2 3 4 5 Figure

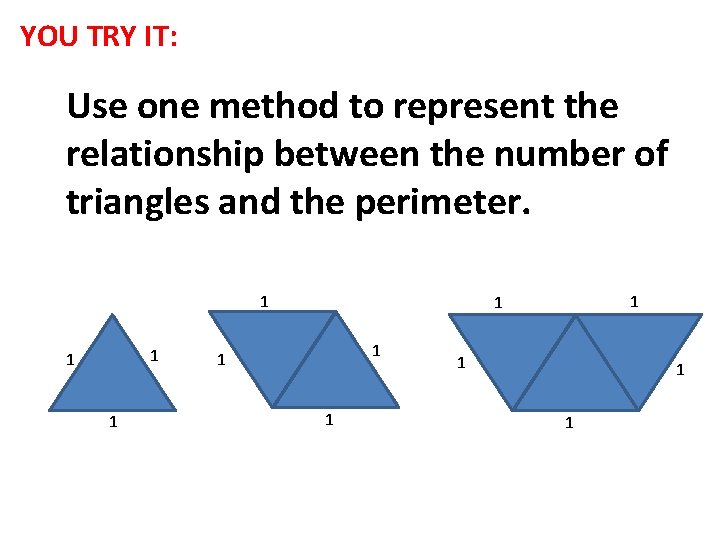
YOU TRY IT: Use one method to represent the relationship between the number of triangles and the perimeter. 1 1 1

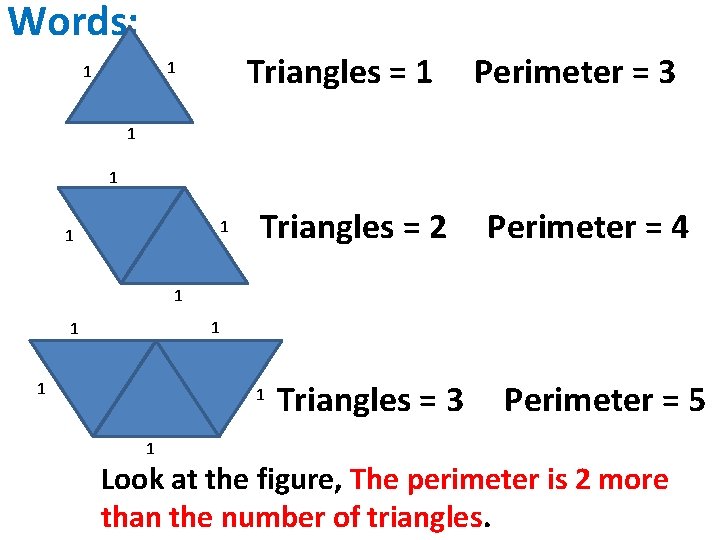
Words: Triangles = 1 1 1 Perimeter = 3 1 1 Triangles = 2 Perimeter = 4 1 1 1 Triangles = 3 Perimeter = 5 Look at the figure, The perimeter is 2 more than the number of triangles.

Equation: Again, the perimeter [ y or f(x)] is 2 more than the number of triangles (x) y =x+2 f(x) = x + 2

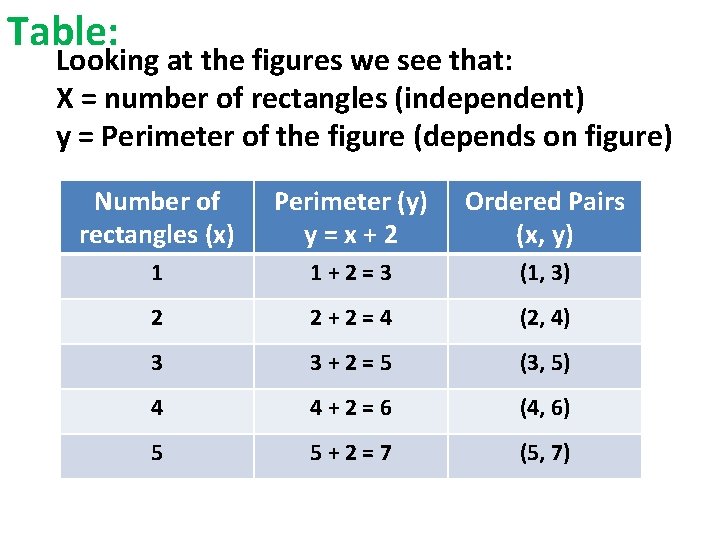
Table: Looking at the figures we see that: X = number of rectangles (independent) y = Perimeter of the figure (depends on figure) Number of rectangles (x) Perimeter (y) y=x+2 Ordered Pairs (x, y) 1 1+2=3 (1, 3) 2 2+2=4 (2, 4) 3 3+2=5 (3, 5) 4 4+2=6 (4, 6) 5 5+2=7 (5, 7)

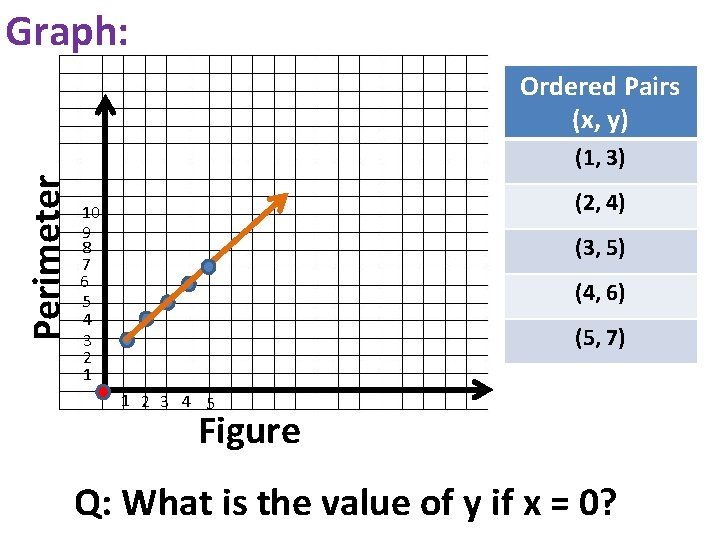
Graph: Ordered Pairs (x, y) Perimeter (1, 3) (2, 4) 10 9 8 7 6 5 4 3 2 1 (3, 5) (4, 6) (5, 7) 1 2 3 4 5 Figure Q: What is the value of y if x = 0?

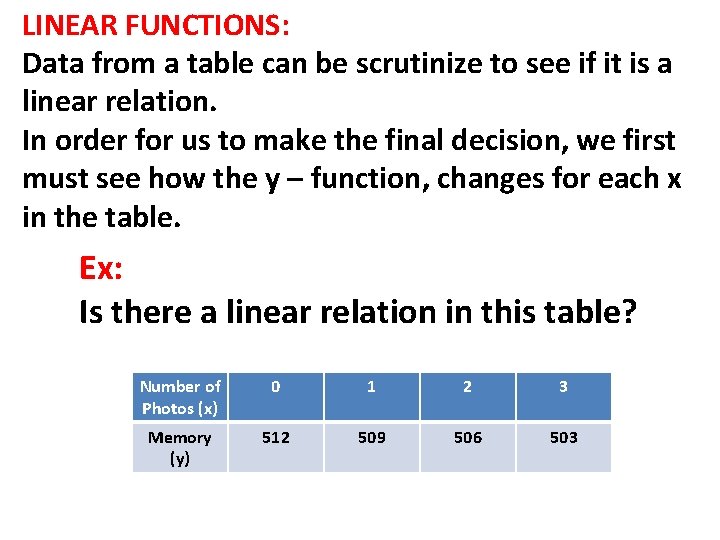
LINEAR FUNCTIONS: Data from a table can be scrutinize to see if it is a linear relation. In order for us to make the final decision, we first must see how the y – function, changes for each x in the table. Ex: Is there a linear relation in this table? Number of Photos (x) 0 1 2 3 Memory (y) 512 509 506 503

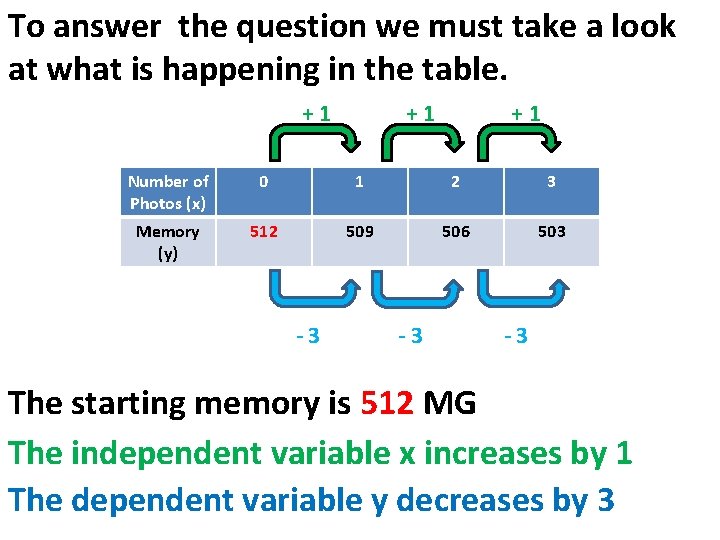
To answer the question we must take a look at what is happening in the table. +1 +1 +1 Number of Photos (x) 0 1 2 3 Memory (y) 512 509 506 503 -3 -3 -3 The starting memory is 512 MG The independent variable x increases by 1 The dependent variable y decreases by 3

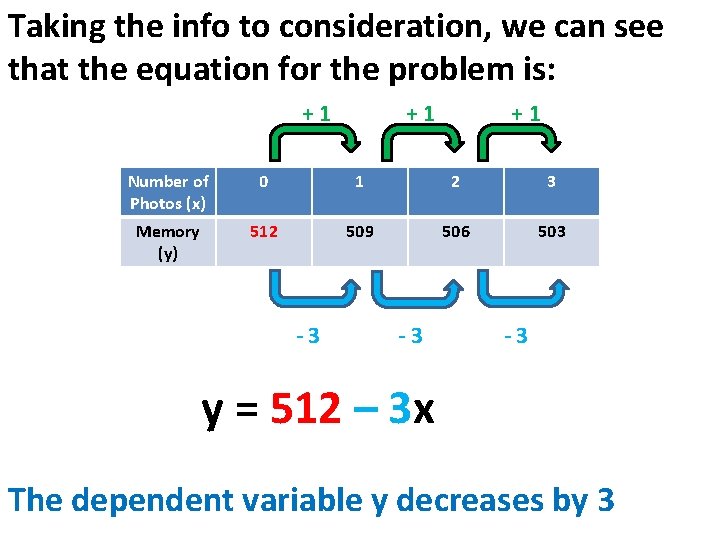
Taking the info to consideration, we can see that the equation for the problem is: +1 +1 +1 Number of Photos (x) 0 1 2 3 Memory (y) 512 509 506 503 -3 -3 -3 y = 512 – 3 x The dependent variable y decreases by 3

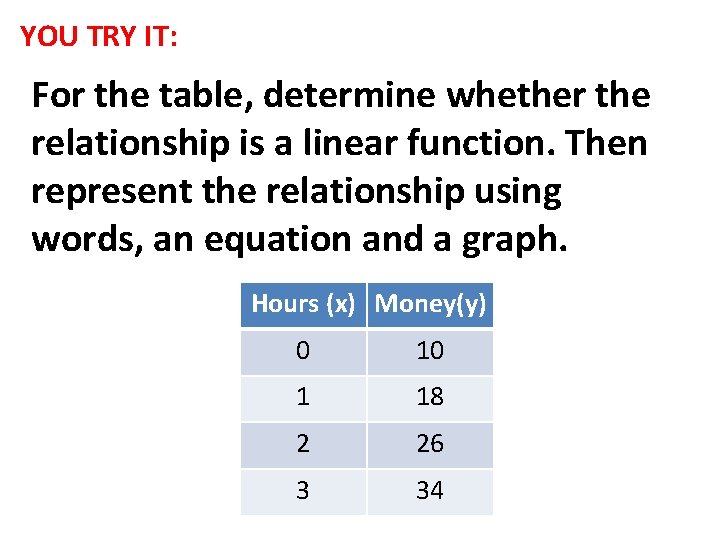
YOU TRY IT: For the table, determine whether the relationship is a linear function. Then represent the relationship using words, an equation and a graph. Hours (x) Money(y) 0 10 1 18 2 26 3 34

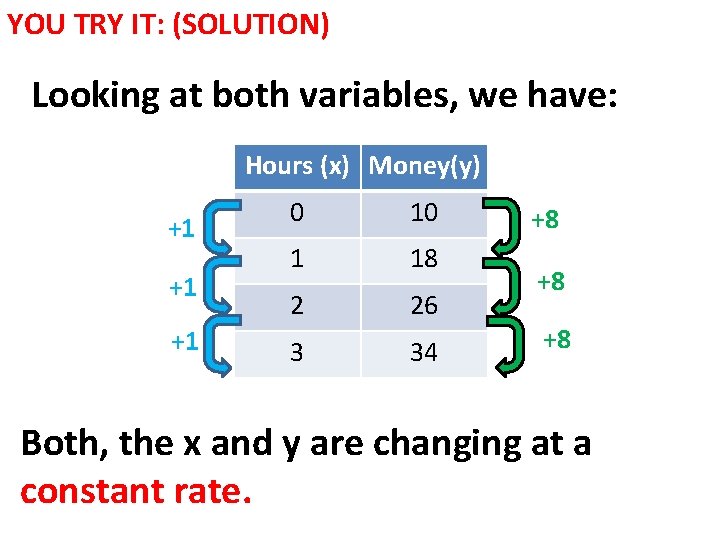
YOU TRY IT: (SOLUTION) Looking at both variables, we have: Hours (x) Money(y) +1 +1 +1 0 10 1 18 2 26 3 34 +8 +8 +8 Both, the x and y are changing at a constant rate.

YOU TRY IT: (Words Solution): A person had 10 dollars and then starts a job where he earns eight dollars per hour.

YOU TRY IT: (Equation Solution): We started with 10 dollars and earn 8 after each hour. y = 8 x + 10 f(x) = 8 x + 10

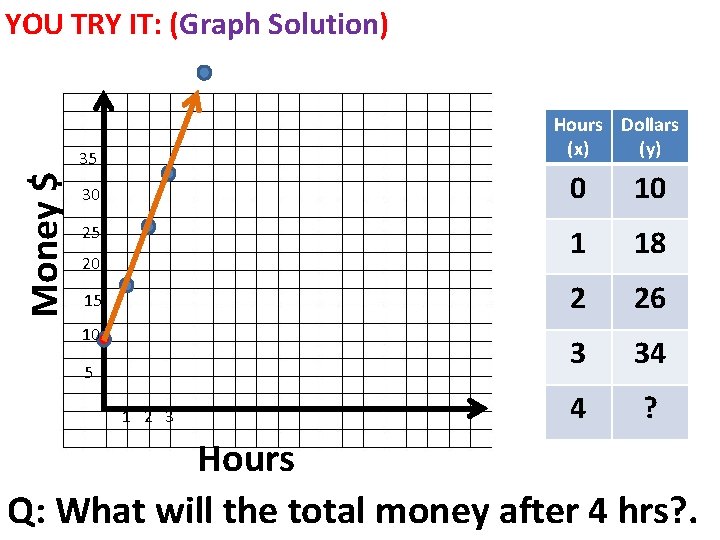
YOU TRY IT: (Graph Solution) Hours Dollars (x) (y) Money $ 35 30 25 20 15 10 5 1 2 3 0 10 1 18 2 26 3 34 4 ? Hours Q: What will the total money after 4 hrs? .

VIDEOS: Linear Functions https: //www. khanacademy. org/math/algebra/line ar-equations-and-inequalitie/analyzing-functionsalgebra/v/constructing-a-linear-function-wordproblem https: //www. khanacademy. org/math/algebra/line ar-equations-and-inequalitie/analyzing-functionsalgebra/v/constructing-and-interpreting-a-linearfunction

CLASS WORK: Pages: 243 – 245 Problems: As many as it takes to master the concept.

CLASSWORK: Page 243 -245 Problems: 5, 7, 9, 11, 12, 13, 14, 16, Review Handout