4 1 Probability Distributions Random Variables A random

§ 4. 1 Probability Distributions

Random Variables A random variable x represents a numerical value associated with each outcome of a probability distribution. A random variable is discrete if it has a finite or countable number of possible outcomes that can be listed. x 0 2 4 6 8 10 A random variable is continuous if it has an uncountable number of possible outcomes, represented by the intervals on a number line. x 0 2 4 6 8 10 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 2

Random Variables Example: Decide if the random variable x is discrete or continuous. a. ) The distance your car travels on a tank of gas The distance your car travels is a continuous random variable because it is a measurement that cannot be counted. (All measurements are continuous random variables. ) b. ) The number of students in a statistics class The number of students is a discrete random variable because it can be counted. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 3

Random Variables Checkpoint: Decide if the random variable x is discrete or continuous. a. ) The number of stocks in the Dow Jones Industrial Average that have share price increases on any given day The number of stocks whose share prices increase can be counted, so x it is a discrete variable b. ) The volume of bottled water in a 32 -ounce container The amount of water can be any volume between 0 and 32 ounces, so x is a continuous variable. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 4

Discrete Probability Distributions A discrete probability distribution lists each possible value the random variable can assume, together with its probability. A probability distribution must satisfy the following conditions. In Words In Symbols 1. The probability of each value of the discrete random variable is between 0 and 1, inclusive. 0 P (x) 1 2. The sum of all the probabilities is 1. ΣP (x) = 1 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 5

Verifying Probability Distributions Verify that the distribution is a probability distribution. Days of Probability rain, x P(x) 0 0. 216 1 0. 432 2 0. 288 3 0. 064 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 6

Probability Distribution Checkpoint Decide whether each distribution is a probability distribution. x P(x) 1 5 0. 28 6 0. 21 7 0. 43 2 3 4 8 0. 15 -1 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 7

Constructing a Discrete Probability Distribution Guidelines Let x be a discrete random variable with possible outcomes x 1, x 2, … , xn. 1. Make a frequency distribution for the possible outcomes. 2. Find the sum of the frequencies. 3. Find the probability of each possible outcome by dividing its frequency by the sum of the frequencies. 4. Check that each probability is between 0 and 1 and that the sum is 1. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 8

Graphing a Discrete Probability Distribution Guided Practice An industrial psychologist administered a personality inventory test for passive-aggressive traits to 150 employees. Individuals were rated on a score from 1 to 5, where 1 was extremely passive and 5 extremely aggressive. A score of 3 indicated neither trait. The results are shown in the table. Construct a probability distribution for the random variable x. Then graph the distribution using a histogram Score, x 1 2 3 4 5 Frequency, f 24 33 42 30 21 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 9

Passive-Aggressive Traits x 1 P (x) x f 1 2 3 4 24 33 42 30 5 21 Σf = 2 3 4 5 Σ P(x) = Larson & Farber, Elementary Statistics: Picturing the World, 3 e 10

Graphing a Discrete Probability Distribution Checkpoint A company tracks the number of sales new employees make each day during a 100 -day probationary period. The results for one new employee are shown. Construct and graph a probability distribution. Sales per Number day, x of days, f 0 16 1 19 2 3 4 5 6 7 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 15 21 9 10 8 2 11

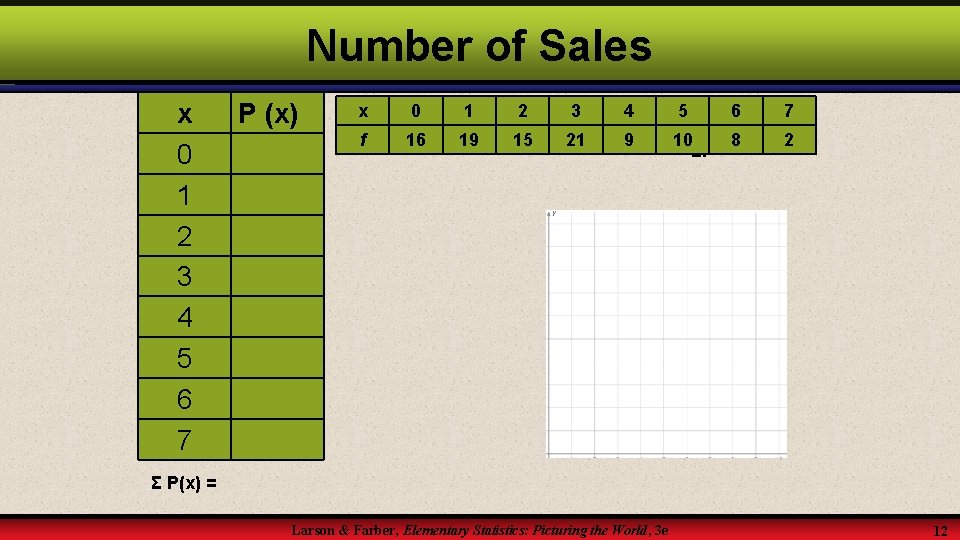
Number of Sales x 0 1 2 3 4 5 6 7 P (x) x 0 1 2 3 4 5 6 7 f 16 19 15 21 9 10 8 Σf = 2 Σ P(x) = Larson & Farber, Elementary Statistics: Picturing the World, 3 e 12

Mean The mean of a discrete random variable is given by μ = Σ x∙P(x). Each value of x is multiplied by its corresponding probability and the products are added. Example: Find the mean of the probability distribution for the sum of the two spins. x. P (x) x P (x) 2 0. 0625 2(0. 0625) = 0. 125 Σx. P(x) = 3. 5 3 0. 375 3(0. 375) = 1. 125 4 0. 5625 4(0. 5625) = 2. 25 The mean for the two spins is 3. 5. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 13

Finding the Mean of a Probability Distribution Calculate the mean x 1 2 3 P (x) 0. 16 0. 22 0. 28 4 5 0. 20 0. 14 Σ P(x) = x ∙ P (x) μ = Σ x ∙ P(x)= Larson & Farber, Elementary Statistics: Picturing the World, 3 e 14

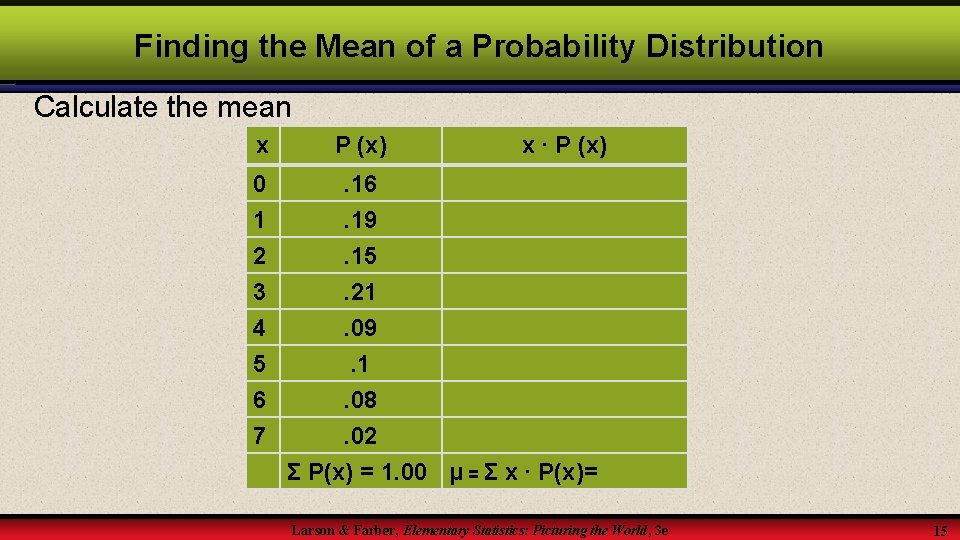
Finding the Mean of a Probability Distribution Calculate the mean x P (x) 0 . 16 1 2 . 19. 15 3 4 5 6 7 x ∙ P (x) . 21. 09. 1. 08. 02 Σ P(x) = 1. 00 μ = Σ x ∙ P(x)= Larson & Farber, Elementary Statistics: Picturing the World, 3 e 15

Variance The variance of a discrete random variable is given by 2 = Σ(x – μ)2 P (x). x 1 2 3 4 5 P (x) 0. 16 0. 22 0. 28 0. 20 0. 14 Σ P(x) = 1 x ∙ P (x) x-μ (x – μ)2 μ = Σ x ∙ P(x) = 2. 94 Larson & Farber, Elementary Statistics: Picturing the World, 3 e P(x) (x – μ)2 σ2 = Σ P(x) ∙ (x – μ)2 16

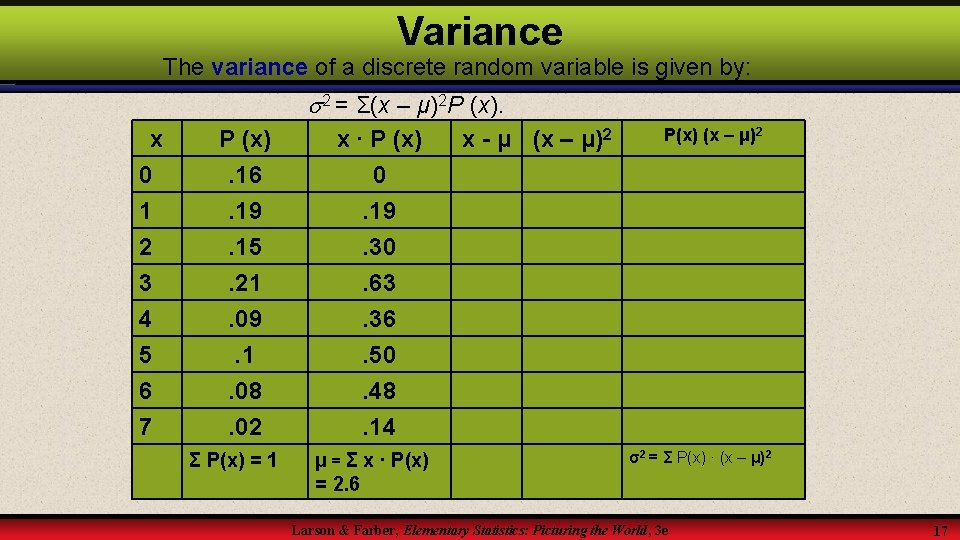
Variance The variance of a discrete random variable is given by: 2 = Σ(x – μ)2 P (x). x 0 1 2 3 4 5 6 7 P (x). 16. 19. 15. 21. 09. 1. 08. 02 Σ P(x) = 1 x ∙ P (x) 0. 19. 30. 63. 36. 50. 48. 14 μ = Σ x ∙ P(x) = 2. 6 x - μ (x – μ)2 P(x) (x – μ)2 σ2 = Σ P(x) ∙ (x – μ)2 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 17

Standard Deviation The standard deviation of a discrete random variable is given by σ = √ (Σ P(x) ∙ (x – μ)2) = Larson & Farber, Elementary Statistics: Picturing the World, 3 e 18

Expected Value The expected value of a discrete random variable is equal to the mean of the random variable. Expected Value = E (x) = μ = Σx. P(x). Example: At a raffle, 500 tickets are sold for $1 each for two prizes of $100 and $50. What is the expected value of your gain? Your gain for the $100 prize is $100 – $1 = $99. Your gain for the $50 prize is $50 – $1 = $49. Write a probability distribution for the possible gains (or outcomes). Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 19

Expected Value Example continued: At a raffle, 500 tickets are sold for $1 each for two prizes of $100 and $50. What is the expected value of your gain? Gain, x P (x) E(x) = Σx. P(x). $99 $49 –$1 Winning no prize Because the expected value is negative, you can expect to lose $0. 70 for each ticket you buy. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 20