4 1 Connectivity and Paths Cuts and Connectivity

4. 1 Connectivity and Paths: Cuts and Connectivity This copyrighted material is taken from Introduction to Graph Theory, 2 nd Ed. , by Doug West; and is not for further distribution beyond this course. These slides will be stored in a limited-access location on an IIT server and are not for distribution or use beyond Math 454/553. 1

Connectivity of Graphs Motivating Question How many vertices, or how many edges, can be deleted from a graph while keeping it connected? Applications (vertex connectivity) §Robustness of supercomputers to failures of processor nodes §Sensor networks’ resistance to individual sensor failure Applications (edge connectivity) §Robustness of supercomputers to failures of wires/fiber optics §Reliability of road networks with road closures/accidents §Communication networks’ resistance to link failure Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 2

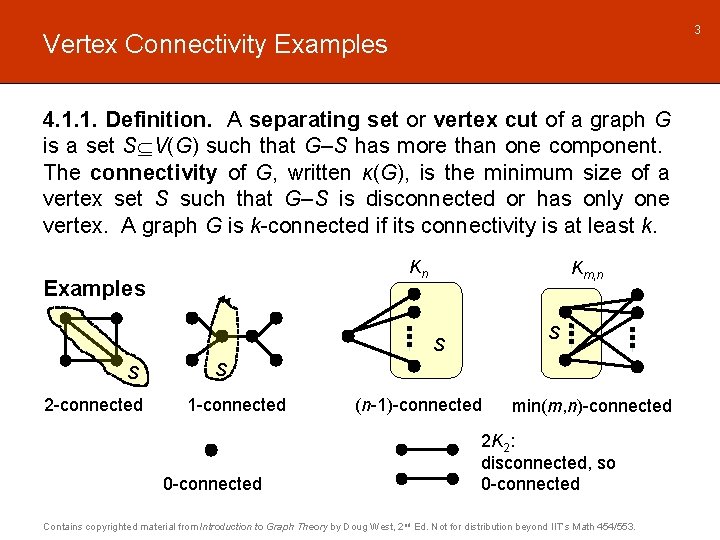
3 Vertex Connectivity Examples 4. 1. 1. Definition. A separating set or vertex cut of a graph G is a set S V(G) such that G–S has more than one component. The connectivity of G, written κ(G), is the minimum size of a vertex set S such that G–S is disconnected or has only one vertex. A graph G is k-connected if its connectivity is at least k. Kn Examples Km, n S S S 2 -connected S 1 -connected 0 -connected (n-1)-connected min(m, n)-connected 2 K 2: disconnected, so 0 -connected Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553.

4 Vertex Connectivity Examples 4. 1. 1. Definition. A separating set or vertex cut of a graph G is a set S V(G) such that G–S has more than one component. The connectivity of G, written κ(G), is the minimum size of a vertex set S such that G–S is disconnected or has only one vertex. A graph G is k-connected if its connectivity is at least k. K 1 K 2 K 3 K 4 Kn (n>3) C 4 Cn (n>2) Connectivity κ 0 1 2 3 n-1 2 2 1 -connected? N Y Y Y 2 -connected? N N Y Y Y 3 -connected? N N N Y Y N N Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553.

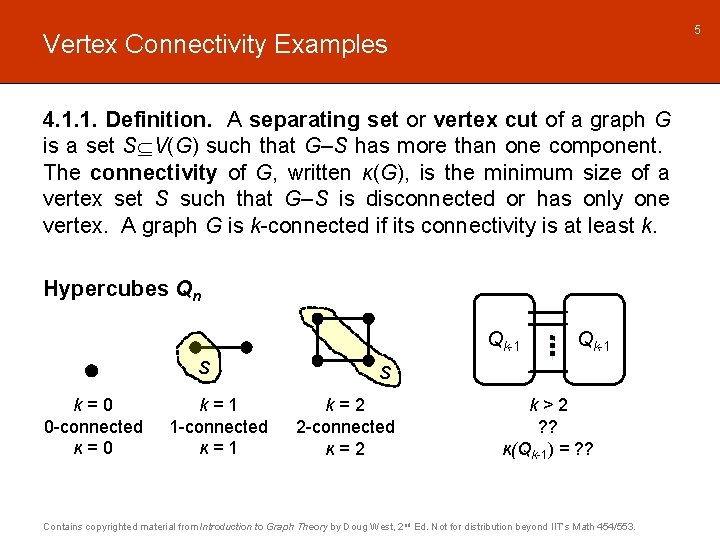
5 Vertex Connectivity Examples 4. 1. 1. Definition. A separating set or vertex cut of a graph G is a set S V(G) such that G–S has more than one component. The connectivity of G, written κ(G), is the minimum size of a vertex set S such that G–S is disconnected or has only one vertex. A graph G is k-connected if its connectivity is at least k. Hypercubes Qn Qk-1 S k=0 0 -connected κ=0 k=1 1 -connected κ=1 Qk-1 S k=2 2 -connected κ=2 k>2 ? ? κ(Qk-1) = ? ? Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553.

Vertex-Connectivity of the Hypercube 4. 1. 3. Example. The hypercube Qk has connectivity κ(Qk)=k for all k≥ 0. Proof (By induction on k. ) Base cases k=0, 1 have κ(Qk)=k by examples on previous slide. Induction step Let k≥ 2 and assume true for smaller k. The neighborhood of any v is a vertex cut, so κ(Qk) k. Qk-1 Q’k-1 View Qk as two copies of Qk-1 plus a perfect matching M. Suppose S is a vertex cut for Qk. Assume Qk–S leaves ≥ 1 vertex in Qk-1 and Q’k'-1, else |S| ≥ 2 k-1 ≥ k. Case 1 Both Qk-1–S and Q’k-1–S are connected: Unless S contains at least one endpoint of each edge of M, there is an edge between Qk-1–S and Q’k-1–S, making Qk–S connected. Therefore |S| ≥ |M| =2 k-1 ≥ k (since k ≥ 2). Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 6

Vertex-Connectivity of the Hypercube 4. 1. 3. Example. The hypercube Qk has connectivity κ(Qk)=k for all k≥ 0. Proof (By induction on k. ) View Qk as two copies of Qk-1 plus a perfect matching M. Qk-1 Q’k-1 Suppose S is a vertex cut for Qk. Assume Qk–S leaves ≥ 1 vertex in Qk-1 and Q’k'-1, else |S| ≥ 2 k-1 ≥ k. Case 2 At least one of Qk-1–S and Q’k-1–S is disconnected, say Qk-1–S: By induction, |S Qk-1| ≥ k-1. If |S Q’k-1| = 0, then Qk–S contains all of Q’k-1 and is thus connected. Therefore |S Q’k-1| ≥ 1, and so |S| ≥ k. Combining the lower bound of k on the size of a vertex cut with the observation that removal of the size k neighborhood of a vertex disconnects Qk, we have κ(Qk)=k for all k≥ 0. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 7

Vertex-Connectivity of the Hypercube Question Does there exist a vertex cut of size k in the k-dimensional hypercube that cannot be expressed as the neighborhood of a single vertex? This is a basic question in the area of isoperimetric problems in graphs. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 8

Minimum Size of a k-Connected Graph 4. 1. 5. Theorem (Harary [1962 a]) κ(Hk, n)=k, and hence the minimum number of edges in a k-connected graph on n vertices is kn/2. Proof outline. If a graph G has fewer than kn/2 edges, then δ(G)<k, and we can remove the neighbors of a vertex of minimum degree to demonstrate that G has connectivity less than k. The lower bound of kn/2 is sharp: §We proved the result for even k and 2 k<n using the Harary graph Hk, n §The result for odd k using the Harary graph Hk, n is similar. Two remarks: 1. We always have κ(G)<n. 2. When k=1, the bound is sharp when n=2 when G is K 2. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 9

Minimum Disconnecting Sets are Edge Cuts 4. 1. 7 Definition. A disconnecting set of edges is a set F E(G) such that G–F has more than one component. A graph is k-edgeconnected if every disconnecting set has at least k edges. The edgeconnectivity of G, written κ’(G), is the minimum size of a disconnecting set (equivalently, the maximum k such that G is k-connected). Given S, T V(G), we write [S, T] for the set of edges having one endpoint in S and the other in T. An edge cut is an edge set of the form [S, V(G)–S] where S is a nonempty proper subset of V(G). 4. 1. 8. Remark. §Every edge cut is a disconnecting set. §Every minimal disconnecting set is an edge cut: For a disconnecting set F, let H be a component of G–F. Then [V(H), V(G)–V(H)] is an edge cut. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 10

Connectivity and Min Degree for Simple Graphs 4. 1. 9 Theorem. (Whitney [1932 a]) If G is a simple graph, then κ(G) κ’(G) δ(G). Proof of κ’(G) δ(G): The edges incident to a vertex of minimum degree are a disconnecting set. Proof of κ(G) κ’(G): Let F be a minimum disconnecting set of G of size κ’(G), which is therefore equal to an edge cut [S, V(G)–S] by Remark 4. 1. 8. Case 1 Every vertex of S is adjacent to every vertex of V(G)–S. Then κ’(G) = |[S, V(G)–S]| n– 1, and n– 1 κ(G) we already knew. Case 2 There exist vertices x S and y V(G)–S with xy E(G). Define T= ( N(x) (V(G)–S) ) {z S–{x} : N(x) (V(G)–S) }. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 11

Connectivity and Min Degree for Simple Graphs 4. 1. 9 Theorem. (Whitney [1932 a]) If G is a simple graph, then κ(G) κ’(G) δ(G). Proof of κ(G) κ’(G): Case 2 There exist vertices x S and y V(G)–S with xy E(G). Define T = ( N(x) (V(G)–S) ) {z S–{x} : N(x) (V(G)–S) }. §T is a vertex cut because all x, y-paths would G would have to cross through T. x §The edges FT both incident to T and in the edge T cut [S, V(G)–S] are a disconnecting set. T T §Every vertex of T has at least one neighbor, so T |[S, V(G)–S] | |FT| |T|. T We have found a vertex cut T with size at most y the size of a minimum edge cut [S, V(G)–S], S V(G)–S and therefore κ(G) κ’(G). (|T| bold edges) Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 12

Arbitrary Space in Whitney’s Inequalities 4. 1. 10. Whitney’s inequalities κ(G) κ’(G) δ(G) can be made arbitrarily, and simultaneously, weak. The following graph has κ(G) = 1, κ’(G) = 2, δ(G) = 3 F S Important note: A 1 -vertex graph has κ’(G) = , so n(G)=1 is excluded. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 13

Connectivity in 3 -Regular Graphs 4. 1. 11 Theorem If G is a 3 -regular graph, then κ(G) = κ’(G). Important note: The graph G = is excluded from Thm. 4. 1. 11. (3 parallel edges between two vertices) There is no 3 -regular 1 -vertex graph, so we do know all 3 -regular graphs satisfy κ(G) κ’(G) δ(G) = 3. First, n(G) > 1 since no 1 -vertex graph is 3 -regular. There are two cases for a minimum vertex cut S. Case 1 n(G–S) = 1: Then G has the complete graph Kn as a spanning subgraph. This is only possible if n=2 and G = , or if n=4 and G = K 4, which has κ(G) = κ’(G) = 3. We prove Theorem 4. 1. 11 by assuming n(G–S) > 1. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 14

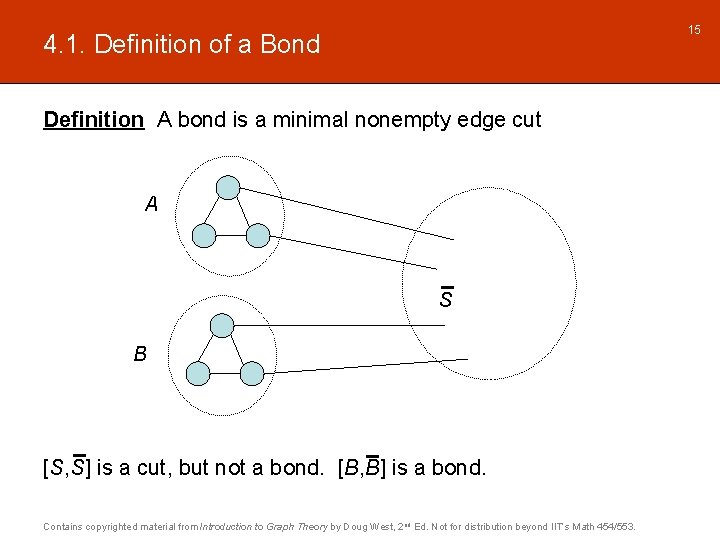
15 4. 1. Definition of a Bond Definition A bond is a minimal nonempty edge cut A S B [S, S] is a cut, but not a bond. [B, B] is a bond. Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553.

4. 1. Definition of a Block Defn A block H of a graph G is a maximal subgraph of G with no cut vertex. Properties of blocks of a simple graph G; distinct blocks H, H 1, H 2 (1) H is an isolated vertex, a cut-edge, or a maximal 2 connected subgraph (2) H 1 cannot be properly contained in H 2. (3) H 1Å H 2= , or H 1Å H 2={v}, v a cut-vertex (4) The blocks decompose G Contains copyrighted material from Introduction to Graph Theory by Doug West, 2 nd Ed. Not for distribution beyond IIT’s Math 454/553. 16