4 1 Congruent Polygons Naming Comparing Polygons List

4. 1 Congruent Polygons

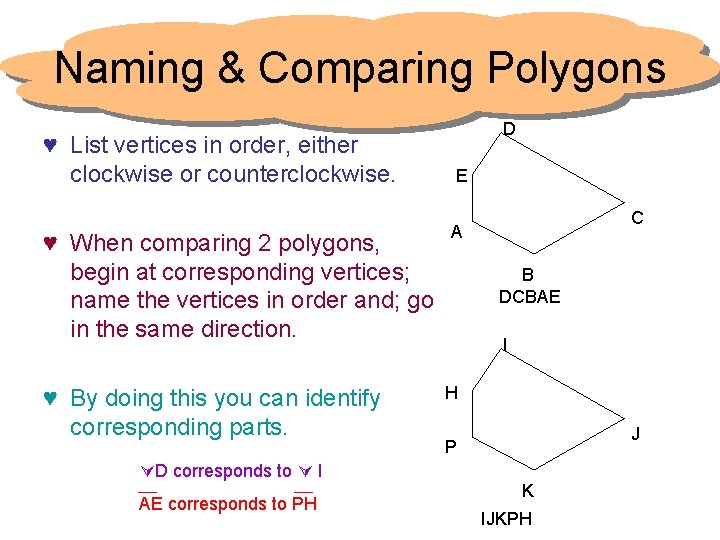
Naming & Comparing Polygons ♥ List vertices in order, either clockwise or counterclockwise. ♥ When comparing 2 polygons, begin at corresponding vertices; name the vertices in order and; go in the same direction. ♥ By doing this you can identify corresponding parts. D corresponds to I AE corresponds to PH D E C A B DCBAE I H J P K IJKPH

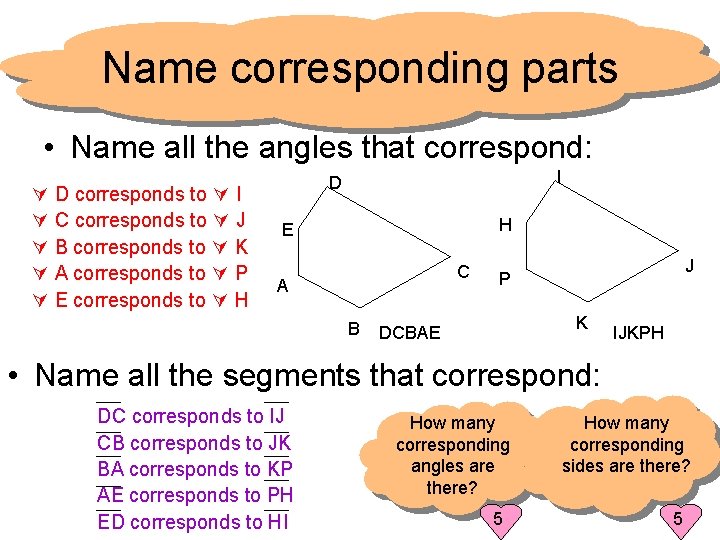
Name corresponding parts • Name all the angles that correspond: D corresponds to I C corresponds to J B corresponds to K A corresponds to P E corresponds to H I D H E C A B J P K DCBAE IJKPH • Name all the segments that correspond: DC corresponds to IJ CB corresponds to JK BA corresponds to KP AE corresponds to PH ED corresponds to HI How many corresponding angles are there? 5 How many corresponding sides are there? 5

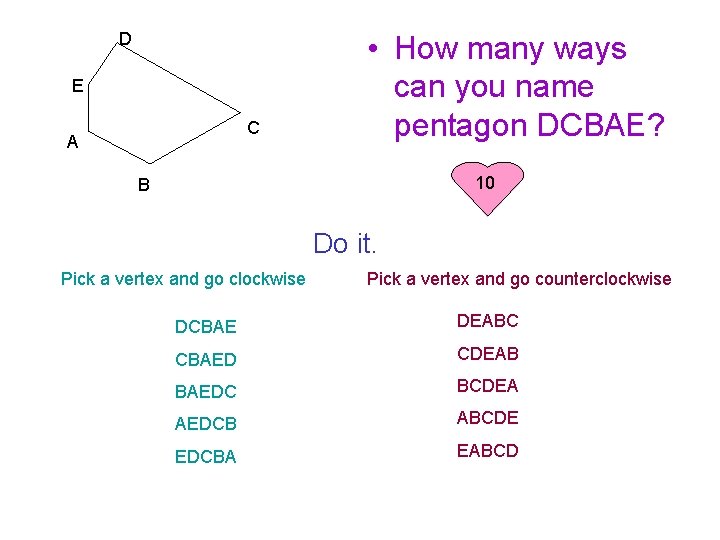
D E C A • How many ways can you name pentagon DCBAE? 10 B Do it. Pick a vertex and go clockwise Pick a vertex and go counterclockwise DCBAE DEABC CBAED CDEAB BAEDC BCDEA AEDCB ABCDE EDCBA EABCD

Polygon Congruence Postulate • If each pair of corresponding angles is congruent, and each pair of corresponding sides is congruent, then the two polygons are congruent.

Congruence Statements A • Given: These polygons are congruent. B CO • Remember, if they are congruent, they are EXACTLY the same. RU NG D E CE EN C TEM STA H T EN G ABCD ~ = EFGH F • That means that all of the corresponding angles are congruent and all of the corresponding sides are congruent. • DO NOT say that ‘all the sides are congruent” and “all the angles are congruent”, because they are not.

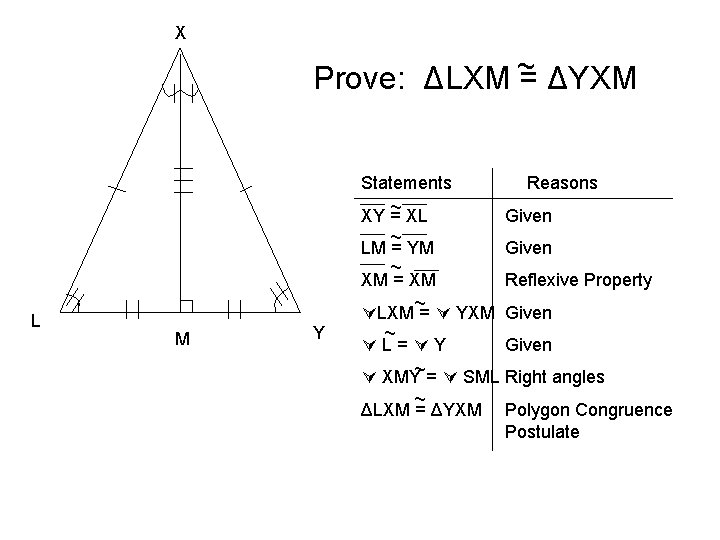
X Prove: ΔLXM ~ = ΔYXM Statements ~ XL XY = L M Y ~ LM = YM ~ XM = XM ~ LXM = YXM ~ L= Y XMY~= SML ~ ΔLXM = ΔYXM Reasons Given Reflexive Property Given Right angles Polygon Congruence Postulate

Assignment Pg 214; 10 -36 not 30 -34