4 1 15 Unit 10 Area Surface Area

4 -1 -15 Unit 10 Area, Surface Area, and Volume Prisms 1

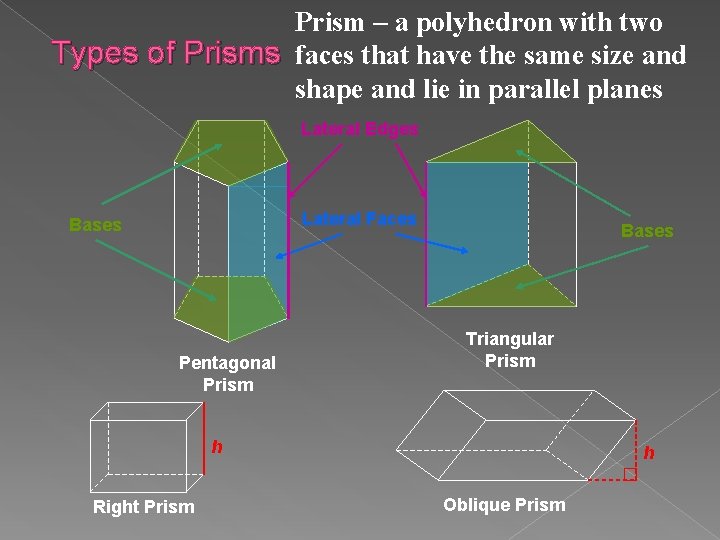
Vocabulary Polyhedron – a three-dimensional figure in which each surface is shaped like a polygon Face – a flat surface that is shaped like a polygon Edge – the segment formed by the intersection of two faces Vertex – a point at which three or more edges intersect Prism – a polyhedron with two faces that have the same size and shape and lie in parallel planes Base – the two faces on a prism that are parallel to each other Cylinder – is not a prism because it has two circles as bases Pyramid – is not a prism because it does not have two bases Lateral face – the faces that are not the bases, they are shaped like a parallelogram. Right – all lateral faces are rectangles that lie in planes perpendicular to the bases. Oblique – figures that are not right, they are slanted like they are getting pushed over.

Three-dimensional figures, or solids, are made up of flat surfaces. Each flat surface is called a face. A BASE is the face that are two repeating shapes. An edge is the segment that is the intersection of two faces.

Prism – a polyhedron with two Types of Prisms faces that have the same size and shape and lie in parallel planes Lateral Edges Lateral Faces Bases Pentagonal Prism Bases Triangular Prism h Right Prism h Oblique Prism

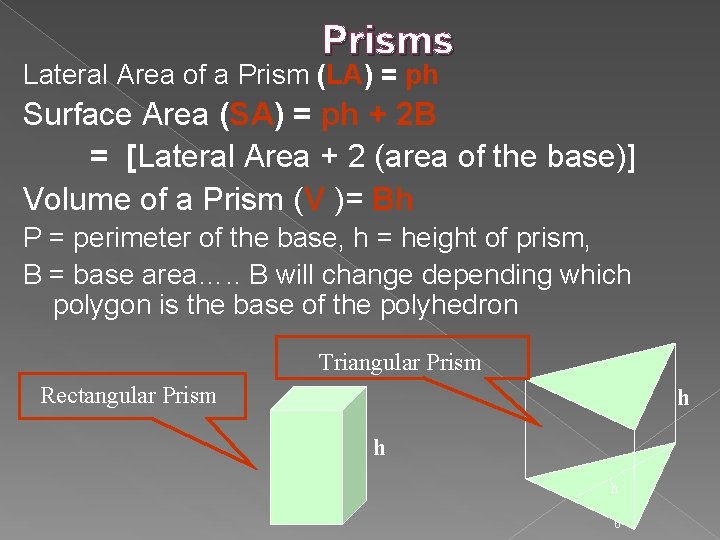
Prisms Lateral Area of a Prism (LA) = ph Surface Area (SA) = ph + 2 B = [Lateral Area + 2 (area of the base)] Volume of a Prism (V )= Bh P = perimeter of the base, h = height of prism, B = base area…. . B will change depending which polygon is the base of the polyhedron Triangular Prism Rectangular Prism h h h 6

Examples: h = 8 8 B = 5 x 4 = 20 5 4 perimeter of base = 2(5) + 2(4) = 18 L. A. = 18 x 8 = 144 sq. units S. A. = 144 + 2(20) = 184 sq. units V = 20 x 8 = 160 cubic units 7

Examples: 4 h = 4 B = ½ (6)(4) = 12 8 4 5 6 perimeter of base = 6 + 5 + 8 = 19 L. A. = 19 x 4 = 76 sq. units S. A. = 76 + 2(12) = 100 sq. units V = 12 x 4 = 48 cubic units 8

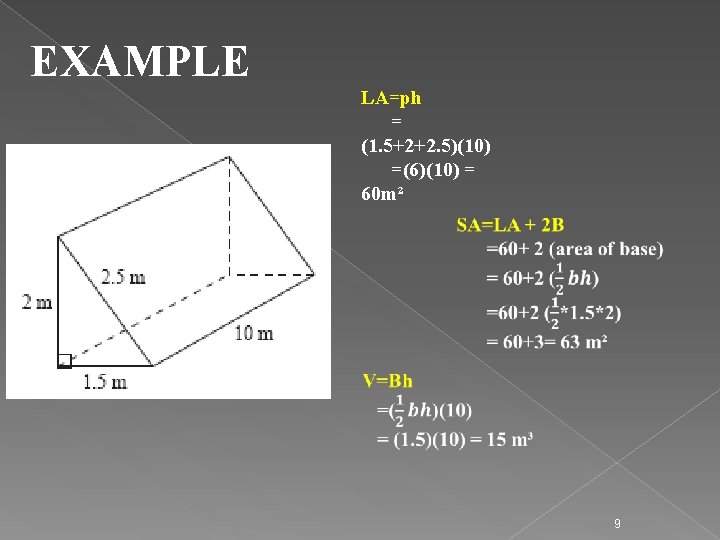
EXAMPLE LA=ph = (1. 5+2+2. 5)(10) =(6)(10) = 60 m² 9

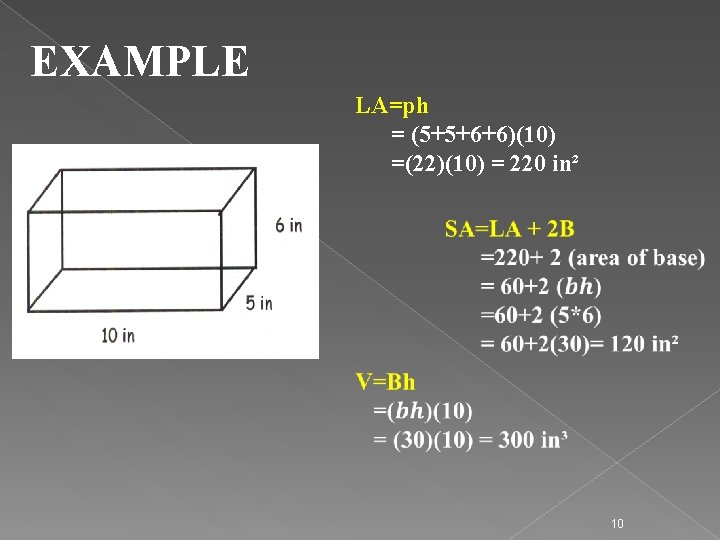
EXAMPLE LA=ph = (5+5+6+6)(10) =(22)(10) = 220 in² 10

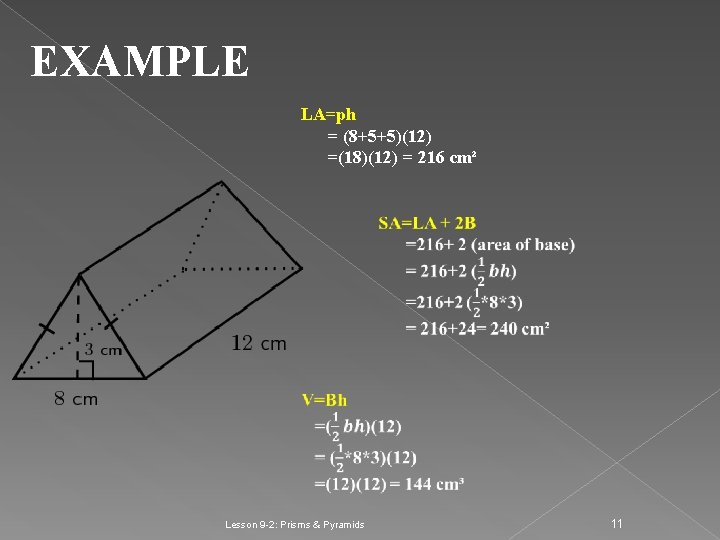
EXAMPLE LA=ph = (8+5+5)(12) =(18)(12) = 216 cm² Lesson 9 -2: Prisms & Pyramids 11

Example 3: Find the surface area and volume of the triangular prism. S. A. = ph + 2 B V = Bh 10 cm 5 cm 7 cm 4 cm

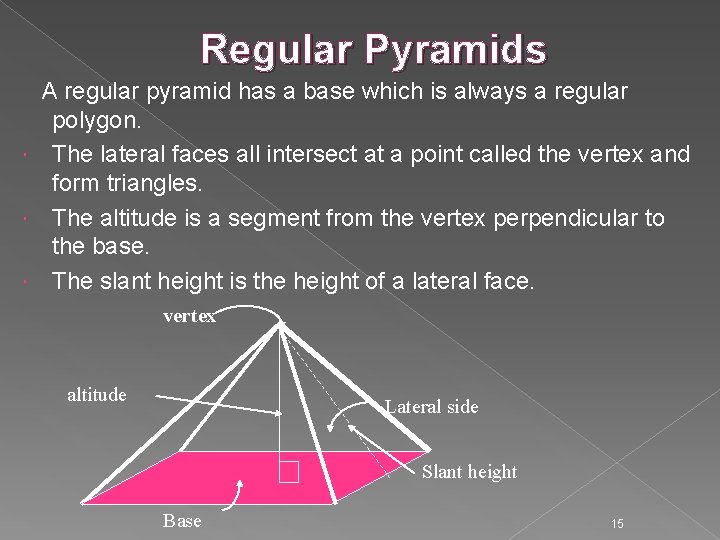
Regular Pyramids A regular pyramid has a base which is always a regular polygon. The lateral faces all intersect at a point called the vertex and form triangles. The altitude is a segment from the vertex perpendicular to the base. The slant height is the height of a lateral face. vertex altitude Lateral side Slant height Base 15

Regular Pyramid The lateral area of a regular pyramid (L. A. )= ½ lp Surface area of a regular pyramid (S. A. ) = ½ lp + B The volume of a right pyramid (V)= ⅓ Bh ( p = perimeter of the base, l = slant height, B = base area) Example: Perimeter = (2 x 10) + (2 x 10) = 40 13 12 Slant height l = 13 ; Height h = 12 Lateral area = ½ (13)(40) = 260 sq. units Area of base = 10 x 10 = 100 sq. units Surface area = 260 + 100 = 360 sq. units 10 10 Volume = ⅓ (100)(12) = 400 cubic units 16

Prism and Pyramids Formulas Prisms: › Lateral Area: L. A. = ph (p = perimeter, h = height) › Surface Area: S. A. = ph + 2 B (B = area of base) › Volume: V = Bh Regular Pyramids: › Lateral Area: L. A. = ½ lp (p = perimeter, l = slant height) › Surface Area: S. A. = ½ lp + B (B = area of base) › Volume: V = ⅓ Bh ( B = area of base, h = height) 18