39 Polynomial Functions and Graphs Objective Students will

3/9 Polynomial Functions and Graphs Objective: Students will be able to determine the characteristics of a polynomial function. Essential Question: If your smile was represented by a polynomial function, what are the characteristics of that function?

Higher Degree Polynomial Functions and Graphs Polynomial Function A polynomial function of degree n in the variable x is a function defined by where each ai is real, an 0, and n is a whole number. ¡ ¡ ¡ an is called the leading coefficient n is the degree of the polynomial a 0 is called the constant term
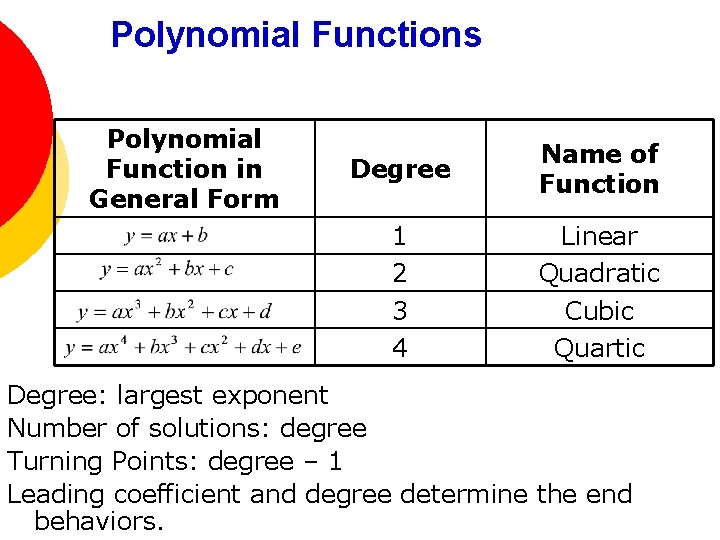
Polynomial Functions Polynomial Function in General Form Degree Name of Function 1 2 3 4 Linear Quadratic Cubic Quartic Degree: largest exponent Number of solutions: degree Turning Points: degree – 1 Leading coefficient and degree determine the end behaviors.
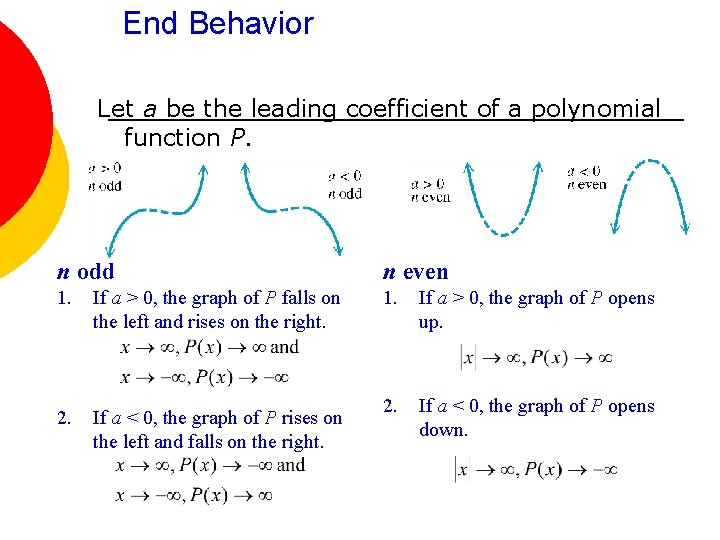
End Behavior Let a be the leading coefficient of a polynomial function P. n odd n even 1. If a > 0, the graph of P falls on the left and rises on the right. 1. If a > 0, the graph of P opens up. 2. If a < 0, the graph of P rises on the left and falls on the right. 2. If a < 0, the graph of P opens down.
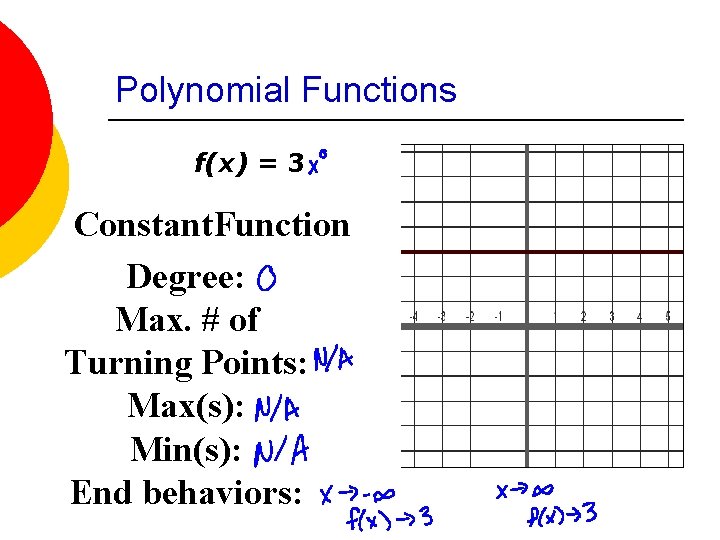
Polynomial Functions f(x) = 3 Constant. Function Degree: Max. # of Turning Points: Max(s): Min(s): End behaviors:
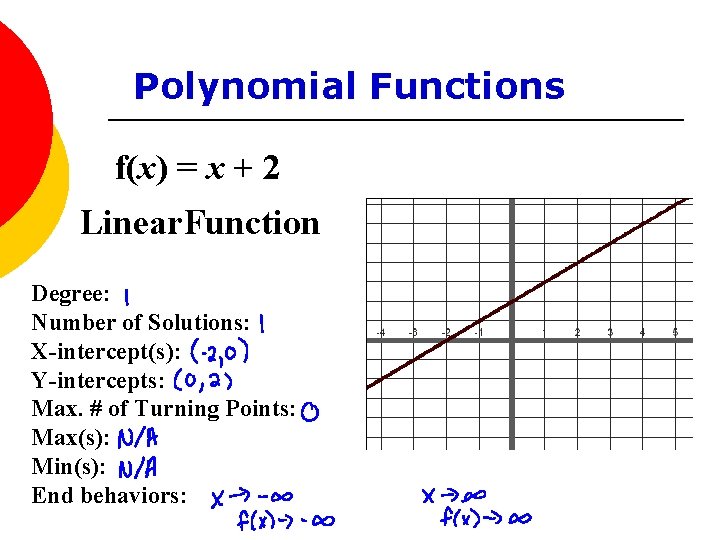
Polynomial Functions f(x) = x + 2 Linear. Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:
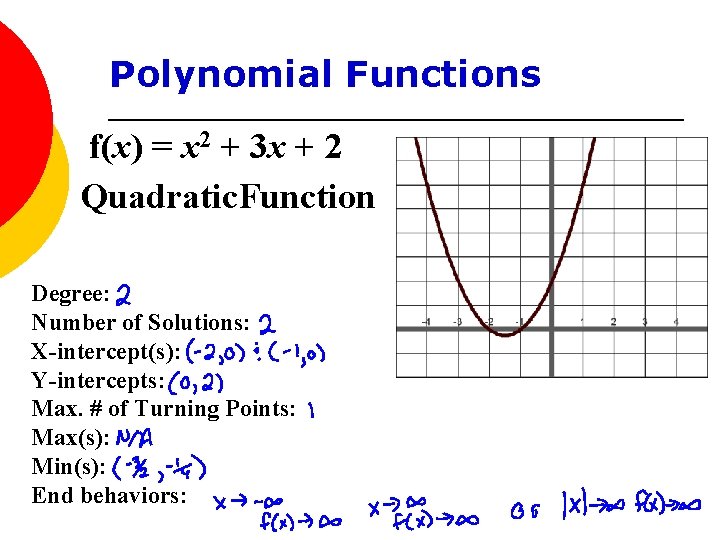
Polynomial Functions f(x) = x 2 + 3 x + 2 Quadratic. Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:
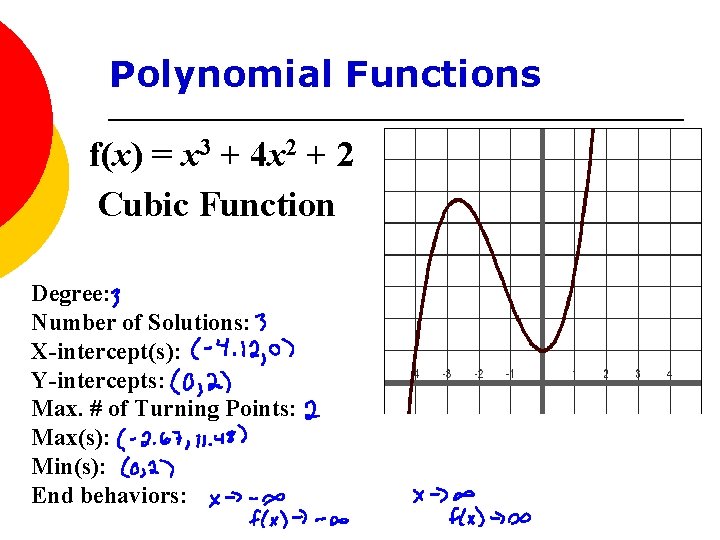
Polynomial Functions f(x) = x 3 + 4 x 2 + 2 Cubic Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:

Polynomial Functions f(x) = -x 3 + 2 x 2 – x – 2 Cubic Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:
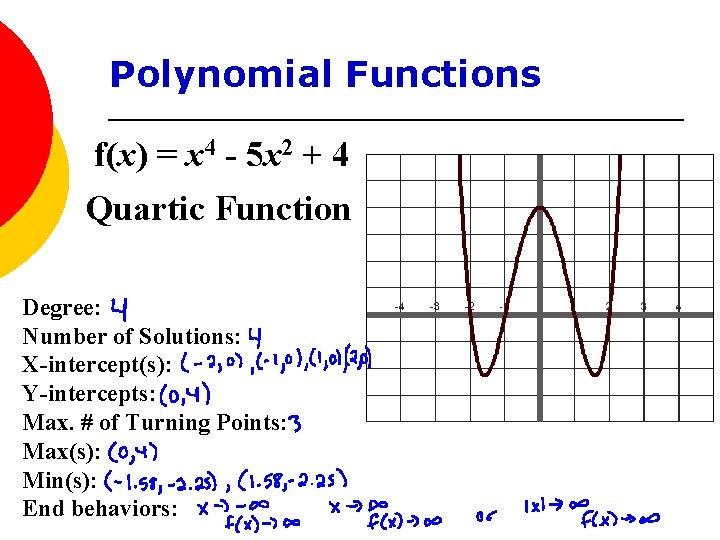
Polynomial Functions f(x) = x 4 - 5 x 2 + 4 Quartic Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:

Polynomial Functions f(x) = -2 x 4 + 8 x 3 – 8 x 2 + 2 Quartic Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:

Polynomial Functions f(x) = Quintic Function Degree: Number of Solutions: X-intercept(s): Y-intercepts: Max. # of Turning Points: Max(s): Min(s): End behaviors:
- Slides: 12