366 5 Sampling Defined The idea Making inference

366 5

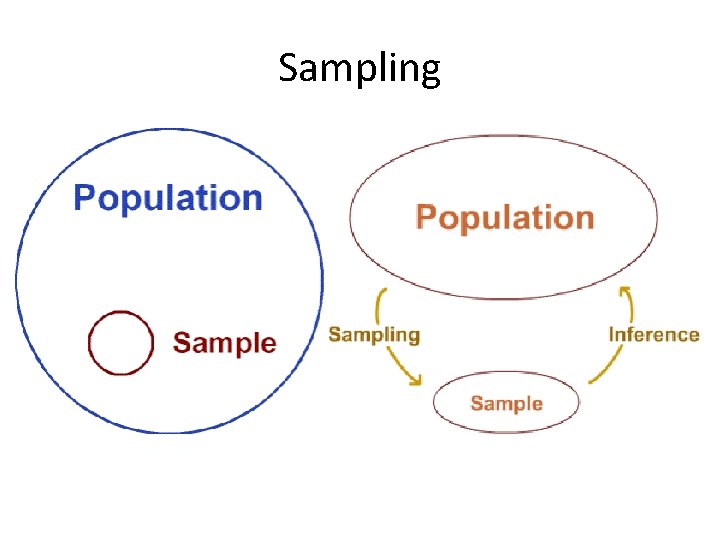
Sampling • Defined / The idea – Making inference about a larger population • What is the population – Some particular value in the population • estimating a parameter

Sampling

Sampling • Population must be defined – If interested in opinions of. . . • • All adults Registered voters Likely voters Actual voters • These are all distinct populations

Sampling • Population must be defined – If interested in opinions of. . . • • • People in Whatcom County Voters in Whatcom County People in Bellingham Voters in Bellingham Likely voters in Bellingham • These are all distinct populations

Sampling • Population must be defined – If interested in opinions of. . . • • Students at WWU Seniors at WWU (xxx # of credits & up) Students in College of Arts & Sciences etc. • These are all distinct populations; who should be included, excluded

Sampling • Sampling unit – A single member of the population • a case – If population = conflicts (wars) • sampling unit = nations of a certain size

Sampling • Sampling Frame • Once clear about what population & units are, how do we find them? – Frame = complete list of population • Registered voters; Students at WWU – In reality this may not exist • e. g. , all people living in the US

Sampling • Sampling Frame • US Census – How get ‘the list? ’ – $3 billion; 500, 000 workers. . .

Sampling • Sampling Frame • Registered voters; Students at WWU – Piece of cake? – Accuracy of sample depends on comprehensiveness of frame

Sampling • Sampling Frame • Ahead of time, evaluate for problems – Missing elements • New residents, newly registered voters, ? – Clusters • Census tracts, city blocks, Zip code, Area code, prefix – Take random draw of clusters, then random draw of households in cluster

Sampling • Sampling Frame • Ahead of time, evaluate for problems – Blank elements • Phone directories (address w/o #) • Phone #s (unassigned prefixes; fax machine; pager) • List of all residents when population = voters

Classic Sample Failure • 1936 Literary Digest Survey – Survey of 2. 4 million Americans – Predicted Alf Landon 57%, FDR 43% – Actual result FDR 62%, Landon 38% – Frame = 10 million people • subscribers to Digest; phone directories; club memberships

Classic Sample Failure • 1936 Literary Digest Survey – What went wrong?

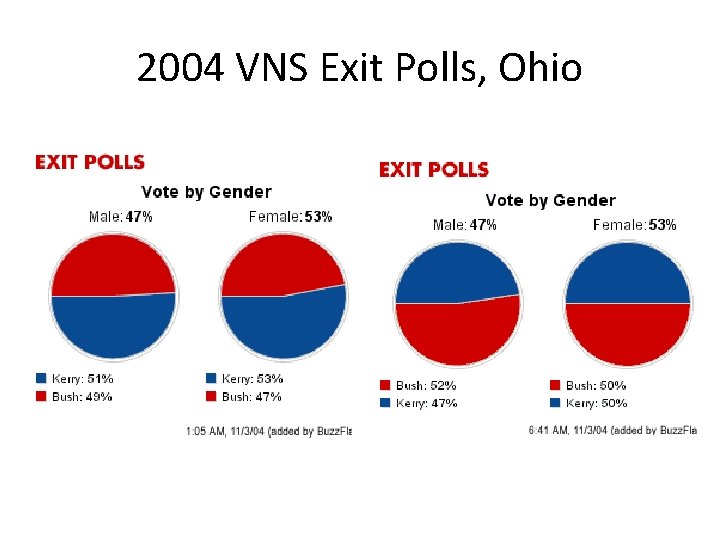
Classic Sample Failure • 2000 & 2004 & 2012 (WI) US Exit polls – Surveys of tens of thousands – 2000 initially predicted Gore win FL • Actually, Bush won – 2004 initially predicted Kerry win OH • Actually, Bush won • Frame: – Key precincts, people voting at polling places

2004 VNS Exit Polls, Ohio

“This can’t happen in America. Maybe in Ohio. . . ”

• http: //www. youtube. co m/watch? v=Ar. C 7 Xarwn WI • 2008 • http: //www. youtube. co m/watch? v=Io. WJkrlpt. N s

Classic Sample Failure • 2000 & 2004 US Exit polls – What went (goes) wrong? – also response bias that favors Democrats

Sample Designs • Probability vs. Non probability sampling – Probability sample • We know the probability that each unit in the population has of being in the sample – Non probability sample • We don’t know if every unit has a fixed chance of being in sample

Sample Design • Probability sample – If 22% of population are white, males over 21 years of age. . . – a. 22 probability that a white, male over 21 would end up in sample

Sample Design • Probability sample – If study repeated w/ different samples, high likelihood that results similar – We can estimate likelihood that things observed in the sample are representative of the population

Sample Design • Real world probability sample problems – Population = likely voters – Good sample frame? • Voters yes, likely voters no – Proper randomization • You try it – Missing elements • Land line vs. cell phones

Probability Samples • • Simple random sampling Systematic samples Stratified samples Cluster samples

Probability Samples • Simple random sampling – List each unit (person) in population – Give each a number (List from 1 to n) – Use random # generator – If 1207 comes up, select #1207 from list – Repeat

Probability Samples • Systematic sample – Have list of population, 1 – nth – Find random #, start there on list – Pick each kth unit (person) on list – Hope there is no structure to list • Starting point random, increment random – Easier • Kind of how exit polls work at polling place

Probability Sample • Stratified sample – Use available information from the population – Dived so elements w/ in groups (strata) are more alike than population – A series of homogeneous groups • Race/ethnicity; income – Combine samples into one • Cheaper

Probability Samples • Cluster sample – Identify clusters (groups) – Select large groups by random • Cities, congressional districts, states, neighborhoods – Randomly sample within cluster – Cheaper, no list of national US voters; consider face to face interviews

Probability Samples • • Simple random sampling Systematic samples Stratified samples Cluster samples • Other types, some of these used together

Non-probability Samples • Convenience sample – All students in this class • Population = WWU students – First 200 people walking down Railroad Ave. • Population = Whatcom County voters – No way to know representativeness of sample

Non-probability samples • Purposive sample – Units selected subjectively – Chance of being selected depends on researcher’s judgment – “Critical elections” • Population = all US Presidential elections – “Major wars” • Population = all wars

Non-probability sample • Quota sample – Purposively select sample as representative as possible – Use know characteristics of population – Target quota based on know characteristics

Non-probability sample • Quota sample – WWU (Fake example) • • 57% female, 43% male 45% A&S; 25% CST; 10% CBE; 10% Huxley; 10% other Age Ethnicity

Non-probability sample • Quota sample – Whatcom Co. (Fake example) • • Gender Age Partisanship City resident vs. County resident • Monitor demographics of respondents as you go

Non-probability sample • Quota sample – Poor person’s random sampling – Can fail to predict – 1948 3 surveys predicted Dewey to win – None targeted partisanship

Internet Samples • Opt-in • Provide people computers • Huge samples asked to do interviews • “Weight” data after responses to represent population

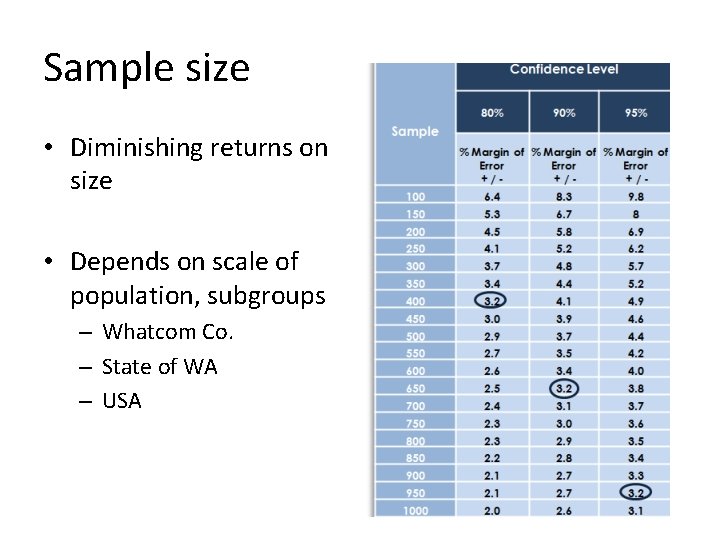
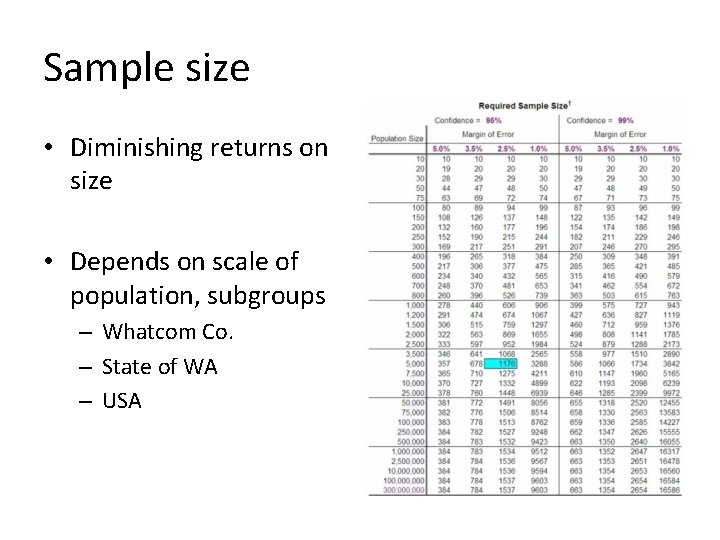
Sample size • If sample random (ish), precision of estimates depend on size • Larger = more precise estimate, all else equal • Very large doesn’t add much precision

Sample size • Diminishing returns on size • Depends on scale of population, subgroups – Whatcom Co. – State of WA – USA

Sample size • Diminishing returns on size • Depends on scale of population, subgroups – Whatcom Co. – State of WA – USA