332 437 Lecture 13 FSM Asynchronous Inputs Clocks

332: 437 Lecture 13 FSM Asynchronous Inputs, Clocks, and Hazards n n n n 2/20/2021 Asynchronous inputs Clock distribution Counters State reduction Synchronizing Sequences Races and Hazards One-Hot Design Summary Bushnell: Digital Systems Design Lecture 13 1

Material from An Engineering Approach to Digital Design, by William I. Fletcher, Prentice-Hall Inc. 2/20/2021 Bushnell: Digital Systems Design Lecture 13 2

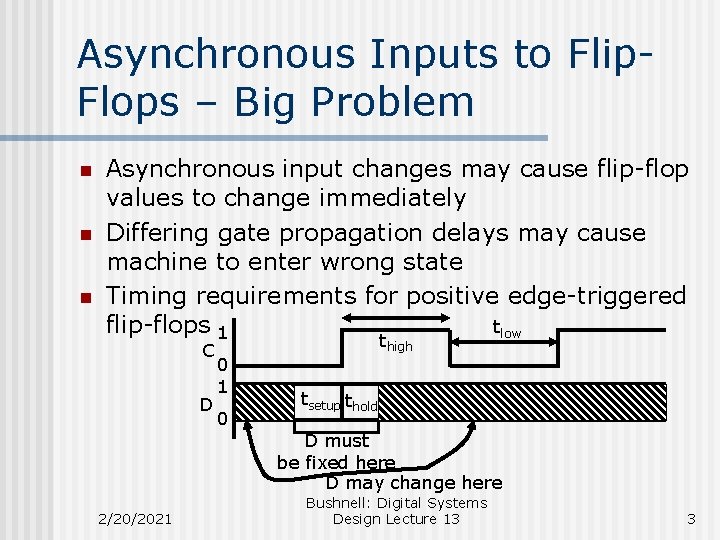
Asynchronous Inputs to Flip. Flops – Big Problem n n n Asynchronous input changes may cause flip-flop values to change immediately Differing gate propagation delays may cause machine to enter wrong state Timing requirements for positive edge-triggered flip-flops 1 tlow C D 0 1 0 thigh tsetup thold D must be fixed here D may change here 2/20/2021 Bushnell: Digital Systems Design Lecture 13 3

Runt Pulse n n Logic gate inputs – pulse must have minimum width to cause gate output to change Very short pulses do not cause output to change, but could cause a blip on gate output much later after a randomly-chosen Dt 1 1 0 2/20/2021 Bushnell: Digital Systems Design Lecture 13 4

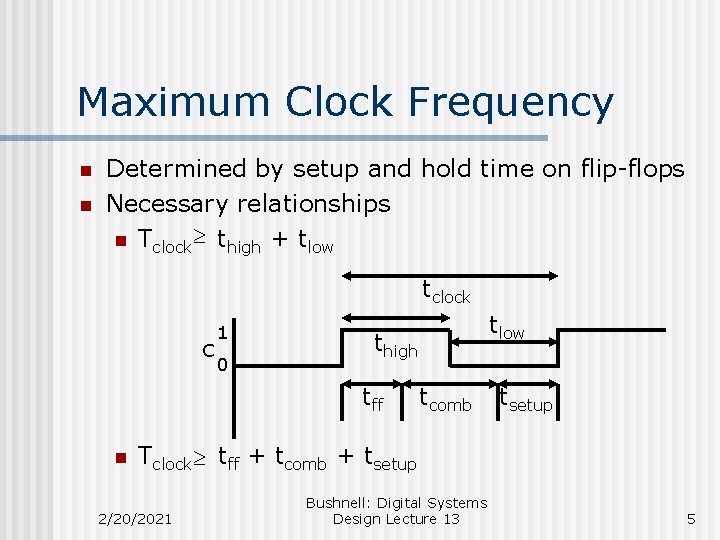
Maximum Clock Frequency n n Determined by setup and hold time on flip-flops Necessary relationships n Tclock ³ thigh + tlow tclock C 1 0 thigh tff n tlow tcomb tsetup Tclock ³ tff + tcomb + tsetup 2/20/2021 Bushnell: Digital Systems Design Lecture 13 5

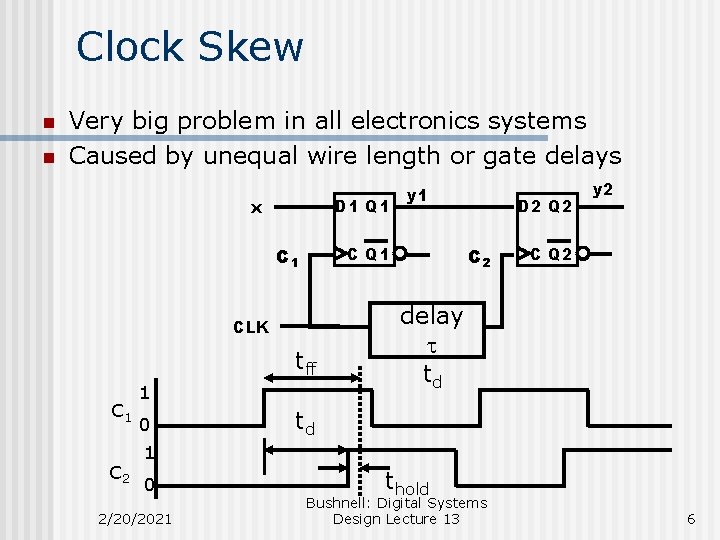
Clock Skew n n Very big problem in all electronics systems Caused by unequal wire length or gate delays D 1 Q 1 x C Q 1 CLK tff C 1 C 2 1 0 y 1 D 2 Q 2 C 2 y 2 C Q 2 delay t td td 1 0 2/20/2021 thold Bushnell: Digital Systems Design Lecture 13 6

New Clock Skew Constraints n n n td + thold £ tff (min) Minimum flip-flop delay So td £ tff (min) – thold Solutions: 1. Never Gate the Clock! Violated all the time by VLSI designers to save circuit power 2. Introduce matched delay l on clock line to C 1 3. Design clock wiring so that same wire length exists from clock source to all flipflops (H-tree)Bushnell: Digital Systems 2/20/2021 Design Lecture 13 7

Example H-Tree n Most of VLSI circuit signal propagation delay is caused by the wiring n Same distance from clock source to all X’s CLK Chip X X X X 2/20/2021 Bushnell: Digital Systems Design Lecture 13 8

Counters n n n n Repeat a state after some number, N, of clock pulses Mod N – remainder after dividing by N If counter in state n after m clock pulses, will be in state n after m + N, m + 2 N, … pulses States assigned as 0 to 2 N – 1 Binary Up Counter – sequence 0 to 2 N – 1 Binary down counter – reversed up counter sequence Decade up counter – 0, 1, 2, …, 10 n – 1, 0, 1, 2 2/20/2021 Bushnell: Digital Systems Design Lecture 13 9

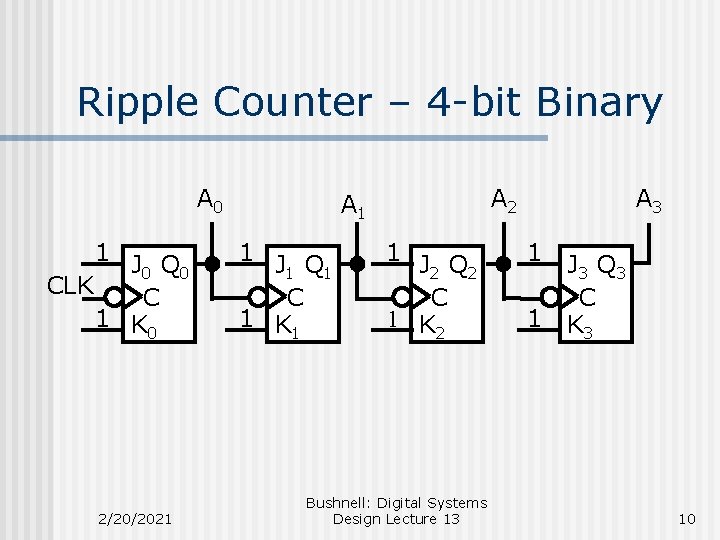
Ripple Counter – 4 -bit Binary A 0 1 J Q 0 0 CLK C 1 K 0 2/20/2021 A 2 A 1 1 J Q 1 1 C 1 K 1 1 J Q 2 2 C 1 K 2 Bushnell: Digital Systems Design Lecture 13 A 3 1 1 J 3 Q 3 C K 3 10

Counter Timing Behavior CLK A 0 0 1 0 1 0 0 1 t 1 0 0 1 1 0 A 2 0 0 1 1 1 0 A 3 0 0 0 0 1 t A 1 0 t 2/20/2021 Bushnell: Digital Systems Design Lecture 13 11

Counter Categories ripple (asynchronous) binary octal decimal special synchronous ripple carry parallel carry n To make a counter decimal: From count 1001 go to 0000 Right after we enter 1010 state Q 1 Q 3 up down up/down 000 Reset NOT USED because of gate races & unpredictable counting results • Considered to be a poor design 2/20/2021 Bushnell: Digital Systems Design Lecture 13 12

Up/Down Control n n Change direction: 1. Use Q side to drive next clock 2. Use Q signals as counter outputs 3. Change negative edge to positive edge flipflops Problems: 1. Very Slow 2. Varying gate & flip-flop delays can cause malfunctions 2/20/2021 Bushnell: Digital Systems Design Lecture 13 13

Better (More Reliable) Counters n 1. 2. 3. Synchronous All clocks connected in parallel Faster Operation Mode: Whenever all least significant bits are 1, next digit must change 0000 0001 0010 Use T flip-flops 0011 0100 … Bushnell: Digital Systems 2/20/2021 Design Lecture 13 14

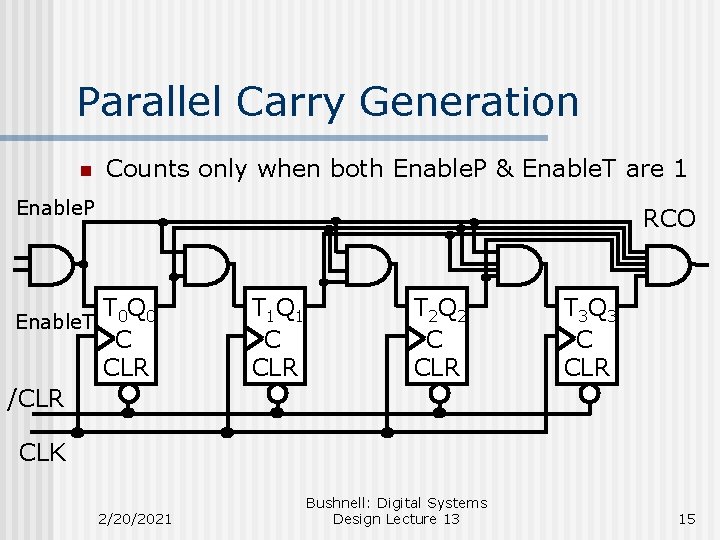
Parallel Carry Generation n Counts only when both Enable. P & Enable. T are 1 Enable. P RCO T 0 Q 0 Enable. T C CLR /CLR T 1 Q 1 C CLR T 2 Q 2 C CLR T 3 Q 3 C CLR CLK 2/20/2021 Bushnell: Digital Systems Design Lecture 13 15

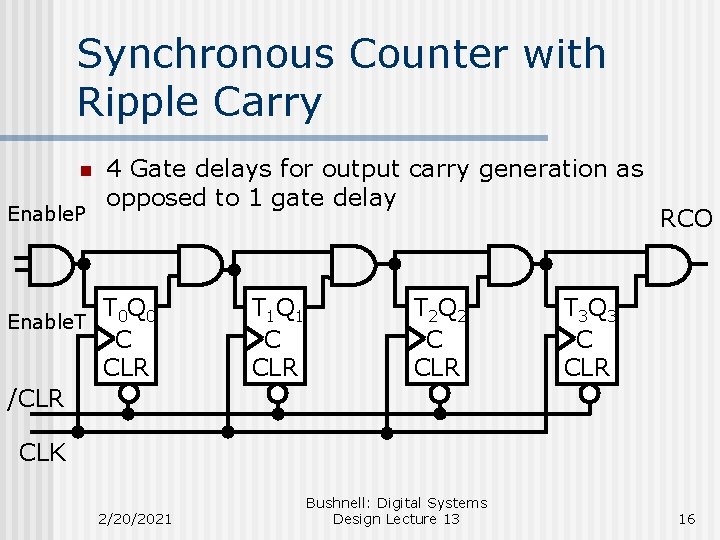
Synchronous Counter with Ripple Carry n Enable. P 4 Gate delays for output carry generation as opposed to 1 gate delay T 0 Q 0 Enable. T C CLR /CLR T 1 Q 1 C CLR T 2 Q 2 C CLR RCO T 3 Q 3 C CLR CLK 2/20/2021 Bushnell: Digital Systems Design Lecture 13 16

Shift Registers n n Types: 1. Serial-in, serial-out 2. Serial-in, parallel-out 3. Parallel-in, parallel-out 4. Bidirectional parallel-in, parallel-out Use a barrel shifter whenever possible: 1. Less hardware 2. Faster 2/20/2021 Bushnell: Digital Systems Design Lecture 13 17

Reduction of Finite State Machines n n Method: n Try all possible input sequences & note differences in output sequences • Note non-equivalent states x z Example Mealy machine: 0 1 1 0 A B 0 C 0 B D 0 B 0 C E 0 F 0 D E 0 F 0 E D 0 1 F C D/1 0 2/20/2021 Bushnell: Digital Systems Design Lecture 13 18

Problems of State Partitioning n n Cannot just look for identical rows in State Transition Table Frequently, the machine cycles between three or more states that are actually equivalent, but the rows in the State Transition Table for these 3 states do not look the same n Therefore, just looking for identical rows causes you to miss equivalent states 2/20/2021 Bushnell: Digital Systems Design Lecture 13 19

State Reduction by Method of Partitions n n n First partition – all states P 0: (ABCDEF) n Apply X = 0 – No difference in behavior n Apply X = 1 – If in F, output is 1, otherwise output is 0 • Leads to second partition P 1: (ABCDE) (F) n Apply X = 0 to ABCDE – no output difference n Apply X = 1 to ABCDE – If in ABC, stay in ABCDE partition, if in DE, go into another partition (F) • Leads to third partition 2/20/2021 Bushnell: Digital Systems Design Lecture 13 20

Method of Partitions (concluded) n n n P 2: (ABC) (DE) (F) n Apply X = 0 to ABC – If in A, stay in ABC, if in BC, go to DE • Leads to fourth partition P 3: (A) (BC) (DE) (F) n Apply X = 0 to BC – goes to DE n Apply X = 1 to BC – stays in BC n Apply X = 0 to DE – stays in DE n Apply X = 1 to DE – goes to F • No further partitioning possible Also works for Moore Machines 2/20/2021 Bushnell: Digital Systems Design Lecture 13 21

Synchronizing Sequences n n Input sequence that causes a Finite State Machine to be in a specified state, regardless of its initial state at the beginning of the sequence Example: X 0 1 A A B B C B B 2/20/2021 Bushnell: Digital Systems Design Lecture 13 22

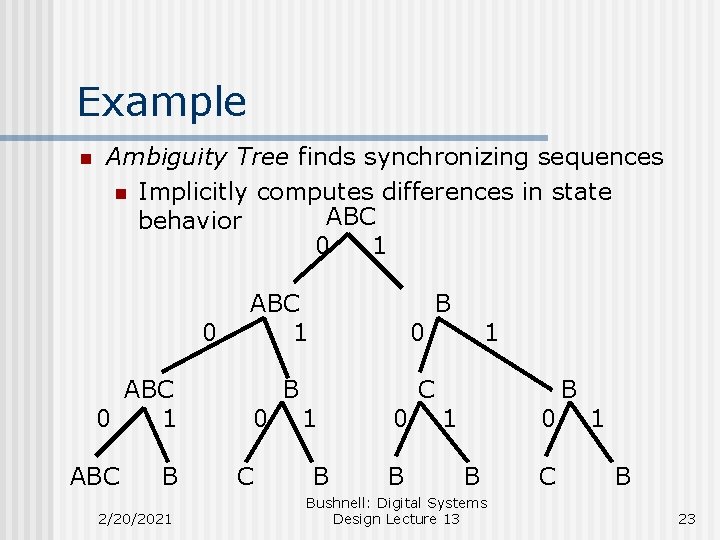
Example n Ambiguity Tree finds synchronizing sequences n Implicitly computes differences in state ABC behavior 0 1 0 ABC 0 1 ABC B 2/20/2021 ABC 1 0 C B 0 1 B 0 B C B 1 1 0 B Bushnell: Digital Systems Design Lecture 13 C B 1 B 23

Synchronizing Sequences n n Exist for B & C but not for A State Shortest Synchronizing Sequence B 1 C 10 Not all sequences are synchronizing sequences – e. g. , 00 If a Synchronizing Sequence Exists for State Si, then it exists for all States Sj reachable from state Si Strongly Connected Finite State Machine n All states reachable from every state 2/20/2021 Bushnell: Digital Systems Design Lecture 13 24

Search of Ambiguity Tree n n n Want to find SHORTEST synchronizing sequence for each state, so: n Search tree in a breadth-first manner Labels in tree are called the ambiguity – indicate the uncertainty about which state the machine is in Once you have explored the tree for a given ambiguity n If you encounter the same ambiguity again, you need not search it, as you will get the same answer you got last time you explored it 2/20/2021 Bushnell: Digital Systems Design Lecture 13 25

Synchronizing Sequences n n n If $ Synchronizing Sequence, then for a FSM to be strongly connected, we must have a synchronizing sequence for all states Must first reduce FSM to find the shortest synchronizing sequence Finite Memory Span: FSM has finite memory span of length K if: 1. All input sequences ³ K are synchronizing sequences 2. Each state can be reached by a synchronizing sequence of length £ K 2/20/2021 Bushnell: Digital Systems Design Lecture 13 26

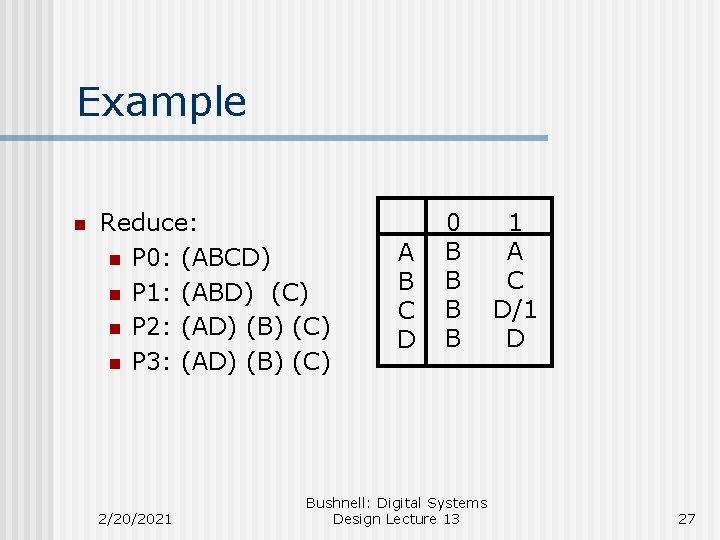
Example n Reduce: n P 0: (ABCD) n P 1: (ABD) (C) n P 2: (AD) (B) (C) n P 3: (AD) (B) (C) 2/20/2021 A B C D 0 B B Bushnell: Digital Systems Design Lecture 13 1 A C D/1 D 27

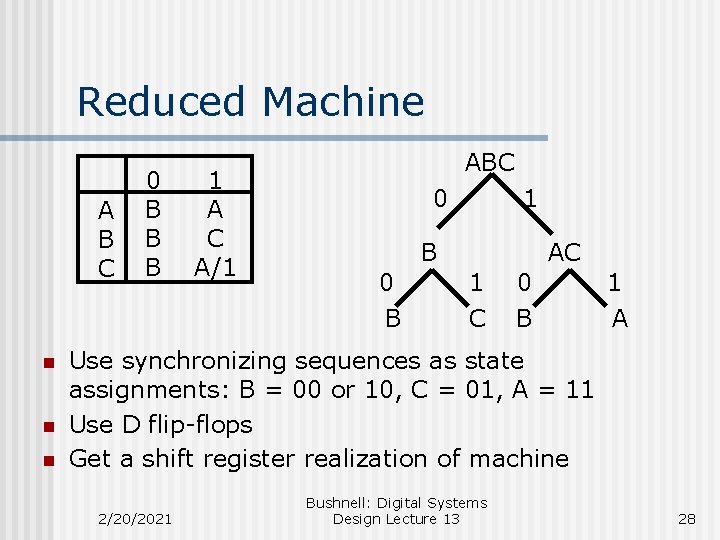
Reduced Machine A B C n n n 0 B B B 1 A C A/1 ABC 0 1 B 0 B AC 1 C 0 B 1 A Use synchronizing sequences as state assignments: B = 00 or 10, C = 01, A = 11 Use D flip-flops Get a shift register realization of machine 2/20/2021 Bushnell: Digital Systems Design Lecture 13 28

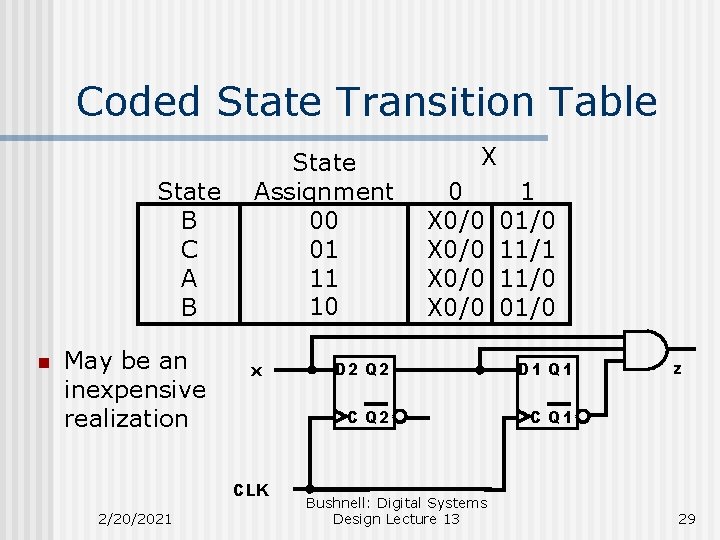
Coded State Transition Table State B C A B n May be an inexpensive realization State Assignment 00 01 11 10 x CLK 2/20/2021 X 0/0 X 0/0 1 01/0 11/1 11/0 01/0 D 2 Q 2 D 1 Q 1 C Q 2 C Q 1 Bushnell: Digital Systems Design Lecture 13 z 29

Races and Hazards n n Z-hazard – a glitch on a state machine output Race – change of more than one Flip-Flop required by State Transition Table n Example: going from state 10 to 01 Non-critical race – correct operation occurs no matter which Flip-Flop changes first Critical race – possible to make a mistake and end up in the wrong state when the wrong Flip. Flop changes first 2/20/2021 Bushnell: Digital Systems Design Lecture 13 30

Static and Dynamic Hazards n n n Static Hazard – Momentary transient in output signal that should have remained static in response to input change n Exists whenever there adjacent input combinations in K-Map with same output & no map sub–code covers both combinations n Generally, 1 0 transition causes hazard Dynamic Hazard – Multiple momentary transient in output signal that should have changed only once in response to input change Essential Hazard -- Operational error causing transition to improper state in response to input changes, caused by excessive delay on feedback variable in response to input change 2/20/2021 Bushnell: Digital Systems Design Lecture 13 31

Hazard Examples Static Dynamic Input Output 1. 2. 3. 4. Caused by circuit delays, which are randomly distributed during chip manufacturing Essential hazards exist only in sequential circuits with 2+ feedbacks Result from a combination of both delay & design specifications Can be controlled by adjusting the state assignment n Requires understanding of asynchronous circuit design Bushnell: Digital Systems 2/20/2021 Design Lecture 13 32

Static Hazards n n n Theorem: A static 0 (1) hazard exists if there is a pair of adjacent states with 0 (1) outputs and there is no 0 (1) set that covers both No static hazards in network if: 1. There is a 1 (0) set that covers every adjacent input state having an output of 1 (0) 2. There are no 1 (0) sets containing exactly 1 pair of complemented literals Essential Hazard – a property of the circuit input/output behavior 1. No way to eliminate it 2. There will be some combination of circuit delays will cause a glitch, no matter how you realize the circuit 2/20/2021 Bushnell: Digital Systems Design Lecture 13 33

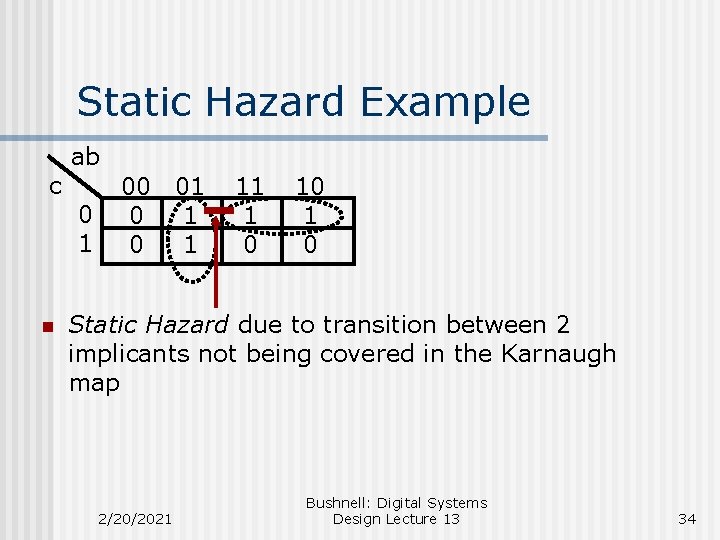
Static Hazard Example c n ab 0 1 00 01 0 1 11 1 0 10 1 0 Static Hazard due to transition between 2 implicants not being covered in the Karnaugh map 2/20/2021 Bushnell: Digital Systems Design Lecture 13 34

Static Hazard Example z 0 1 n n n xy 00 01 11 10 0 1 1 1 0 1 Hazard-free SOP realization n SOP is hazard-free, here, provided that we do not factor it Hazard in POS Tradeoff between simplicity of design and hazard -free operation 2/20/2021 Bushnell: Digital Systems Design Lecture 13 35

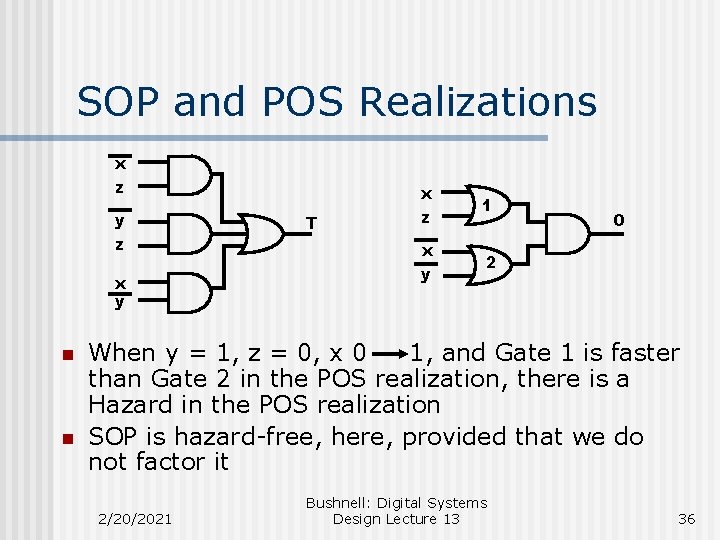
SOP and POS Realizations x z y z x y n n T x z x y 1 O 2 When y = 1, z = 0, x 0 1, and Gate 1 is faster than Gate 2 in the POS realization, there is a Hazard in the POS realization SOP is hazard-free, here, provided that we do not factor it 2/20/2021 Bushnell: Digital Systems Design Lecture 13 36

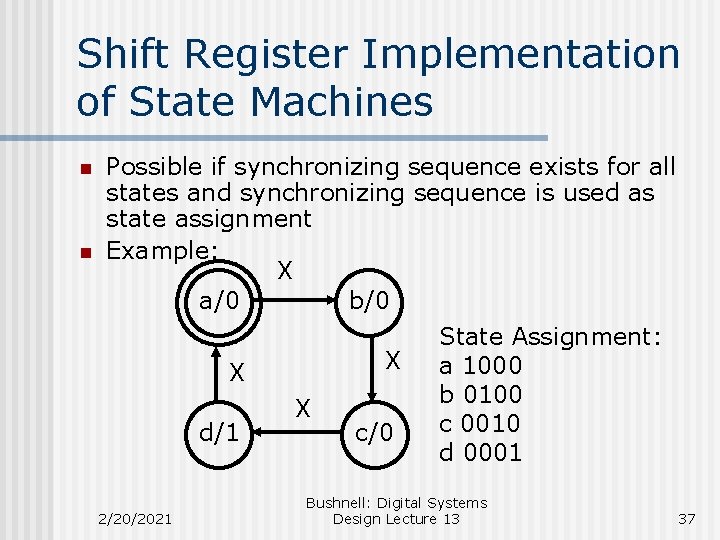
Shift Register Implementation of State Machines n n Possible if synchronizing sequence exists for all states and synchronizing sequence is used as state assignment Example: X a/0 b/0 State Assignment: X a 1000 X b 0100 X c 0010 d/1 c/0 d 0001 2/20/2021 Bushnell: Digital Systems Design Lecture 13 37

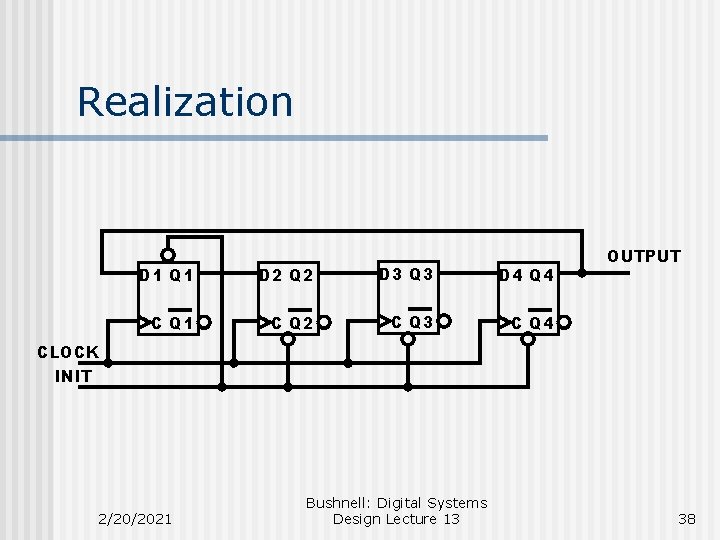
Realization D 1 Q 1 D 2 Q 2 D 3 Q 3 D 4 Q 4 C Q 1 C Q 2 C Q 3 C Q 4 OUTPUT CLOCK INIT 2/20/2021 Bushnell: Digital Systems Design Lecture 13 38

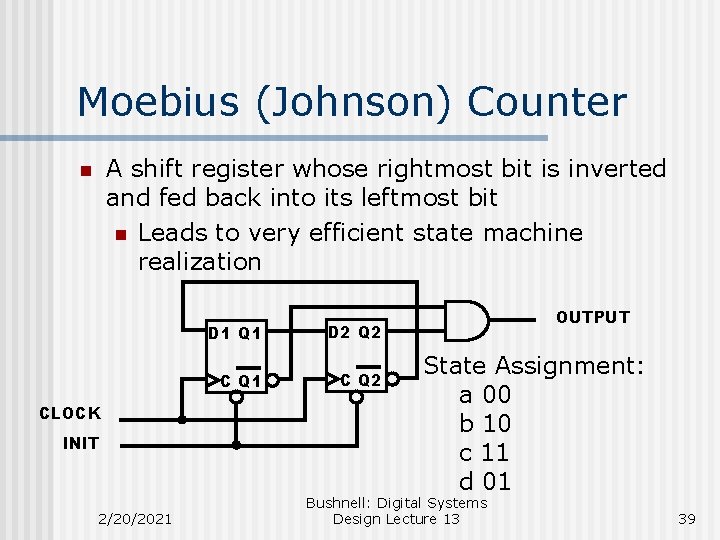
Moebius (Johnson) Counter A shift register whose rightmost bit is inverted and fed back into its leftmost bit n Leads to very efficient state machine realization n CLOCK INIT 2/20/2021 D 1 Q 1 D 2 Q 2 C Q 1 C Q 2 OUTPUT State Assignment: a 00 b 10 c 11 d 01 Bushnell: Digital Systems Design Lecture 13 39

One-Hot Design n n Use 1 D Flip-Flop (FF) for each state, only 1 D FF set to 1 at any given time Advantage: Look at appropriate D FF to see if the machine is in the corresponding state n Grossly simplifies output decoder Disadvantage: In a mprocessor, could lead to billions of FFs n Leads to huge amounts of hardware and an untestable machine Use this method ONLY for relatively simple machines 2/20/2021 Bushnell: Digital Systems Design Lecture 13 40

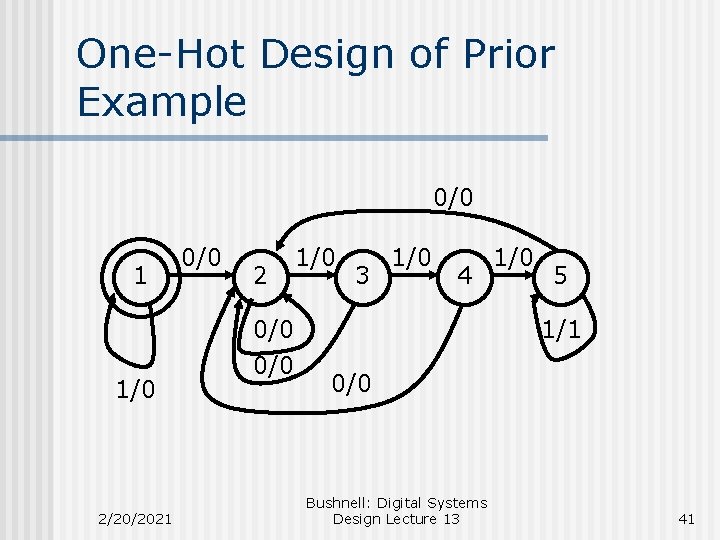
One-Hot Design of Prior Example 0/0 1 1/0 2/20/2021 0/0 2 0/0 1/0 3 1/0 4 1/0 5 1/1 0/0 Bushnell: Digital Systems Design Lecture 13 41

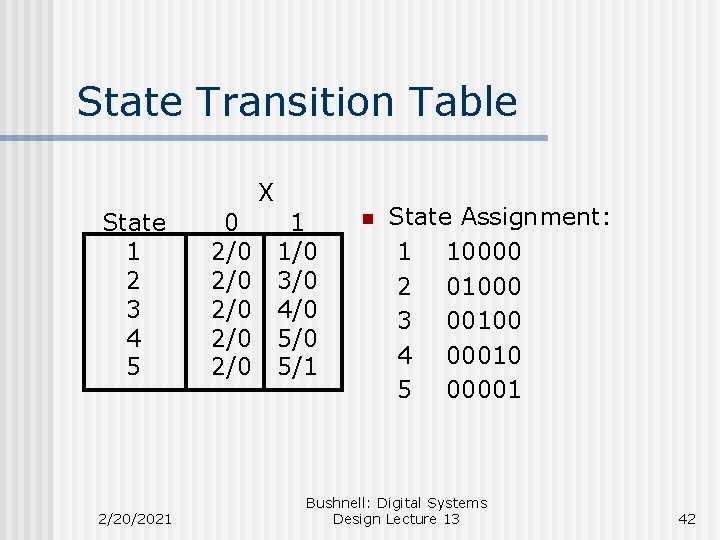
State Transition Table X State 1 2 3 4 5 2/20/2021 0 2/0 2/0 2/0 1 1/0 3/0 4/0 5/1 n State Assignment: 1 10000 2 01000 3 00100 4 00010 5 00001 Bushnell: Digital Systems Design Lecture 13 42

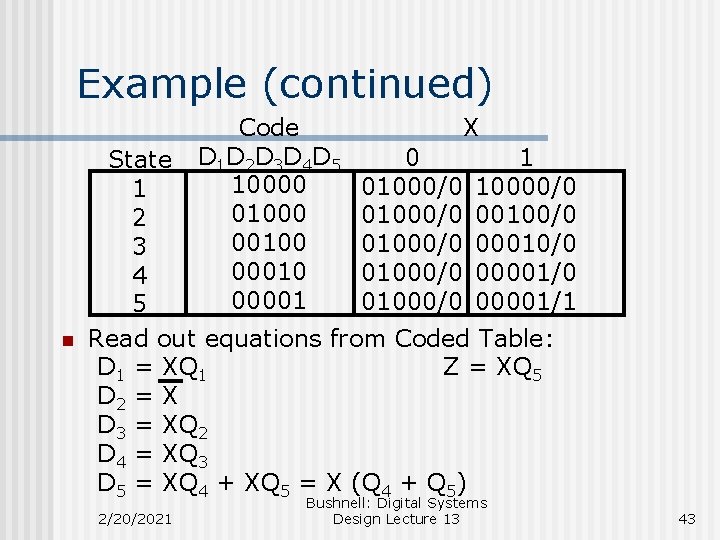
Example (continued) Code D 1 D 2 D 3 D 4 D 5 10000 01000 00100 00010 00001 n X 0 1 State 01000/0 10000/0 1 01000/0 00100/0 2 01000/0 00010/0 3 01000/0 00001/0 4 01000/0 00001/1 5 Read out equations from Coded Table: D 1 = XQ 1 Z = XQ 5 D 2 = X D 3 = XQ 2 D 4 = XQ 3 D 5 = XQ 4 + XQ 5 = X (Q 4 + Q 5) 2/20/2021 Bushnell: Digital Systems Design Lecture 13 43

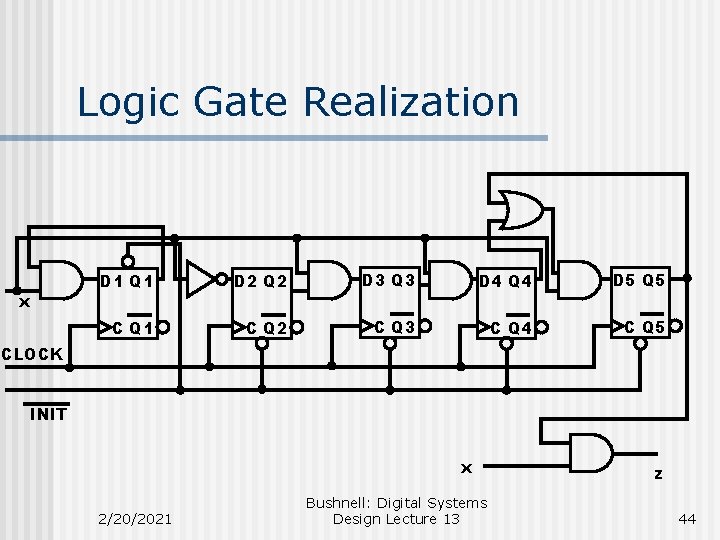
Logic Gate Realization x D 1 Q 1 D 2 Q 2 D 3 Q 3 D 4 Q 4 D 5 Q 5 C Q 1 C Q 2 C Q 3 C Q 4 C Q 5 CLOCK INIT x 2/20/2021 Bushnell: Digital Systems Design Lecture 13 z 44

Summary n n n n 2/20/2021 Asynchronous inputs Clock distribution Counters State reduction Synchronizing Sequences Races and Hazards One-Hot Design Bushnell: Digital Systems Design Lecture 13 45