30 years of chaos research from a personal

30 years of chaos research from a personal perspective Peter H. Richter 不来梅大学物理系 中国科学院 — 马普学会计算生物学伙伴研究所 CAS-MPG Partner Institute for Computational Biology 上海 2007 年 3 月 29 日 Shanghai, March 29, 2007 Peter H. Richter 1

Outline 1. 2. 3. 4. 5. 6. 7. 8. 9. History Dynamical systems: general perspective Deterministic chaos: regular vs. chaotic dynamics Example I: the Lorenz system Example II: the double pendulum Scenarios of transition to chaos: universality Chaos and fractals: dynamics and geometry Hamiltonian systems: entanglement of order and chaos Other developments and summary Peter H. Richter 2

1. History • • • • 1890 Poincaré: Méthodes nouvelles de la mécanique céleste 1925 Strömgren: numerical determination of periodic orbits 1963 Kolmogorov, Arnold, Moser: invariant irrational tori 1963 Lorenz: period doubling scenario and butterfly effect 1967 Smale: „horseshoes“ contain invariant Cantor sets 1970 Kadanoff, Wilson: renormalization – scaling, universality 1975 Mandelbrot: fractal geometry 1975 Aspen conference on network dynamics 1975 Li & Yorke: „period three implies chaos“ 1977 Großmann & Thomae: analysis of period doubling 1978 Feigenbaum: universality of period doubling 1978 Berry‘s review on regular and irregular motion 1981 Bremen conference on invariant sets in chaotic dynamics 1985 Exhibition „Frontiers of Chaos“ Peter H. Richter 3

2. Dynamical Systems: general perspective • systems „live“ in phase space – of low dimension, compact or open – or of high dimension (infinite in case of PDEs) • and develop in time – continuous time: differential equations – discrete time: difference equations • the dynamical laws may be – deterministic (no uncertainty in the laws) – stochastic (due to fluctuations) • the phase space flow may be – dissipative (contracting due to friction or other losses) – conservative (no friction, no expansion) – expansive (due to autocatalysis or other positive feedback) Peter H. Richter 4

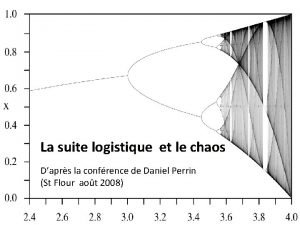
3. Deterministic chaos: regular vs. chaotic dynamics • dynamical point of view: long term (un)predictability – regular motion: points that lie initially close together tend to stay together or increase their distance at most linearly with time – chaos = sensitive dependence on initial conditions: points that lie initially close together get separated exponentially in time (Lyapunov exponents) • geometric point of view – regular motion: the phase space is „foliated“ by low-dimensional sets; given an initial condition, the possible future is strongly restricted – chaotic motion: given an initial condition, relatively large portions of phase space may be visited though not necessarily the entire space • symbolic point of view – regular motion generates regular sequences of numbers – chaotic motion generates random sequences of numbers Peter H. Richter 5

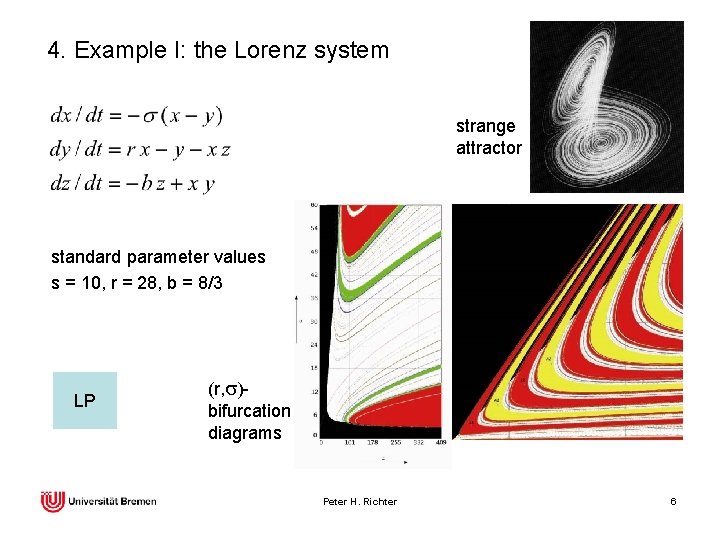
4. Example I: the Lorenz system strange attractor standard parameter values s = 10, r = 28, b = 8/3 LP (r, s)bifurcation diagrams Peter H. Richter 6

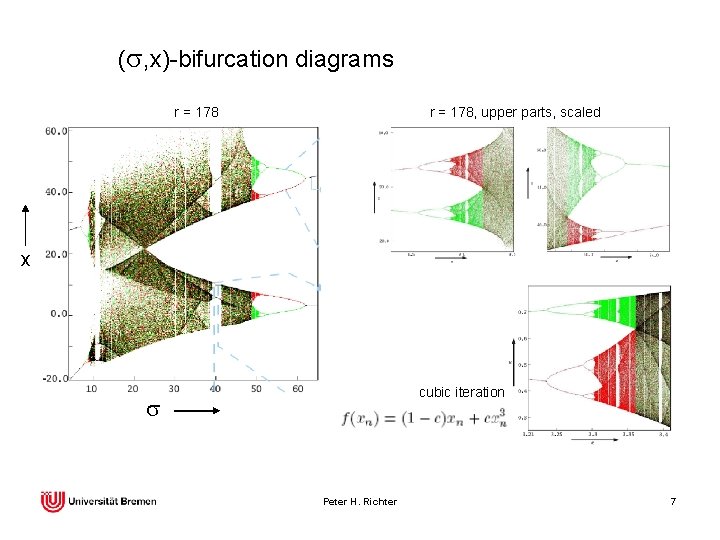
(s, x)-bifurcation diagrams r = 178, upper parts, scaled r = 178 x cubic iteration s Peter H. Richter 7

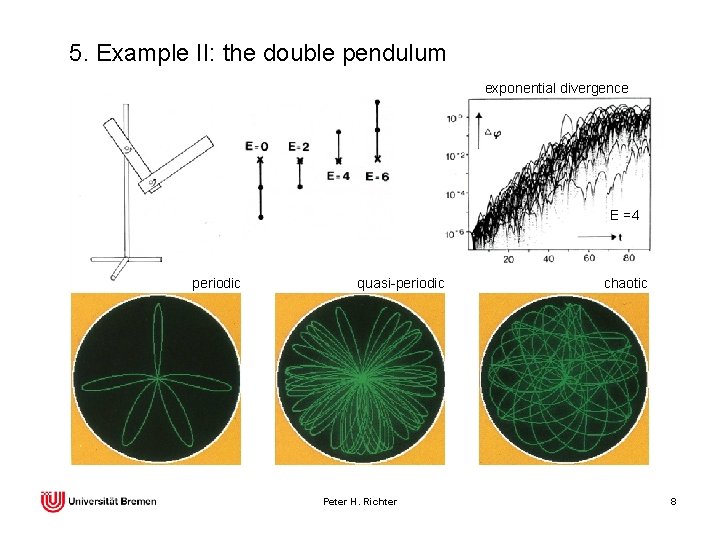
5. Example II: the double pendulum exponential divergence E =4 periodic quasi-periodic Peter H. Richter chaotic 8

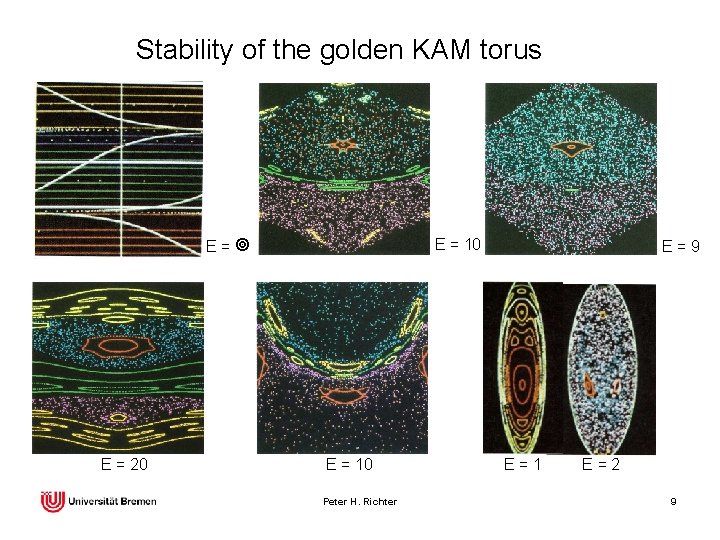
Stability of the golden KAM torus E = 10 E = 20 E = 10 Peter H. Richter E=9 E=1 E=2 9

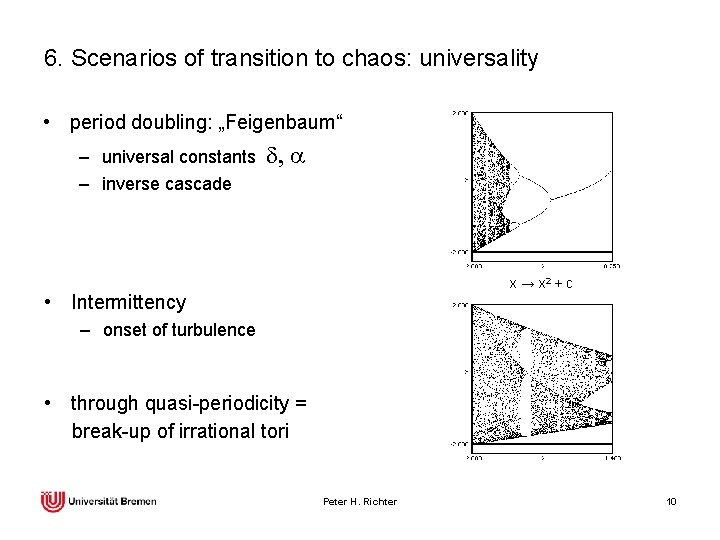
6. Scenarios of transition to chaos: universality • period doubling: „Feigenbaum“ – universal constants – inverse cascade d, a x → x 2 + c • Intermittency – onset of turbulence • through quasi-periodicity = break-up of irrational tori Peter H. Richter 10

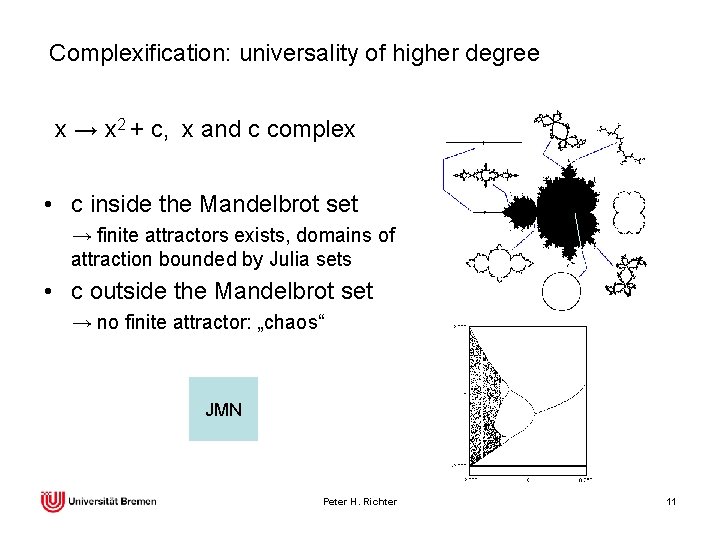
Complexification: universality of higher degree x → x 2 + c, x and c complex • c inside the Mandelbrot set → finite attractors exists, domains of attraction bounded by Julia sets • c outside the Mandelbrot set → no finite attractor: „chaos“ JMN Peter H. Richter 11

7. Chaos and fractals: dynamics and geometry • • • dissipative systems: chaotic (= strange) attractors have fractal dimensions meromorphic systems: chaotic repellors (= Julia sets) have fractal dimension Hamiltonian systems: chaotic regions are „fat fractals“ Peter H. Richter 12

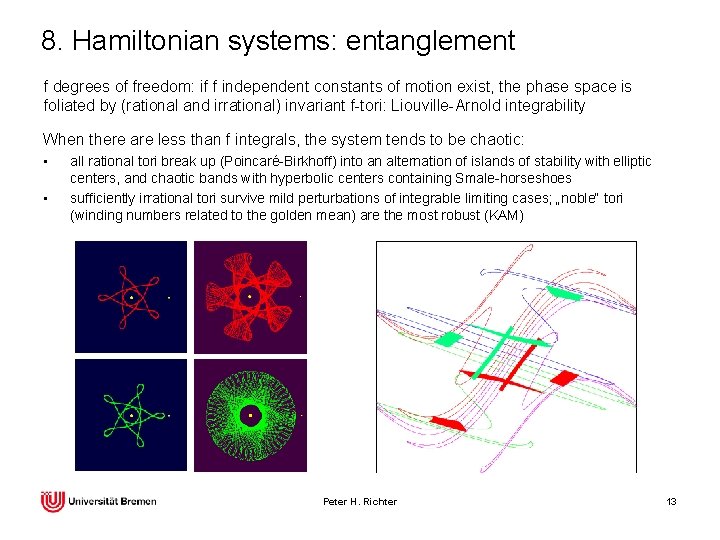
8. Hamiltonian systems: entanglement f degrees of freedom: if f independent constants of motion exist, the phase space is foliated by (rational and irrational) invariant f-tori: Liouville-Arnold integrability When there are less than f integrals, the system tends to be chaotic: • • all rational tori break up (Poincaré-Birkhoff) into an alternation of islands of stability with elliptic centers, and chaotic bands with hyperbolic centers containing Smale-horseshoes sufficiently irrational tori survive mild perturbations of integrable limiting cases; „noble“ tori (winding numbers related to the golden mean) are the most robust (KAM) Peter H. Richter 13

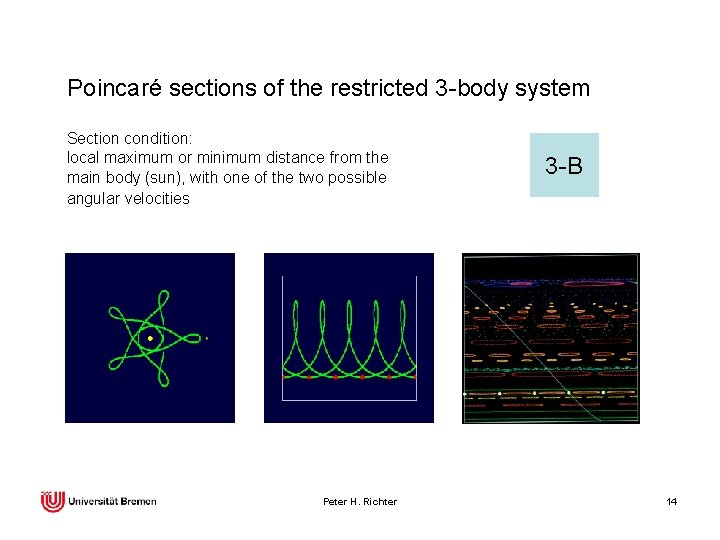
Poincaré sections of the restricted 3 -body system Section condition: local maximum or minimum distance from the main body (sun), with one of the two possible angular velocities Peter H. Richter 3 -B 14

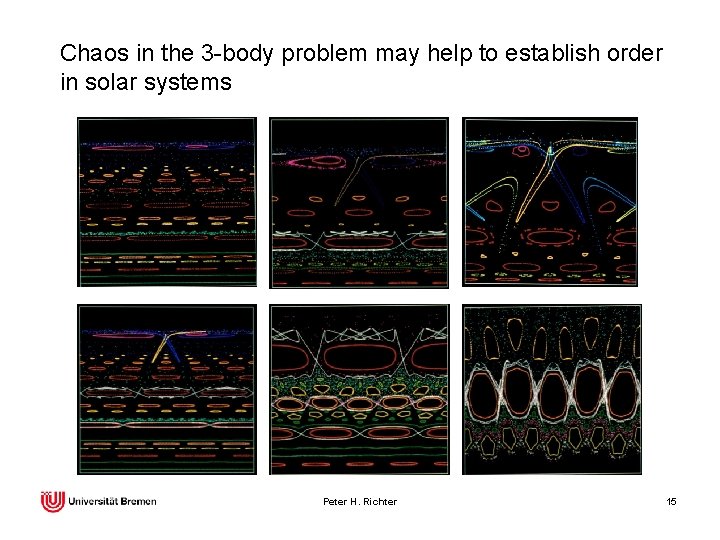
Chaos in the 3 -body problem may help to establish order in solar systems Peter H. Richter 15

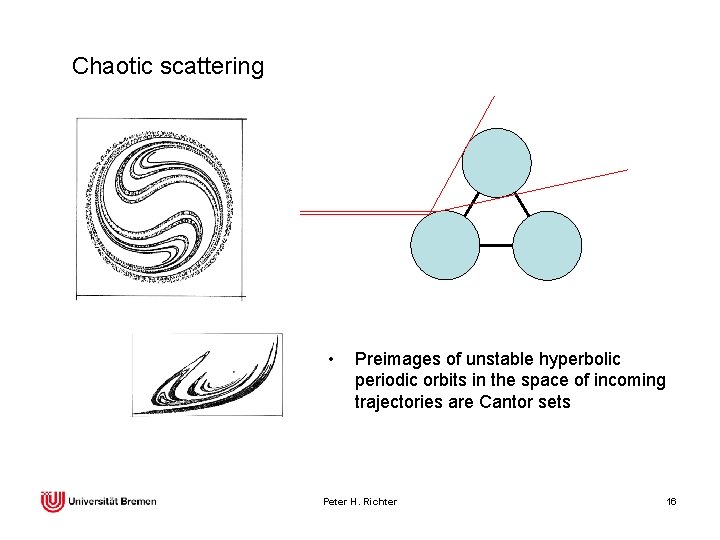
Chaotic scattering • Preimages of unstable hyperbolic periodic orbits in the space of incoming trajectories are Cantor sets Peter H. Richter 16

9. Other developments and summary • • • from celestial mechanics to molecular dynamics quantum chaos: level statistics, scars, quasi-classical quantization rigid body dynamics more than 2 degrees of freedom theory of turbulence (many degrees of freedom) influence of stochastic elements in the dynamics fractal growth patterns synchronization of non-linear oscillators neurodynamics econophysics …… Peter H. Richter 17

Summary • • • Chaos theory has deep roots in science. It emerged from questions on stability and predictability of systems, is founded on solid mathematical insight, but was boosted by the development of computer technology. The identification of universal scenarios came as an exciting surprise As chaos is the rule rather than the exception, there are many discoveries yet to be made 谢谢你们的兴趣 Peter H. Richter 18