30 Outline Maxwells Equations and the Displacement Current




![Energy and Momentum in EM Waves • Intensity: energy/area/time [watts/sq. meter] 9 Energy and Momentum in EM Waves • Intensity: energy/area/time [watts/sq. meter] 9](https://slidetodoc.com/presentation_image/dca33ada4e3ac191e108ceed2fc27ee5/image-9.jpg)






- Slides: 21

30 Outline • Maxwell’s Equations and the Displacement Current • Electromagnetic Waves • Polarization 1

displacement current • ‘explains’ existence of B around E 2

Maxwell’s Equations • Gauss’ Law: E & B • Faraday’s Law • Ampere’s Law 3

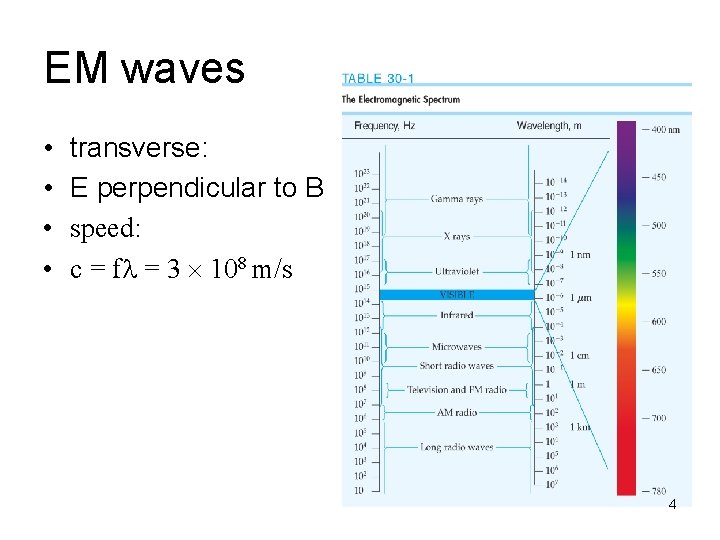
EM waves • • transverse: E perpendicular to B speed: c = fl = 3 108 m/s 4

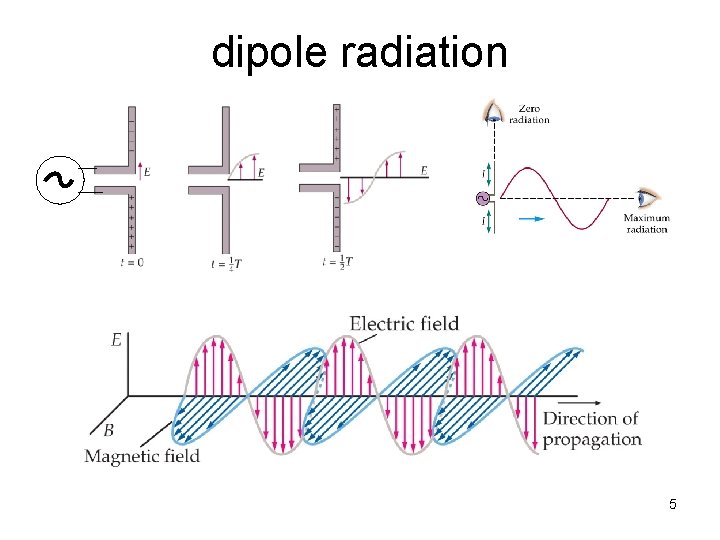
dipole radiation 5

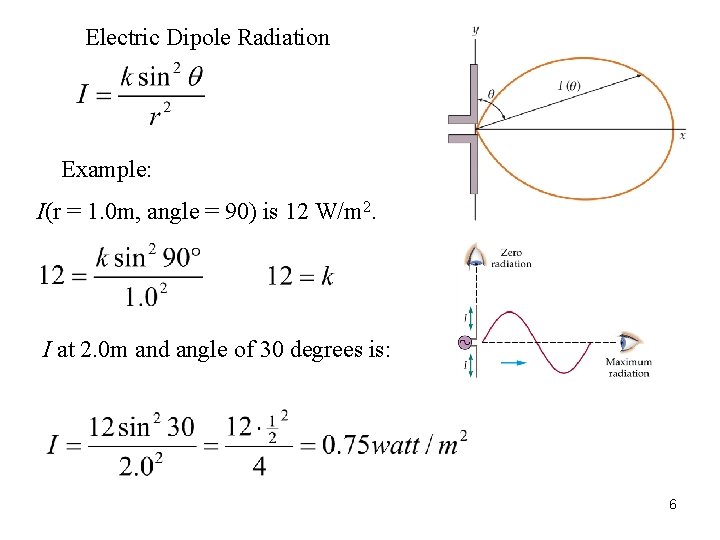
Electric Dipole Radiation Example: I(r = 1. 0 m, angle = 90) is 12 W/m 2. I at 2. 0 m and angle of 30 degrees is: 6

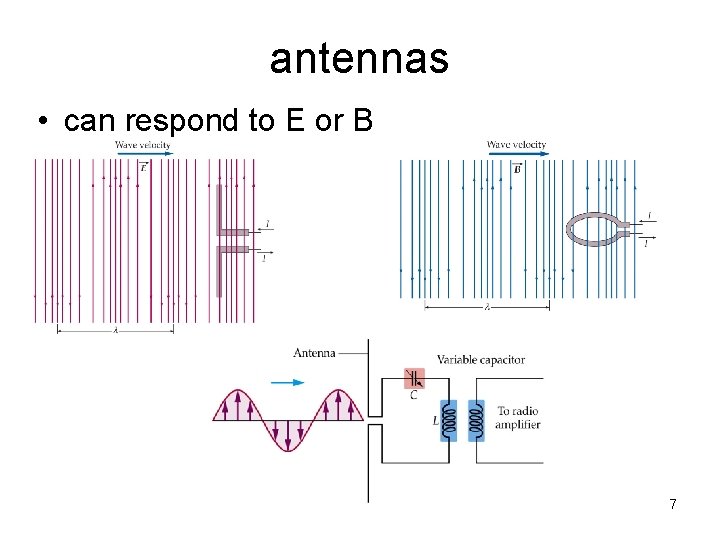
antennas • can respond to E or B 7

EM Waves • carry energy and momentum, shared equally between the electric and magnetic fields. 8
![Energy and Momentum in EM Waves Intensity energyareatime wattssq meter 9 Energy and Momentum in EM Waves • Intensity: energy/area/time [watts/sq. meter] 9](https://slidetodoc.com/presentation_image/dca33ada4e3ac191e108ceed2fc27ee5/image-9.jpg)
Energy and Momentum in EM Waves • Intensity: energy/area/time [watts/sq. meter] 9

Example 50 W Bulb • Assume that 5. 00% of the electrical power consumed by the bulb is converted to light. The average intensity at a distance of r = 1. 00 m: • The rms value of E: 10

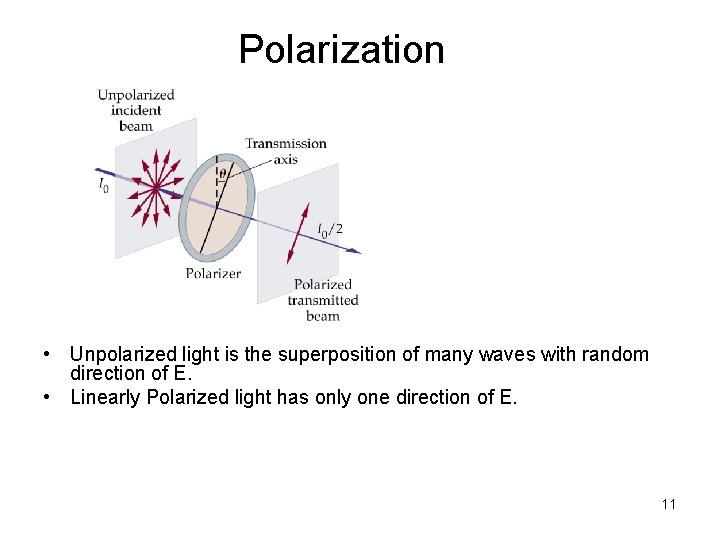
Polarization • Unpolarized light is the superposition of many waves with random direction of E. • Linearly Polarized light has only one direction of E. 11

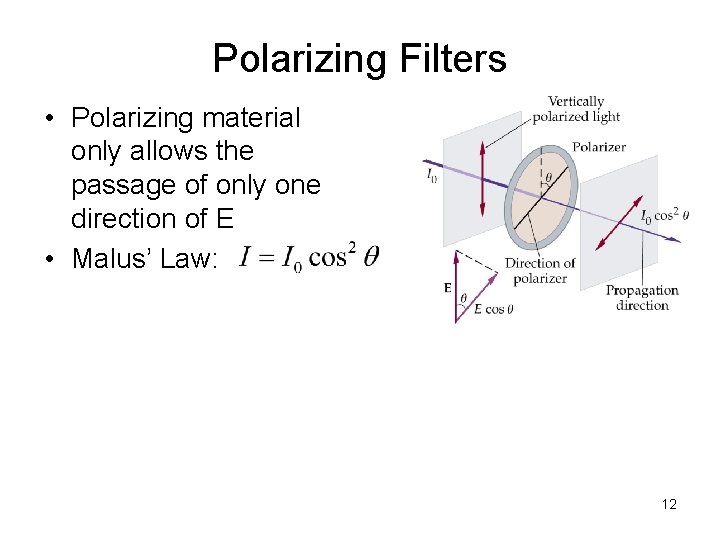
Polarizing Filters • Polarizing material only allows the passage of only one direction of E • Malus’ Law: 12

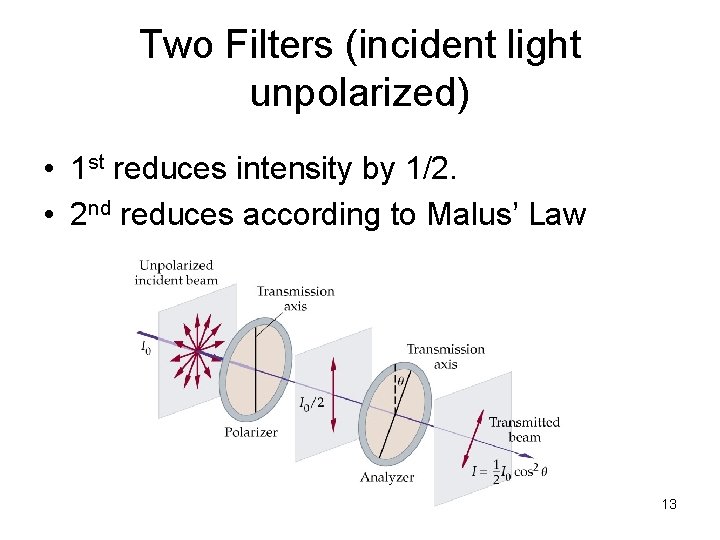
Two Filters (incident light unpolarized) • 1 st reduces intensity by 1/2. • 2 nd reduces according to Malus’ Law 13

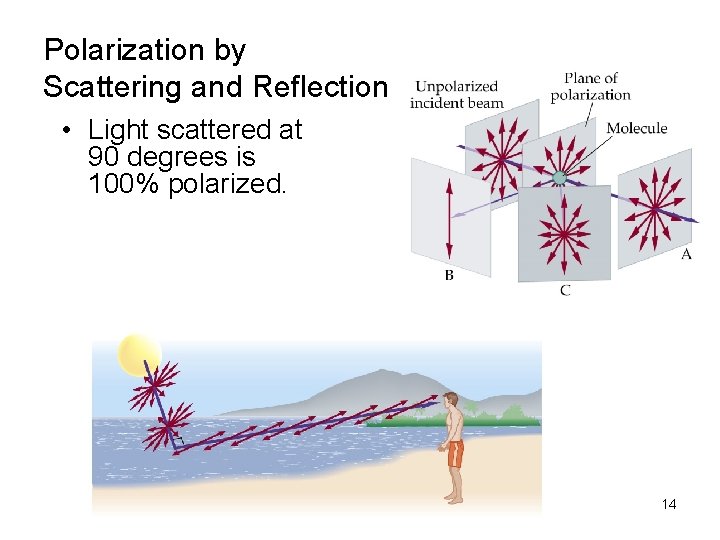
Polarization by Scattering and Reflection • Light scattered at 90 degrees is 100% polarized. 14

Summary • displacement current added to Ampere’s Law: completes Maxwell Eqs. , which explain ‘light’ properties (transverse EM wave with speed c) • visible light small segment of spectrum • energy density, intensity • polarization by reflection/scattering • Malus’ Law 15

EM waves • accelerating charges produce ‘waves’ of E and B • can be ‘pulse’ or ‘harmonic wave’ 16

Momentum • momentum = U/c The total energy received in the time by an area A The momentum received The average force Radiation pressure 17

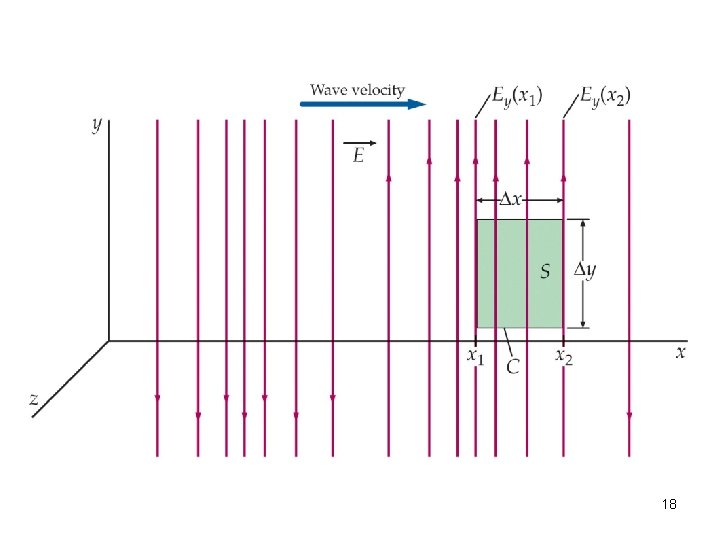
18

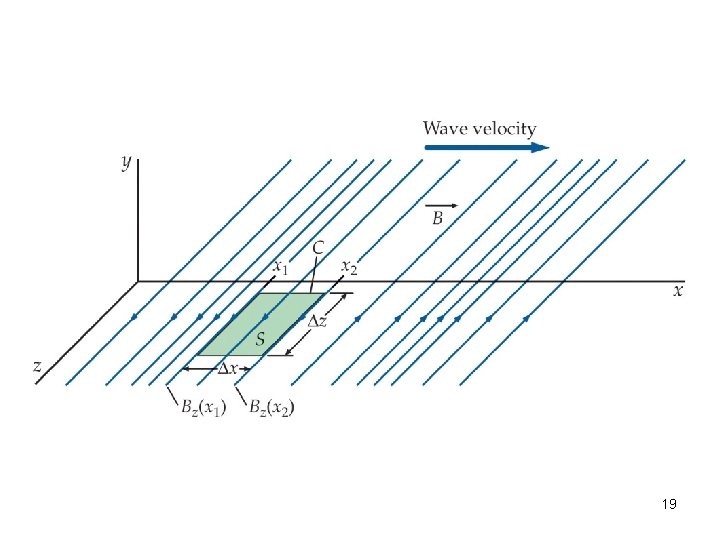
19

Example (cont. ) Part (b) 2. Use 3. Use to find 20

Example: Consider a laser that puts out an average power of P=1. 0 milliwatt in a beam having a diameter of 1. 0 mm. What is the peak amplitude of the electric field? The area of the laser beam is The electromagnetic flux S is Recall so that Substitution of the numerical values yields and thus 21