3 The optical model Prof Dr A J

3. The optical model Prof. Dr. A. J. (Arjan) Koning 1, 2 1 International 2 Division Atomic Energy Agency, Vienna of Applied Nuclear Physics, Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden Email: A. koning@iaea. org EXTEND European School on Experiment, Theory and Evaluation of Nuclear Data, Uppsala University, Sweden, August 29 - September 2, 2016

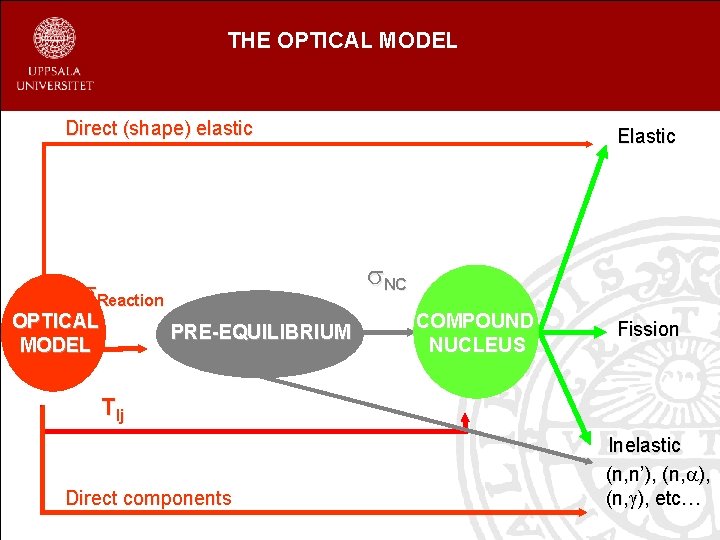
THE OPTICAL MODEL Direct (shape) elastic NC Reaction OPTICAL MODEL Elastic PRE-EQUILIBRIUM COMPOUND NUCLEUS Fission Tlj Direct components Inelastic (n, n’), (n, ), etc…

Optical model potential 3

Optical model potential 4

Optical model potential 5

THE OPTICAL MODEL Direct interaction of a projectile with a target nucleus considered as a whole Quantum model Schrödinger equation U Complex potential: U = V + i. W Refraction Absorption

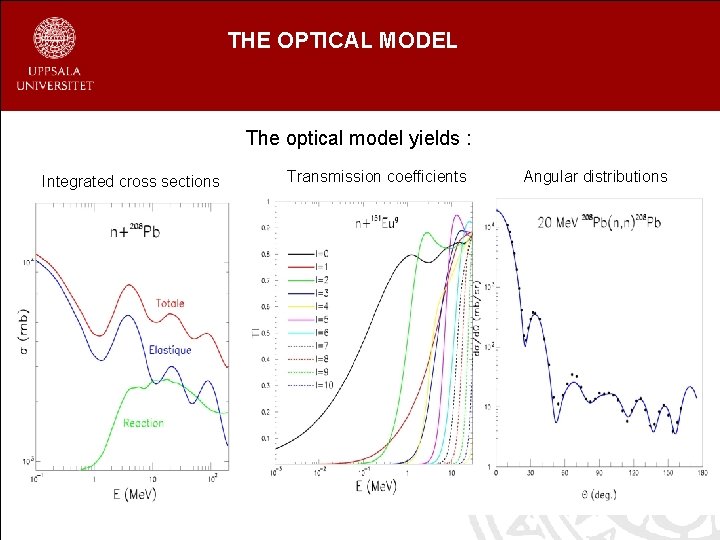
THE OPTICAL MODEL The optical model yields : Integrated cross sections Transmission coefficients Angular distributions

Two types of approaches 8

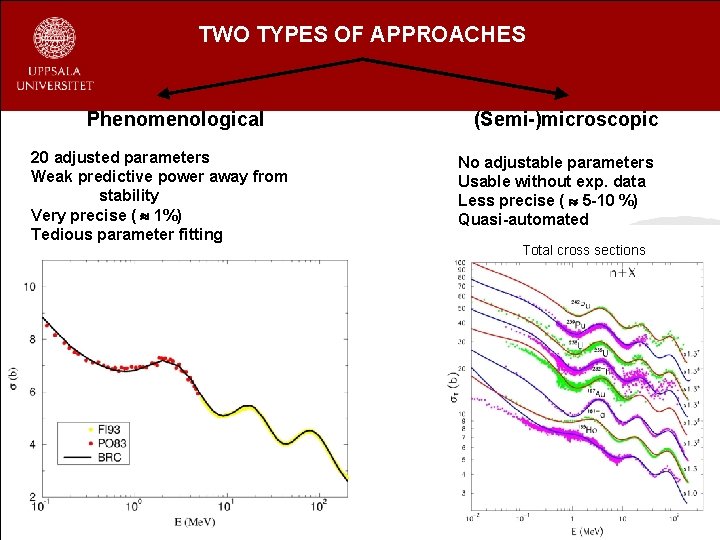
TWO TYPES OF APPROACHES Phenomenological 20 adjusted parameters Weak predictive power away from stability Very precise ( 1%) Tedious parameter fitting (Semi-)microscopic No adjustable parameters Usable without exp. data Less precise ( 5 -10 %) Quasi-automated Total cross sections

PHENOMENOLOGICAL OPTICAL MODEL f(r, R, a)= -1 1+exp((r-R)/a) g(r, R, a) = - df/dr

Phenomenological OMP 11

Standard parameterization: 0. 001 – 200 Me. V A. J. Koning and J. P. Delaroche, ``Local and global nucleon optical models from 1 ke. V to 200 Me. V'', Nucl. Phys. A 713 (2003) 231. 12

Potential depths 13

Local and global OMP Local OMP: parameter per nuclides Global OMP: mass dependent parametrization, e. g. KD 03 OMP, Nucl. Phys. A 713 (2003) 231 14

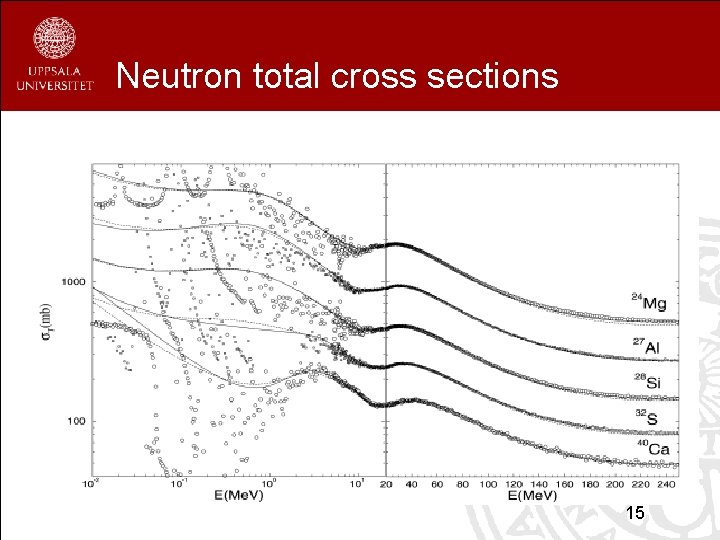
Neutron total cross sections 15

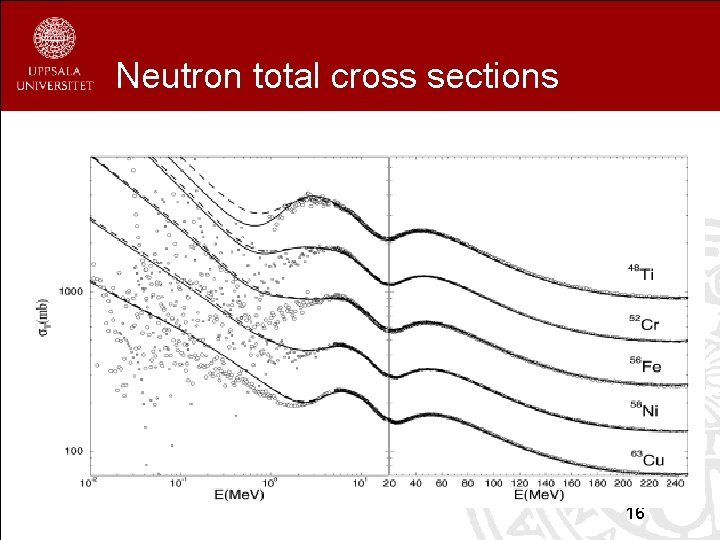
Neutron total cross sections 16

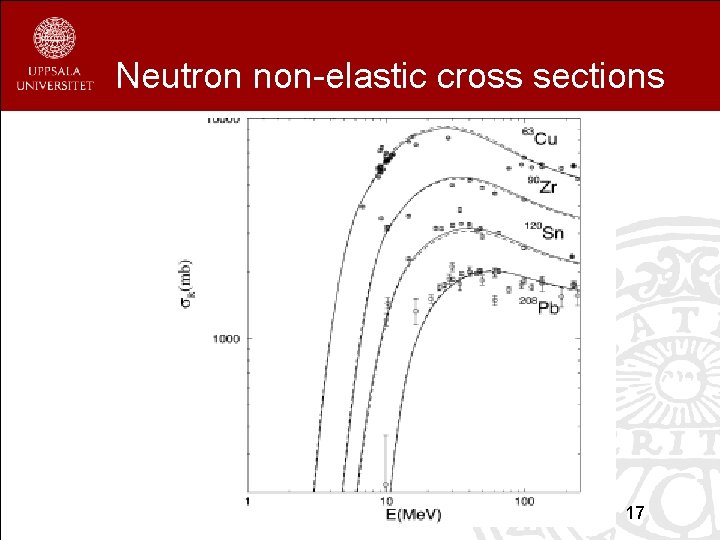
Neutron non-elastic cross sections 17

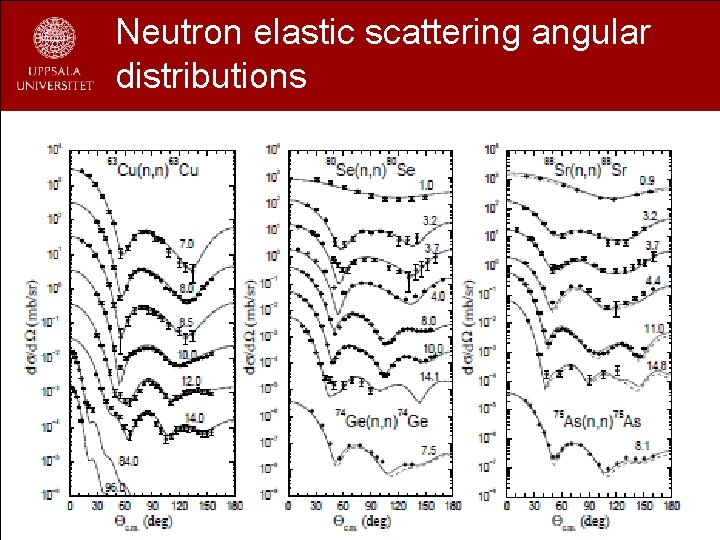
Neutron elastic scattering angular distributions 18

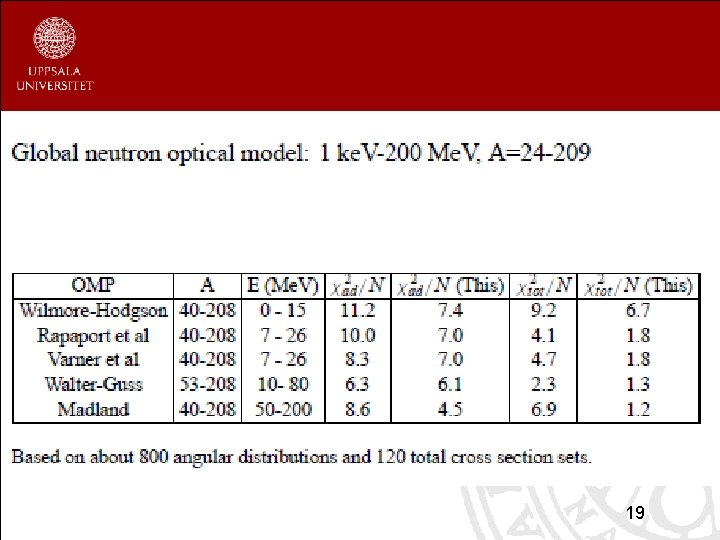
19

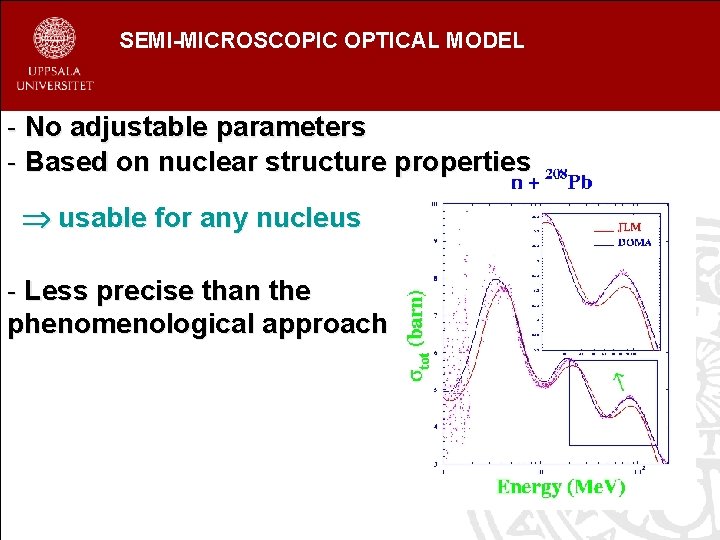
SEMI-MICROSCOPIC OPTICAL MODEL - No adjustable parameters - Based on nuclear structure properties usable for any nucleus - Less precise than the phenomenological approach

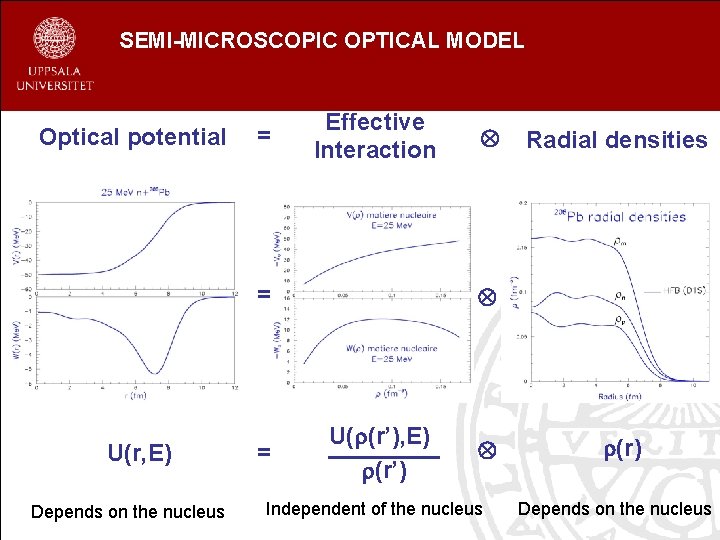
SEMI-MICROSCOPIC OPTICAL MODEL Optical potential = Effective Interaction = U(r, E) Depends on the nucleus = Radial densities U(r(r’), E) r(r’) Independent of the nucleus r(r) Depends on the nucleus

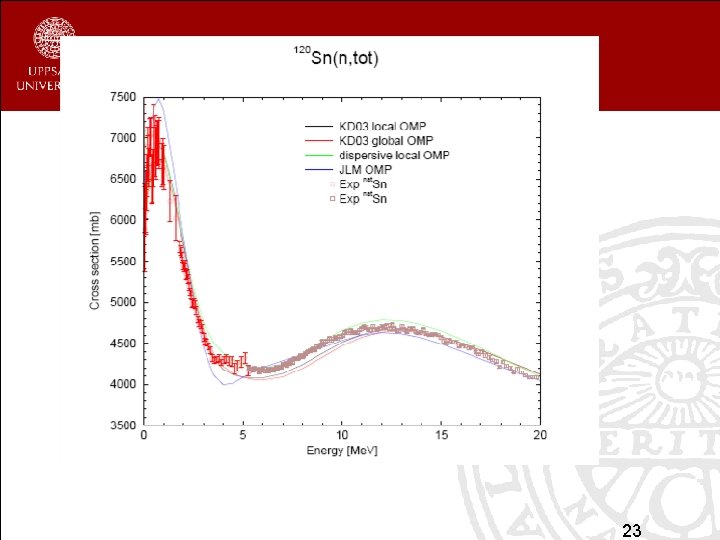
Sample 16: optical model for 120 Sn • Study impact of changing parameters • talys < input >output (about 20 -30 seconds) • cp totalxs. org • Edit the input file and add the following line: rvadjust n 1. 05 This means: increase the radius of the real volume potential by 5% • xmgrace totalxs. org (to see the difference) • TALYS has 250 parameters like this (RT*M) 22

23

Towards a complete calculation for Cu-65: Optical model • Copy previous sample case for Sn-120, and change into Cu-65 • talys < input >output • Retrieve experimental data for total cross sections from EXFOR at IAEA and compare. • Sample case 16 has 4 different sub-cases, for 4 different OMP’s. See what the effect is for Cu-65 (i. e. 4 TALYS curves) 24