3 Project Management Power Point presentation to accompany

3 Project Management Power. Point presentation to accompany Heizer and Render Operations Management, 10 e Principles of Operations Management, 8 e Power. Point slides by Jeff Heyl © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -1

Project Characteristics u One of a kind u Many related activities u Precedent constraints u General purpose equipment u High labor skills © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -2

Examples of Projects u Building Construction u Research Project © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -3

Management of Projects 1. Planning - goal setting, defining the project, team organization 2. Scheduling - relates people, money, and supplies to specific activities and activities to each other 3. Controlling - monitors resources, costs, quality, and budgets; revises plans and shifts resources to meet time and cost demands © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -4

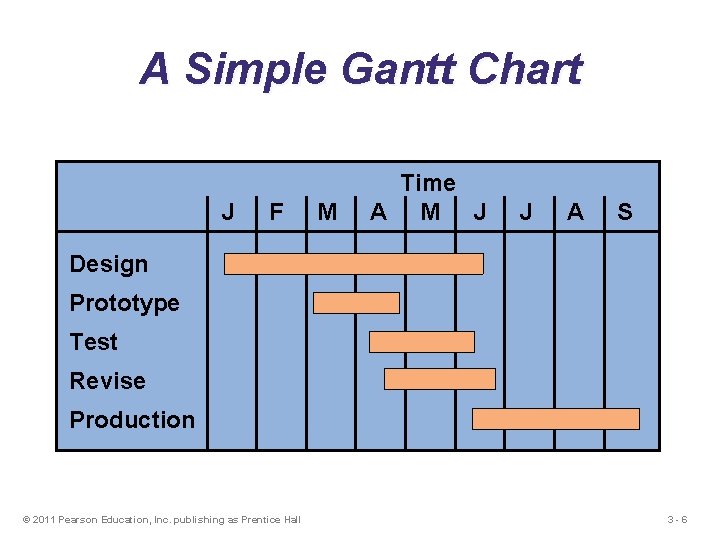
Project Management Techniques u Gantt chart u Critical Path Method (CPM) u Program Evaluation and Review Technique (PERT) © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -5

A Simple Gantt Chart J F M Time A M J J A S Design Prototype Test Revise Production © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -6

PERT and CPM u Network techniques u Developed in 1950’s u CPM by Du. Pont for chemical plants (1957) u PERT by Booz, Allen & Hamilton with the U. S. Navy, for Polaris missile (1958) u Consider precedence relationships and interdependencies u Each uses a different estimate of activity times © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -7

Six Steps PERT & CPM 1. Define the project and prepare the work breakdown structure 2. Develop relationships among the activities - decide which activities must precede and which must follow others 3. Draw the network connecting all of the activities © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -8

Six Steps PERT & CPM 4. Assign time and/or cost estimates to each activity 5. Compute the longest time path through the network – this is called the critical path 6. Use the network to help plan, schedule, monitor, and control the project © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 -9

Questions PERT & CPM Can Answer 1. When will the entire project be completed? 2. What are the critical activities or tasks in the project? 3. Which are the noncritical activities? 4. What is the probability the project will be completed by a specific date? © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 10

Questions PERT & CPM Can Answer 5. Is the project on schedule, behind schedule, or ahead of schedule? 6. Is the money spent equal to, less than, or greater than the budget? 7. Are there enough resources available to finish the project on time? 8. If the project must be finished in a shorter time, what is the way to accomplish this at least cost? © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 11

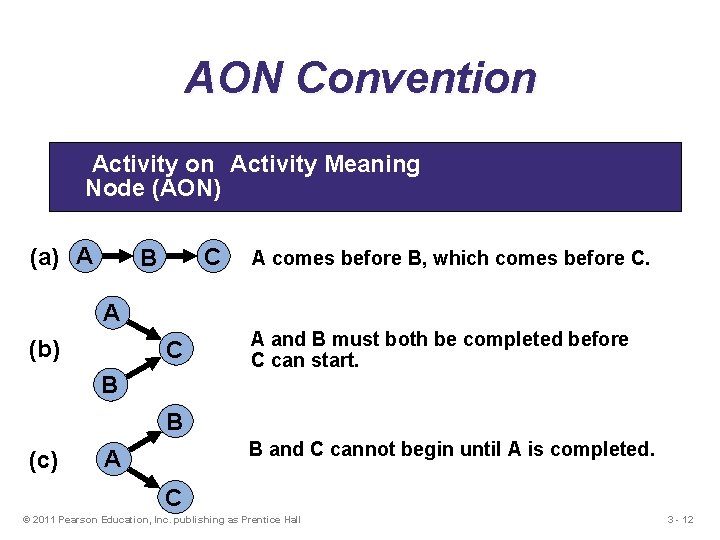
AON Convention Activity Meaning Node (AON) (a) A C B A comes before B, which comes before C. A (b) C A and B must both be completed before C can start. B B (c) B and C cannot begin until A is completed. A C © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 12

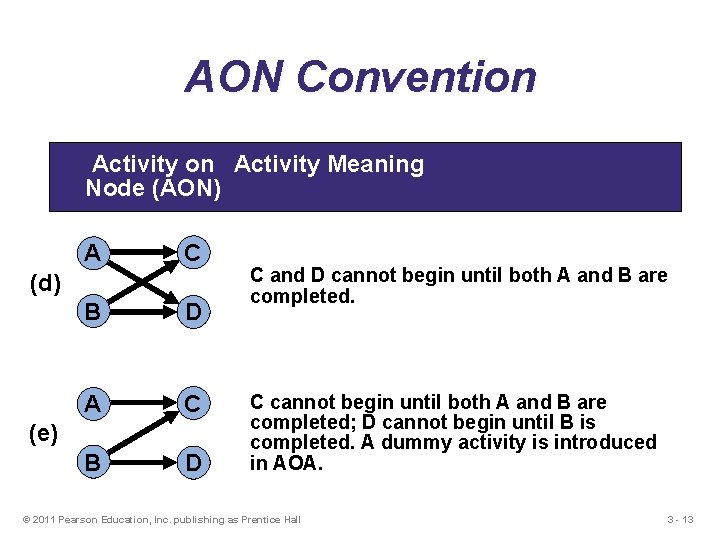
AON Convention Activity Meaning Node (AON) A C B D (d) (e) C and D cannot begin until both A and B are completed. C cannot begin until both A and B are completed; D cannot begin until B is completed. A dummy activity is introduced in AOA. © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 13

AON Convention Activity Meaning Node (AON) A B (f) C D B and C cannot begin until A is completed. D cannot begin until both B and C are completed. A dummy activity is again introduced in AOA. © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 14

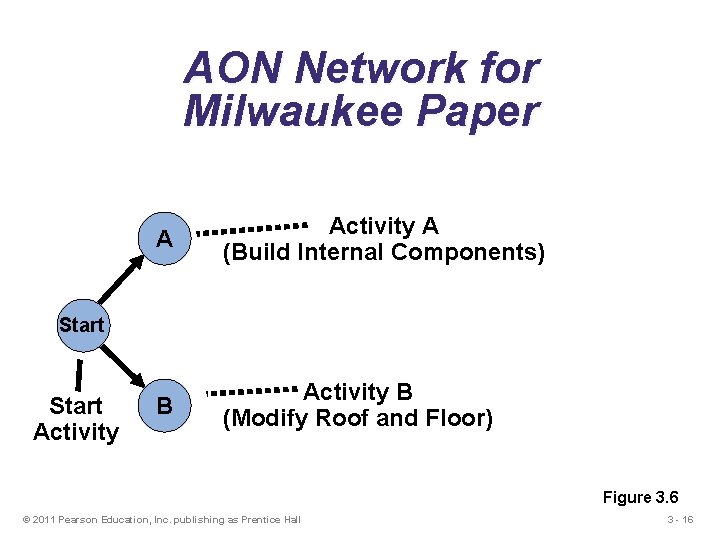
AON Example Milwaukee Paper Manufacturing's Activities and Predecessors Activity A Description Build internal components Immediate Predecessors — B Modify roof and floor — C Construct collection stack A D Pour concrete and install frame A, B E Build high-temperature burner C F Install pollution control system C G Install air pollution device D, E H Inspect and test F, G Table 3. 1 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 15

AON Network for Milwaukee Paper A Activity A (Build Internal Components) B Activity B (Modify Roof and Floor) Start Activity Figure 3. 6 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 16

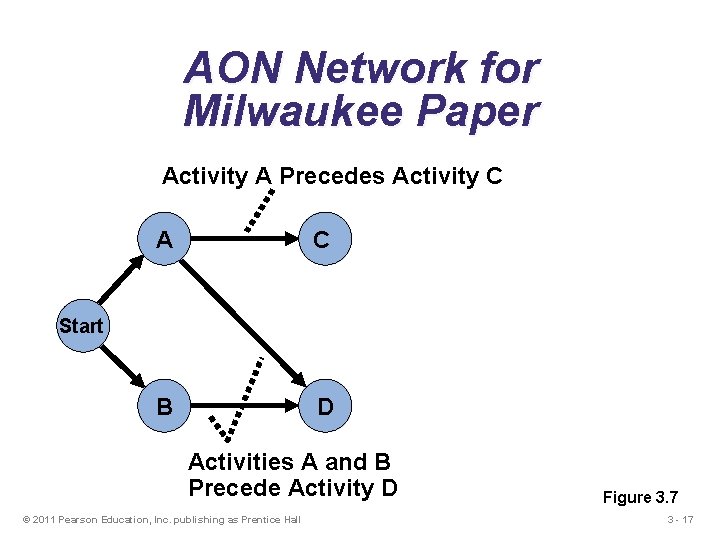
AON Network for Milwaukee Paper Activity A Precedes Activity C A C B D Start Activities A and B Precede Activity D © 2011 Pearson Education, Inc. publishing as Prentice Hall Figure 3. 7 3 - 17

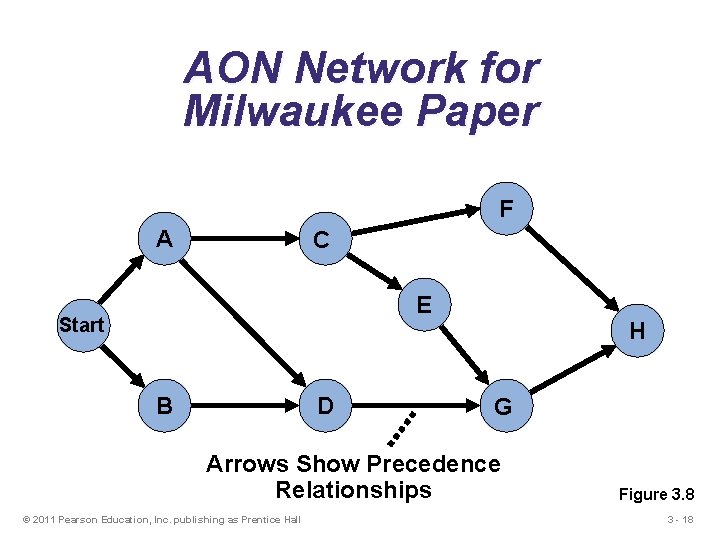
AON Network for Milwaukee Paper F A C E Start B D H G Arrows Show Precedence Relationships © 2011 Pearson Education, Inc. publishing as Prentice Hall Figure 3. 8 3 - 18

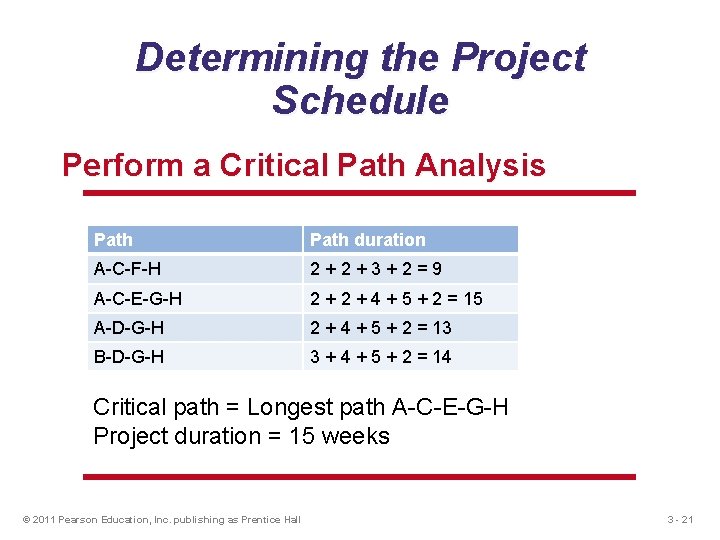
Determining the Project Schedule Perform a Critical Path Analysis u The critical path is the longest path through the network u The critical path is the shortest time in which the project can be completed u Any delay in critical path activities delays the project u Critical path activities have no slack time © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 19

Determining the Project Schedule Perform a Critical Path Analysis Activity A B C D E F G H Description Time (weeks) Build internal components 2 Modify roof and floor 3 Construct collection stack 2 Pour concrete and install frame 4 Build high-temperature burner 4 Install pollution control system 3 Install air pollution device 5 Inspect and test 2 Total Time (weeks) 25 Table 3. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 20

Determining the Project Schedule Perform a Critical Path Analysis Path duration A-C-F-H 2+2+3+2=9 A-C-E-G-H 2 + 4 + 5 + 2 = 15 A-D-G-H 2 + 4 + 5 + 2 = 13 B-D-G-H 3 + 4 + 5 + 2 = 14 Critical path = Longest path A-C-E-G-H Project duration = 15 weeks © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 21

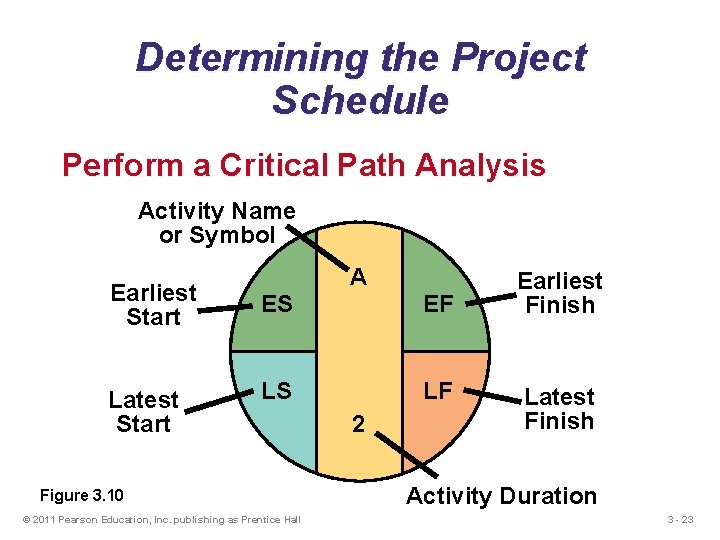
Determining the Project Schedule Perform a Critical Path Analysis Earliest start (ES) = earliest time at which an activity can Activity Description Time (weeks) start, assuming all predecessors have A Build internal components 2 been completed Modify roof and floor 3 Earliest. Bfinish (EF) = earliest time at which an activity can be finished C Construct collection stack 2 D start (LS) Pour=concrete and 4 Latest latest time atinstall which frame an activity can start so as to not delay E Build high-temperature burnerthe completion 4 of thecontrol entire project F Install time pollution system 3 Latest. Gfinish (LF) = latest time bydevice which an activity has Install air pollution 5 to be finished so as to not delay the H Inspect and test 2 completion time of the entire project Total Time (weeks) 25 Table 3. 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 22

Determining the Project Schedule Perform a Critical Path Analysis Activity Name or Symbol A Earliest Start ES EF Latest Start LS LF Figure 3. 10 © 2011 Pearson Education, Inc. publishing as Prentice Hall 2 Earliest Finish Latest Finish Activity Duration 3 - 23

Forward Pass Begin at starting event and work forward Earliest Start Time Rule: u If an activity has only a single immediate predecessor, its ES equals the EF of the predecessor u If an activity has multiple immediate predecessors, its ES is the maximum of all the EF values of its predecessors ES = Max {EF of all immediate predecessors} © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 24

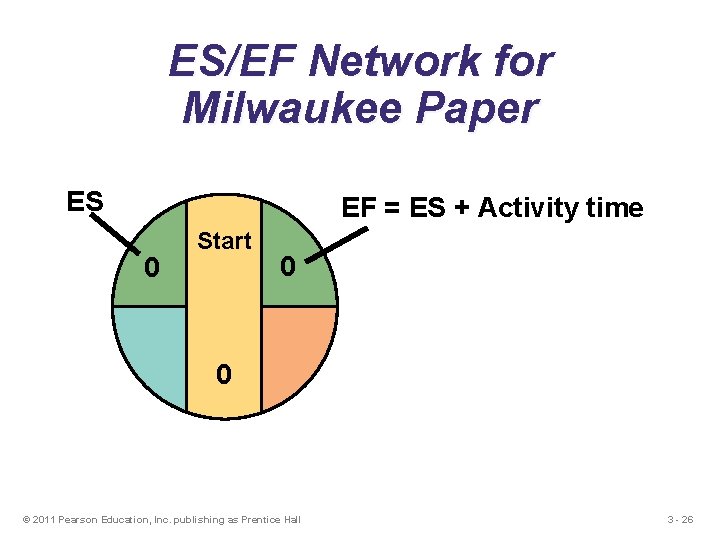
Forward Pass Begin at starting event and work forward Earliest Finish Time Rule: u The earliest finish time (EF) of an activity is the sum of its earliest start time (ES) and its activity time EF = ES + Activity time © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 25

ES/EF Network for Milwaukee Paper ES EF = ES + Activity time 0 Start 0 0 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 26

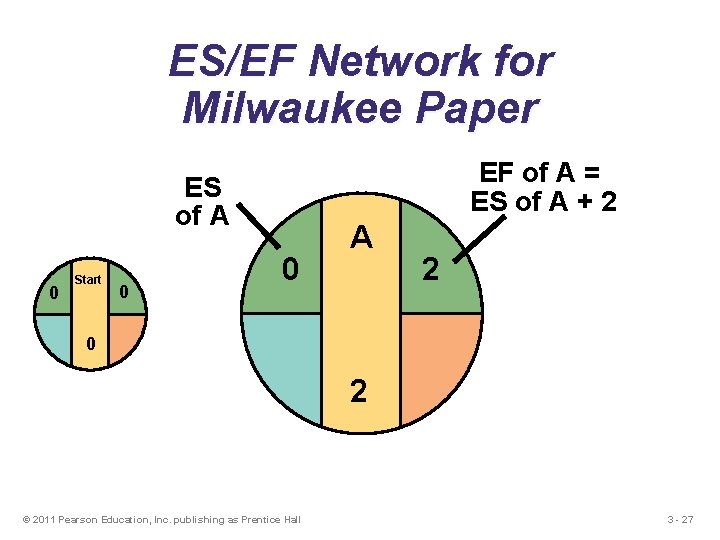
ES/EF Network for Milwaukee Paper EF of A = ES of A + 2 ES of A 0 Start 0 0 A 2 0 2 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 27

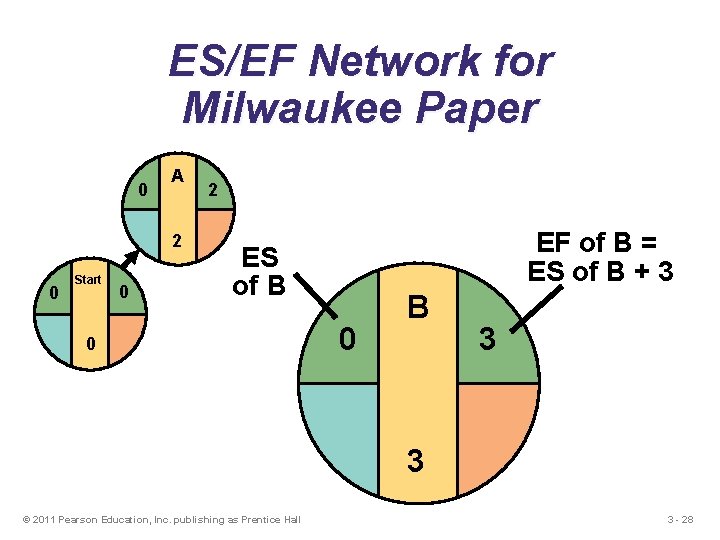
ES/EF Network for Milwaukee Paper 0 A 2 0 Start 0 2 EF of B = ES of B + 3 ES of B 0 0 B 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 28

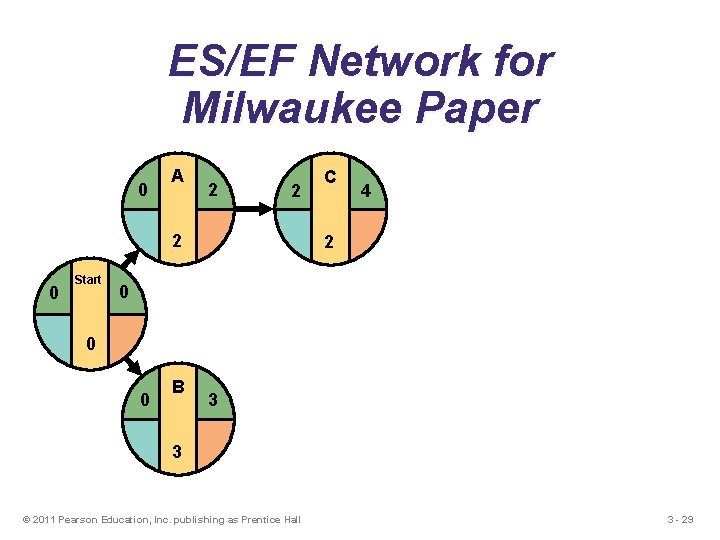
ES/EF Network for Milwaukee Paper 0 A 2 2 2 0 Start C 4 2 0 0 0 B 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 29

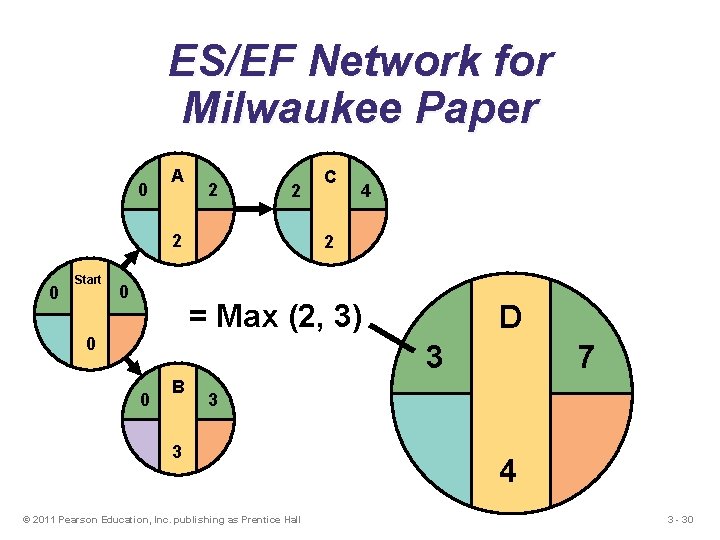
ES/EF Network for Milwaukee Paper 0 A 2 2 2 0 Start 0 C 4 2 = Max (2, 3) 0 D 3 0 B 7 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall 4 3 - 30

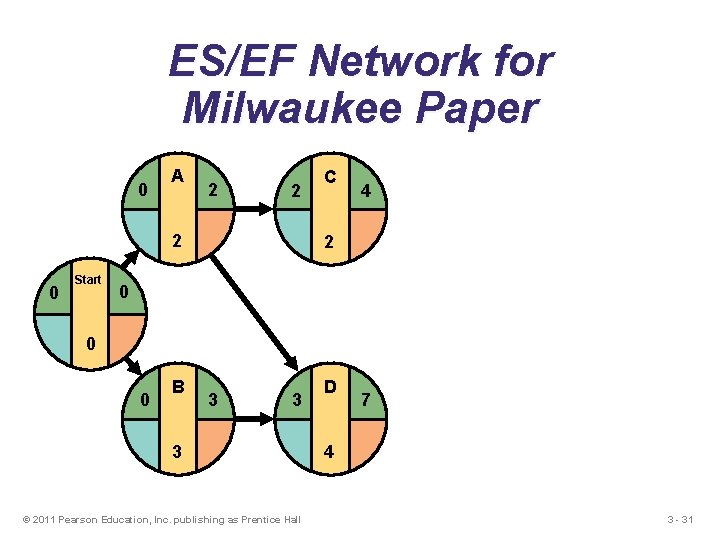
ES/EF Network for Milwaukee Paper 0 A 2 2 2 0 Start C 4 2 0 0 0 B 3 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D 7 4 3 - 31

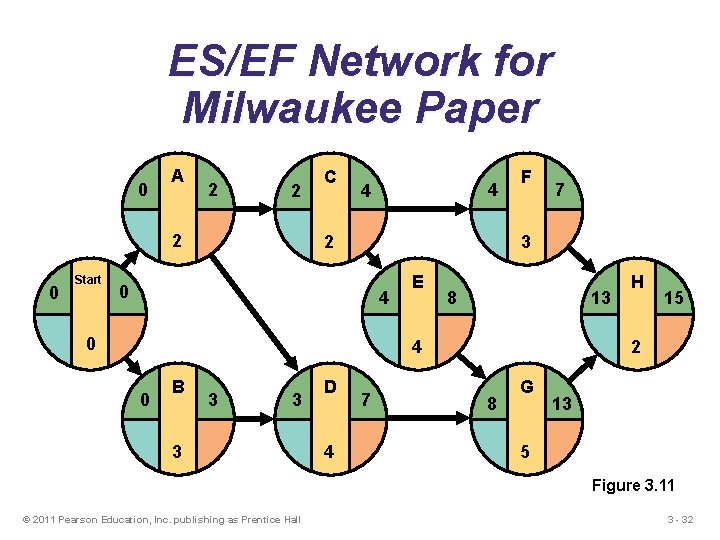
ES/EF Network for Milwaukee Paper 0 A 2 2 2 0 Start C 4 4 2 F 7 3 0 4 0 E 8 13 4 0 B 3 3 3 D 4 7 H 15 2 8 G 13 5 Figure 3. 11 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 32

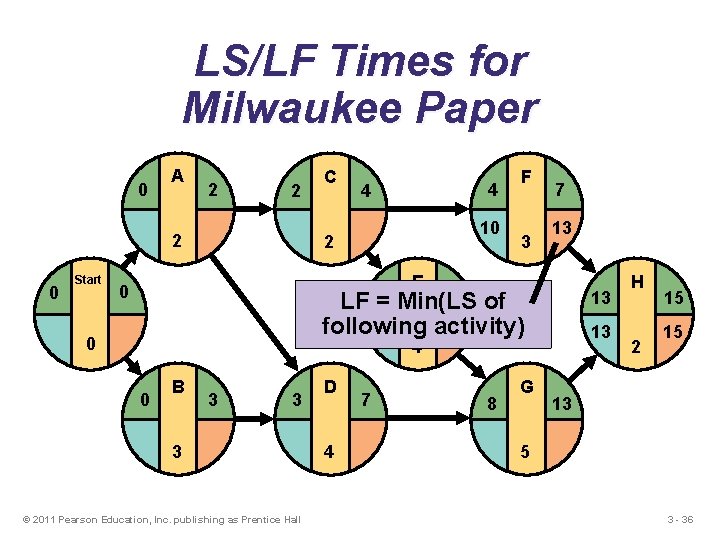
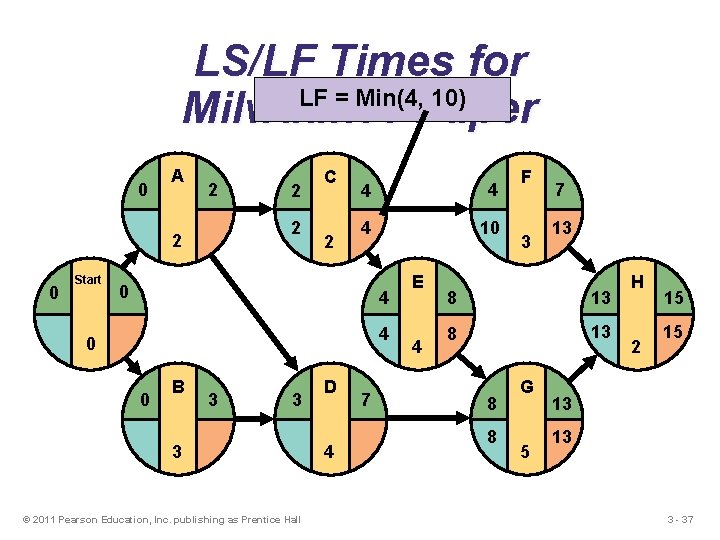
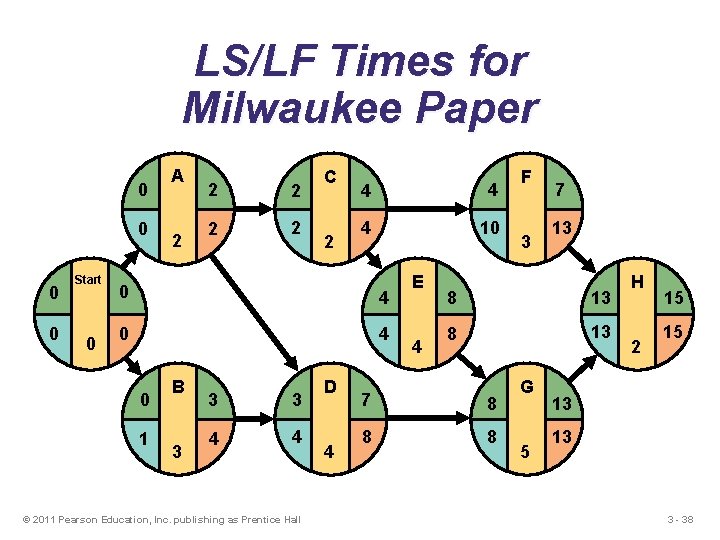
Backward Pass Begin with the last event and work backwards Latest Finish Time Rule: u If an activity is an immediate predecessor for just a single activity, its LF equals the LS of the activity that immediately follows it u If an activity is an immediate predecessor to more than one activity, its LF is the minimum of all LS values of all activities that immediately follow it LF = Min {LS of all immediate following activities} © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 33

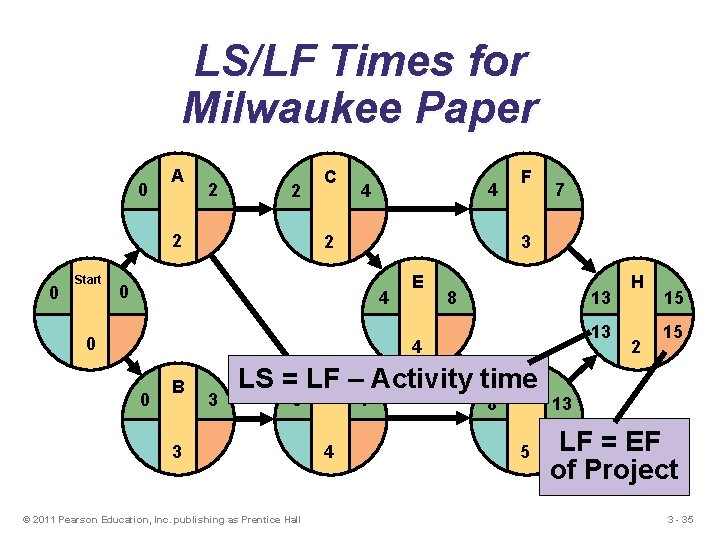
Backward Pass Begin with the last event and work backwards Latest Start Time Rule: u The latest start time (LS) of an activity is the difference of its latest finish time (LF) and its activity time LS = LF – Activity time © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 34

LS/LF Times for Milwaukee Paper 0 A 2 2 2 0 Start C 4 4 2 F 7 3 0 4 0 E 8 13 13 4 0 B 3 LS = LF D – Activity time G 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall 7 4 8 5 H 2 15 15 13 LF = EF of Project 3 - 35

LS/LF Times for Milwaukee Paper 0 A 2 2 2 0 Start C 4 4 10 2 F 3 7 13 E 0 8 of LF =4 Min(LS following activity) 0 13 13 4 0 B 3 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D 4 7 8 G H 2 15 15 13 5 3 - 36

LS/LF Times for LF = Min(4, 10) Milwaukee Paper 0 A 2 2 2 0 Start 2 C 2 4 4 4 10 0 4 4 0 0 B 3 3 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall D 4 7 E 4 F 3 7 13 8 8 G 5 H 2 15 15 13 13 3 - 37

LS/LF Times for Milwaukee Paper 0 0 Start 0 A 2 2 2 C 2 4 4 4 10 0 4 0 1 B 3 3 3 4 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall D 4 E 4 F 3 7 13 8 13 7 8 8 8 G 5 H 2 15 15 13 13 3 - 38

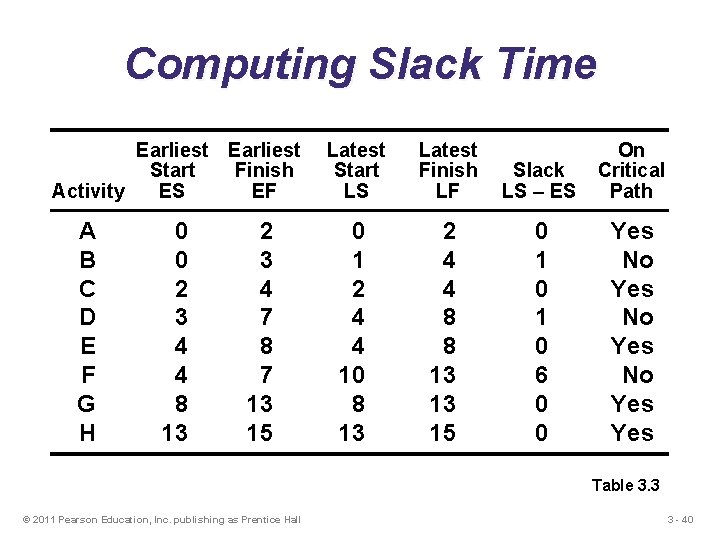
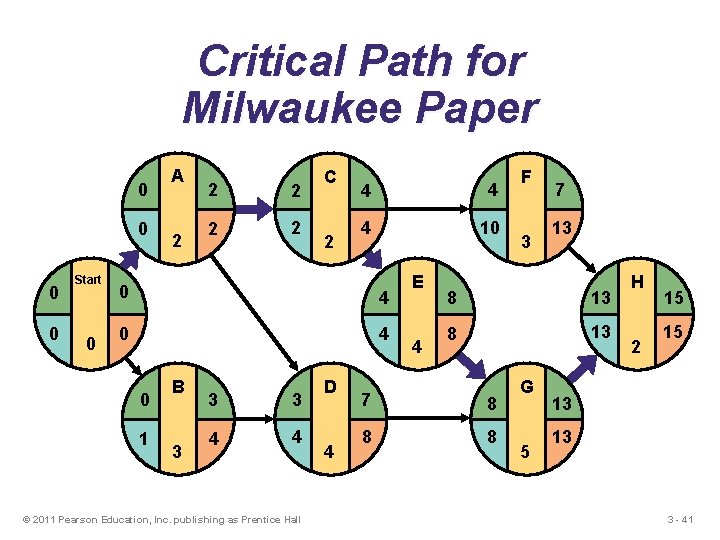
Computing Slack Time After computing the ES, EF, LS, and LF times for all activities, compute the slack or free time for each activity u Slack is the length of time an activity can be delayed without delaying the entire project Slack = LS – ES © 2011 Pearson Education, Inc. publishing as Prentice Hall or Slack = LF – EF 3 - 39

Computing Slack Time Earliest Start Finish Activity ES EF A B C D E F G H 0 0 2 3 4 4 8 13 2 3 4 7 8 7 13 15 Latest Start LS Latest Finish LF Slack LS – ES On Critical Path 0 1 2 4 4 10 8 13 2 4 4 8 8 13 13 15 0 1 0 6 0 0 Yes No Yes Table 3. 3 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 40

Critical Path for Milwaukee Paper 0 0 Start 0 A 2 2 2 C 2 4 4 4 10 0 4 0 1 B 3 3 3 4 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall D 4 E 4 F 3 7 13 8 13 7 8 8 8 G 5 H 2 15 15 13 13 3 - 41

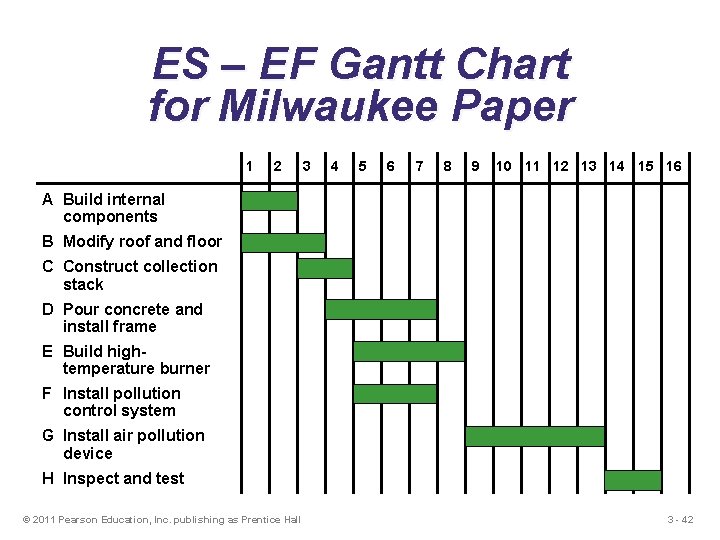
ES – EF Gantt Chart for Milwaukee Paper 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A Build internal components B Modify roof and floor C Construct collection stack D Pour concrete and install frame E Build hightemperature burner F Install pollution control system G Install air pollution device H Inspect and test © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 42

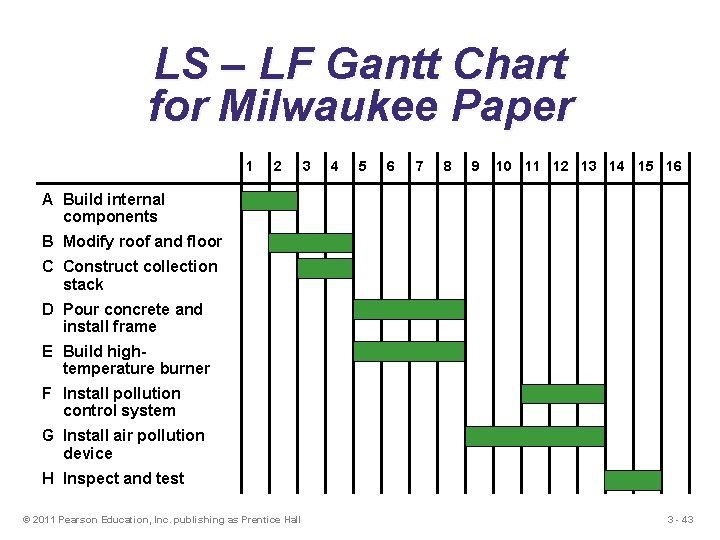
LS – LF Gantt Chart for Milwaukee Paper 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 A Build internal components B Modify roof and floor C Construct collection stack D Pour concrete and install frame E Build hightemperature burner F Install pollution control system G Install air pollution device H Inspect and test © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 43

Variability in Activity Times u CPM assumes we know a fixed time estimate for each activity and there is no variability in activity times u PERT uses a probability distribution for activity times to allow for variability © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 44

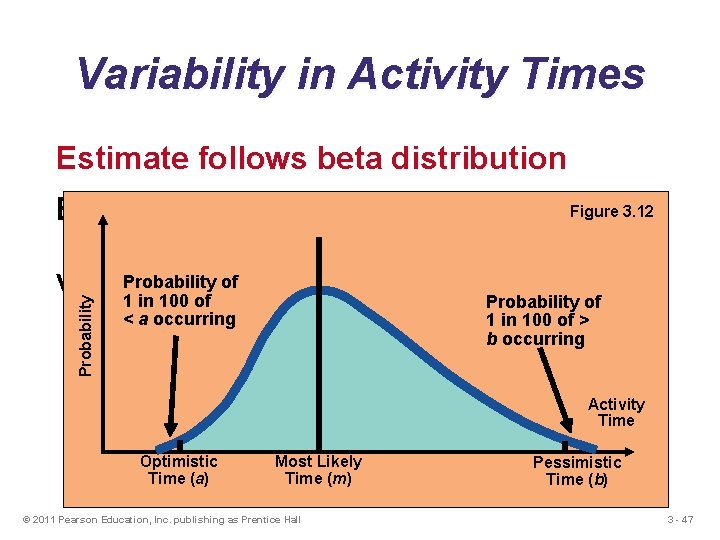
Variability in Activity Times u Three time estimates are required u Optimistic time (a) – if everything goes according to plan u Pessimistic time (b) – assuming very unfavorable conditions u Most likely time (m) – most realistic estimate © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 45

Variability in Activity Times Estimate follows beta distribution Expected time: t = (a + 4 m + b)/6 Variance of times: v = [(b – a)/6]2 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 46

Variability in Activity Times Estimate follows beta distribution Probability Figure 3. 12 Expected time: t = (a + 4 m + b)/6 Probability oftimes: Variance of 1 in 100 of Probability of < a occurring v = [(b − a)/6]2 1 in 100 of > b occurring Activity Time Optimistic Time (a) Most Likely Time (m) © 2011 Pearson Education, Inc. publishing as Prentice Hall Pessimistic Time (b) 3 - 47

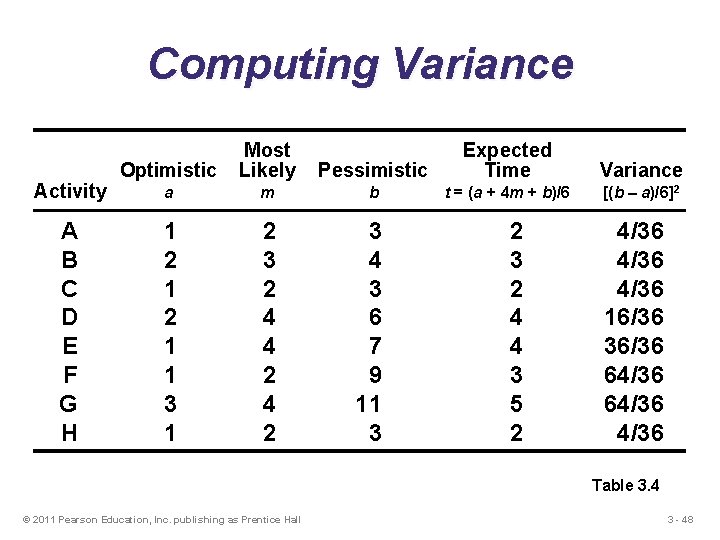
Computing Variance Activity A B C D E F G H Optimistic Most Likely Pessimistic Expected Time Variance a m b t = (a + 4 m + b)/6 [(b – a)/6]2 1 2 1 1 3 1 2 3 2 4 4 2 3 4 3 6 7 9 11 3 2 4 4 3 5 2 4/36 16/36 36/36 64/36 Table 3. 4 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 48

Probability of Project Completion Project variance is computed by summing the variances of critical activities sp 2 = Project variance = (variances of activities on critical path) © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 49

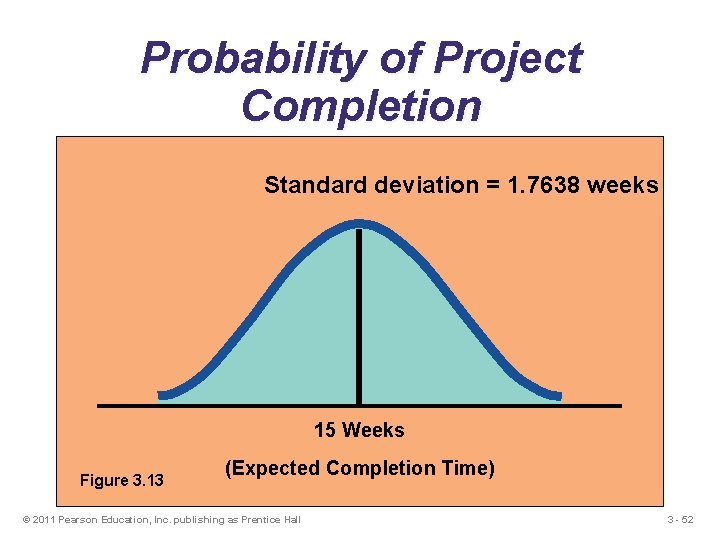
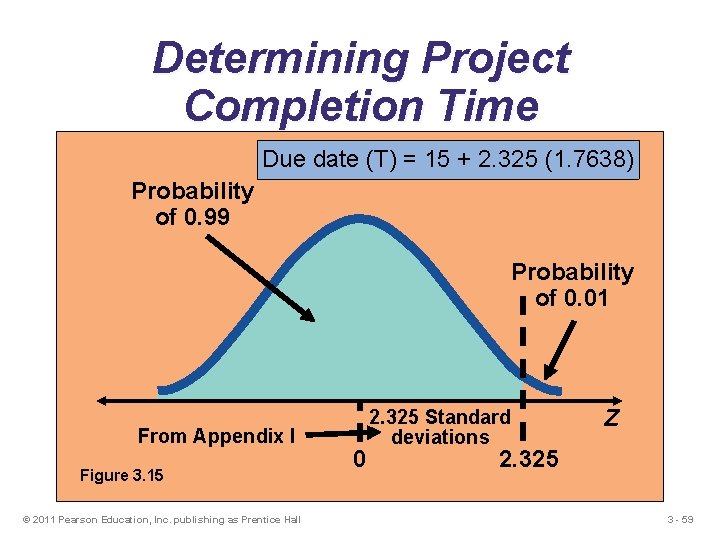
Probability of Project Completion Project variance is computed by summing the variances of critical Project variance activities s 2 p = 4/36 + 36/36 + 64/36 + 4/36 = 112/36 = 3. 1111 Project standard deviation sp = = Project variance 3. 1111 = 1. 7638 weeks © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 50

Probability of Project Completion PERT makes two more observations: u Total project completion times follow a normal probability distribution u Activity times are statistically independent © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 51

Probability of Project Completion Standard deviation = 1. 7638 weeks 15 Weeks Figure 3. 13 (Expected Completion Time) © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 52

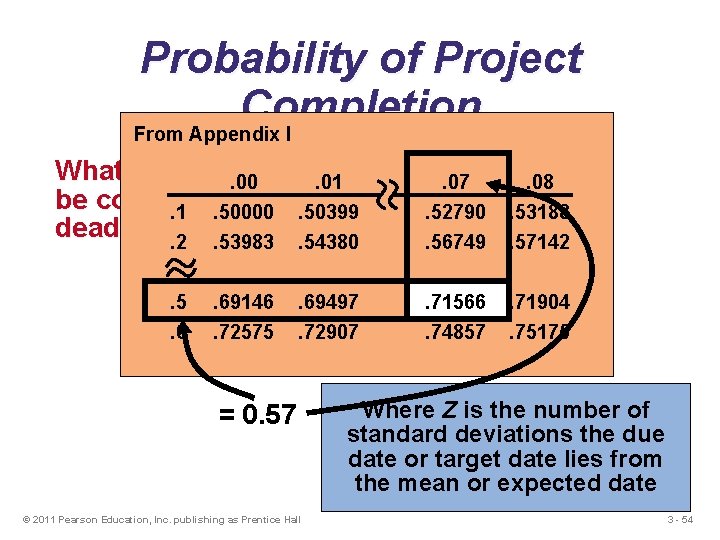
Probability of Project Completion What is the probability this project can be completed on or before the 16 week deadline? Where Z is the Z= number of standard TE = Expected project completion time deviations the T = Due date due date or target date lies from the Z = (16 – 15)/1. 7638 mean or expected date = 0. 57 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 53

Probability of Project Completion From Appendix I What is the probability can. 00. 01 this project. 07. 08 be completed on or before the 16 week. 1. 50000. 50399. 52790. 53188 deadline? . 2. 53983. 54380. 56749. 57142. 5. 6 due − expected date /s Z. 69146 = date. 69497. 71566. 71904 p of completion. 72575 . 72907 . 74857 . 75175 = (16 wks − 15 wks)/1. 76 = 0. 57 © 2011 Pearson Education, Inc. publishing as Prentice Hall Where Z is the number of standard deviations the due date or target date lies from the mean or expected date 3 - 54

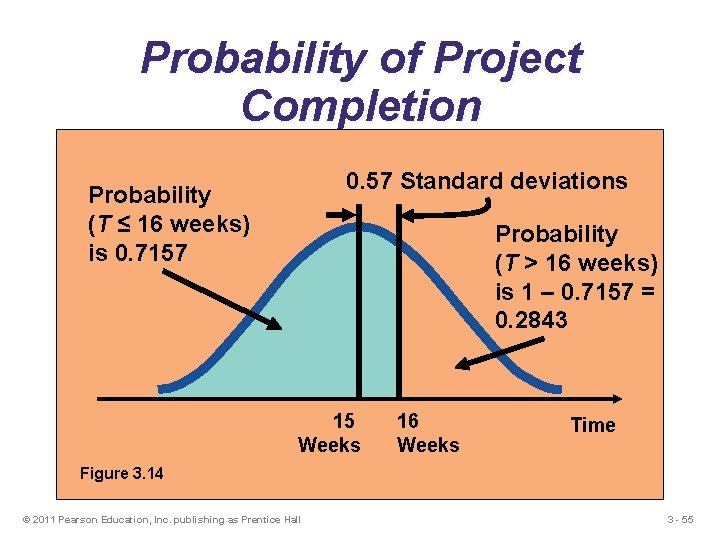
Probability of Project Completion 0. 57 Standard deviations Probability (T ≤ 16 weeks) is 0. 7157 Probability (T > 16 weeks) is 1 – 0. 7157 = 0. 2843 15 Weeks 16 Weeks Time Figure 3. 14 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 55

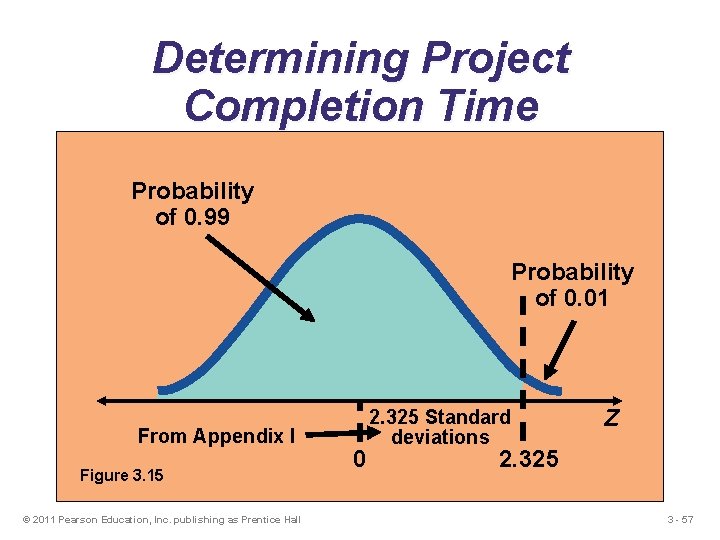
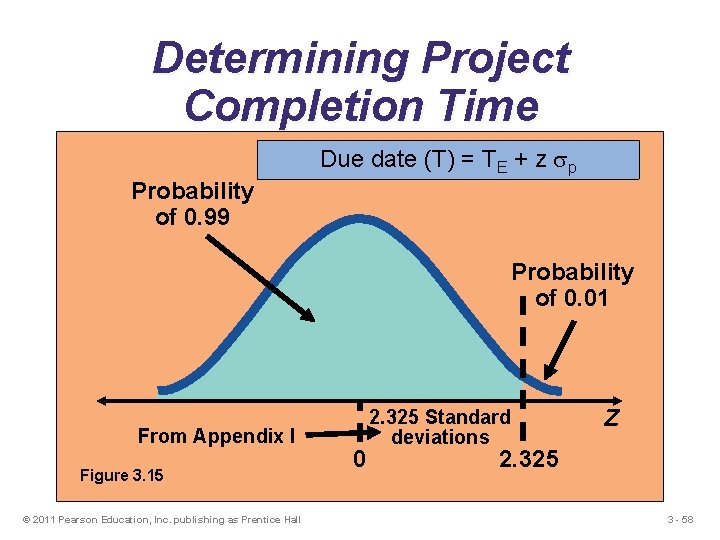
Project Completion for given confidence Determine a due date for the project completion time that will have a 99% probability of meeting. Due date = TE + Z sp © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 56

Determining Project Completion Time Probability of 0. 99 Probability of 0. 01 From Appendix I Figure 3. 15 © 2011 Pearson Education, Inc. publishing as Prentice Hall 0 2. 325 Standard deviations Z 2. 325 3 - 57

Determining Project Completion Time Due date (T) = TE + z sp Probability of 0. 99 Probability of 0. 01 From Appendix I Figure 3. 15 © 2011 Pearson Education, Inc. publishing as Prentice Hall 0 2. 325 Standard deviations Z 2. 325 3 - 58

Determining Project Completion Time Due date (T) = 15 + 2. 325 (1. 7638) Probability of 0. 99 Probability of 0. 01 From Appendix I Figure 3. 15 © 2011 Pearson Education, Inc. publishing as Prentice Hall 0 2. 325 Standard deviations Z 2. 325 3 - 59

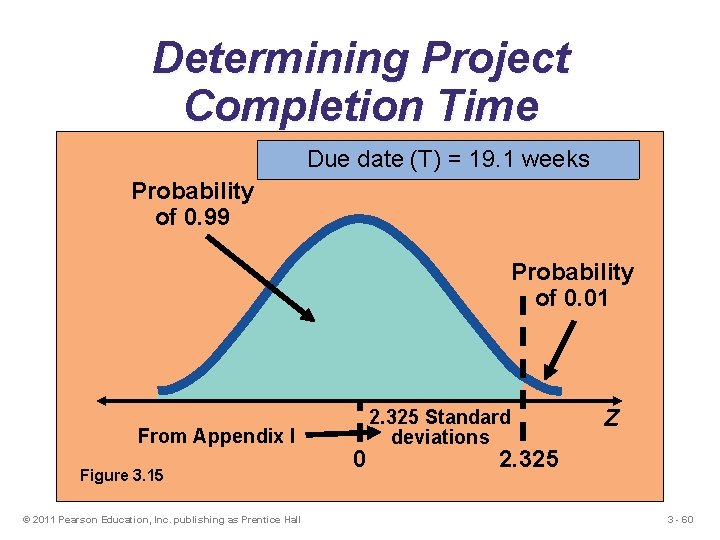
Determining Project Completion Time Due date (T) = 19. 1 weeks Probability of 0. 99 Probability of 0. 01 From Appendix I Figure 3. 15 © 2011 Pearson Education, Inc. publishing as Prentice Hall 0 2. 325 Standard deviations Z 2. 325 3 - 60

Variability of Completion Time for Noncritical Paths u Variability of times for activities on noncritical paths must be considered when finding the probability of finishing in a specified time u Variation in noncritical activity may cause change in critical path © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 61

What Project Management Has Provided So Far 1. The project’s expected completion time is 15 weeks 2. There is a 71. 57% chance the equipment will be in place by the 16 week deadline 3. Five activities (A, C, E, G, and H) are on the critical path 4. Three activities (B, D, F) are not on the critical path and have slack time 5. A detailed schedule is available © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 62

Trade-Offs and Project Crashing It is not uncommon to face the following situations: u The project is behind schedule u The completion time has been moved forward Shortening the duration of the project is called project crashing © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 63

Factors to Consider When Crashing a Project u The amount by which an activity is crashed is, in fact, permissible u Taken together, the shortened activity durations will enable us to finish the project by the due date u The total cost of crashing is as small as possible © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 64

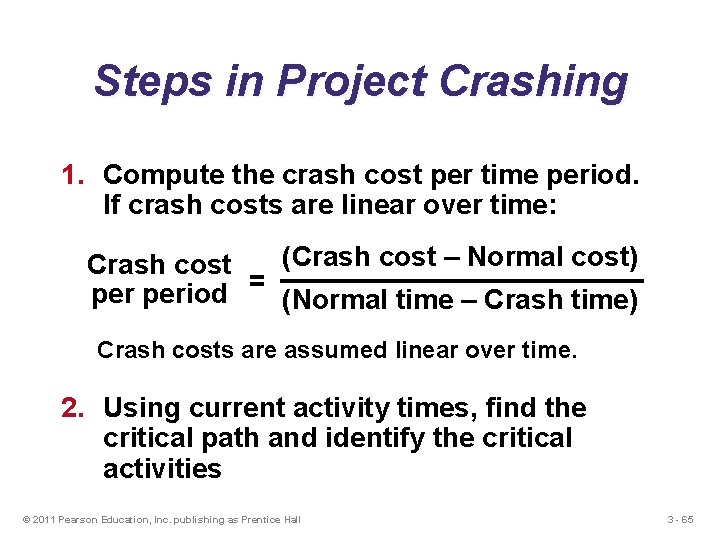
Steps in Project Crashing 1. Compute the crash cost per time period. If crash costs are linear over time: (Crash cost – Normal cost) Crash cost period = (Normal time – Crash time) Crash costs are assumed linear over time. 2. Using current activity times, find the critical path and identify the critical activities © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 65

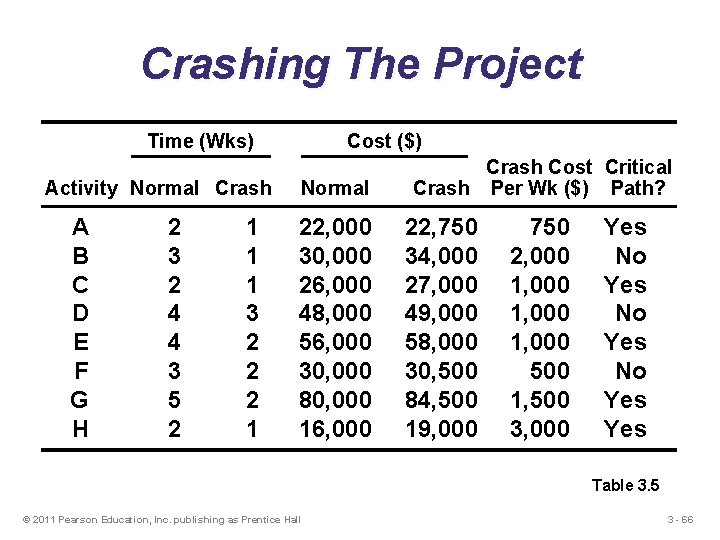
Crashing The Project Time (Wks) Activity Normal Crash A B C D E F G H 2 3 2 4 4 3 5 2 1 1 1 3 2 2 2 1 Cost ($) Normal 22, 000 30, 000 26, 000 48, 000 56, 000 30, 000 80, 000 16, 000 Crash Cost Critical Crash Per Wk ($) Path? 22, 750 34, 000 27, 000 49, 000 58, 000 30, 500 84, 500 19, 000 750 2, 000 1, 000 500 1, 500 3, 000 Yes No Yes Table 3. 5 © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 66

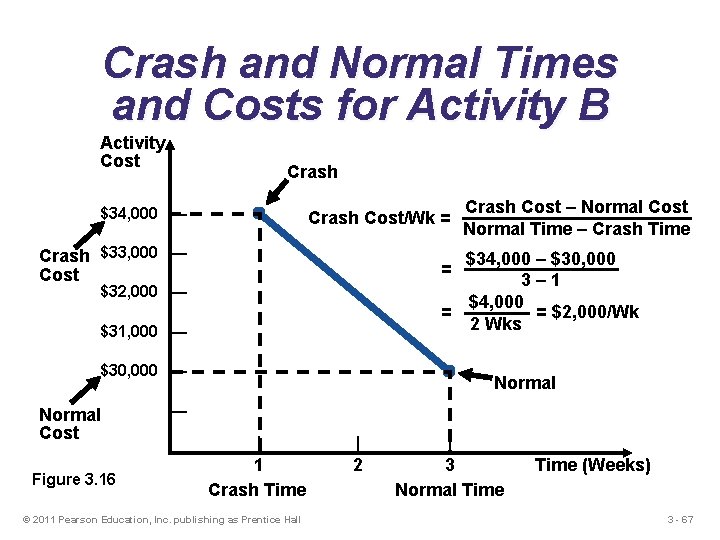
Crash and Normal Times and Costs for Activity B Activity Cost Crash $34, 000 — Crash Cost/Wk = Crash $33, 000 — Cost = $34, 000 – $30, 000 3– 1 $4, 000 = = $2, 000/Wk 2 Wks $32, 000 — $31, 000 — $30, 000 — Normal Cost Figure 3. 16 Crash Cost – Normal Cost Normal Time – Crash Time Normal — | 1 Crash Time © 2011 Pearson Education, Inc. publishing as Prentice Hall | 2 | 3 Normal Time (Weeks) 3 - 67

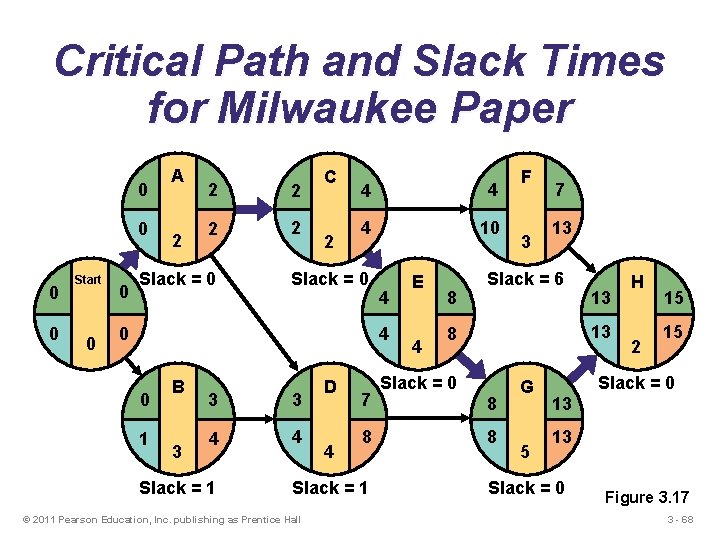
Critical Path and Slack Times for Milwaukee Paper 0 0 Start 0 0 A 2 2 2 Slack = 0 C 2 4 4 4 10 Slack = 0 0 4 4 0 1 B 3 3 3 4 4 Slack = 1 D 4 7 8 Slack = 1 © 2011 Pearson Education, Inc. publishing as Prentice Hall E 4 8 F 3 7 13 Slack = 6 13 13 8 Slack = 0 8 8 G 5 H 2 15 15 Slack = 0 13 13 Slack = 0 Figure 3. 17 3 - 68

Advantages of PERT/CPM 1. Especially useful when scheduling and controlling large projects 2. Straightforward concept and not mathematically complex 3. Graphical networks help highlight relationships among project activities 4. Critical path and slack time analyses help pinpoint activities that need to be closely watched © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 69

Advantages of PERT/CPM 5. Project documentation and graphics point out who is responsible for various activities 6. Applicable to a wide variety of projects 7. Useful in monitoring not only schedules but costs as well © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 70

Limitations of PERT/CPM 1. Project activities have to be clearly defined, independent, and stable in their relationships 2. Precedence relationships must be specified and networked together 3. Time estimates tend to be subjective and are subject to fudging by managers 4. There is an inherent danger of too much emphasis being placed on the longest, or critical, path © 2011 Pearson Education, Inc. publishing as Prentice Hall 3 - 71