3 Lie Derivatives And Lie Groups 3 1

















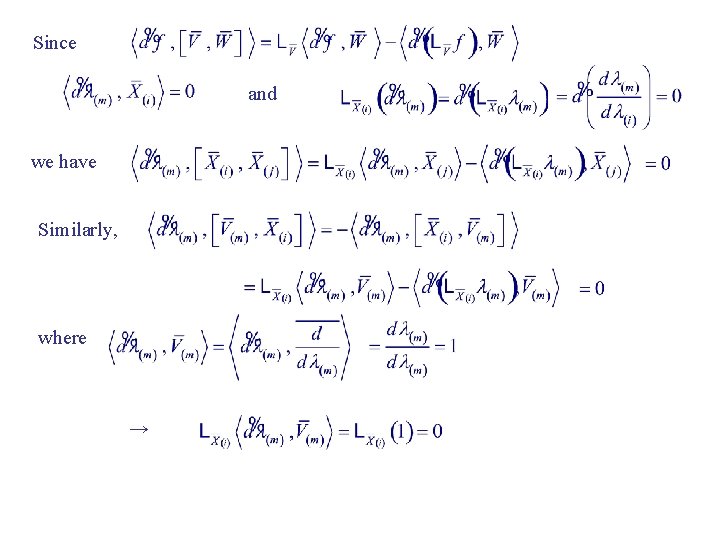














![Since if V, W are left invar fields → [ V, W ] is Since if V, W are left invar fields → [ V, W ] is](https://slidetodoc.com/presentation_image_h2/c3b988ced47386e923d9d7da16d4a889/image-36.jpg)
























- Slides: 60

3. Lie Derivatives And Lie Groups 3. 1 3. 2 3. 3 3. 4 3. 5 3. 6 3. 7 3. 8 3. 9 3. 10 3. 11 3. 12 3. 13 3. 14 3. 15 3. 16 3. 17 3. 18 Introduction: How A Vector Field Maps A Manifold Into Itself Lie Dragging A Function Lie Dragging A Vector Field Lie Derivatives Lie Derivative Of A One-form Submanifolds Frobenius' Theorem (Vector Field Version) Proof Of Frobenius' Theorem An Example: The Generators Of S 2 Invariance Killing Vector Fields Killing Vectors And Conserved Quantities In Particle Dynamics Axial Symmetry Abstract Lie Groups Examples Of Lie Groups Lie Algebras And Their Groups Realizations And Representations Spherical Symmetry, Spherical Harmonics And Representations Of The Rotation Group

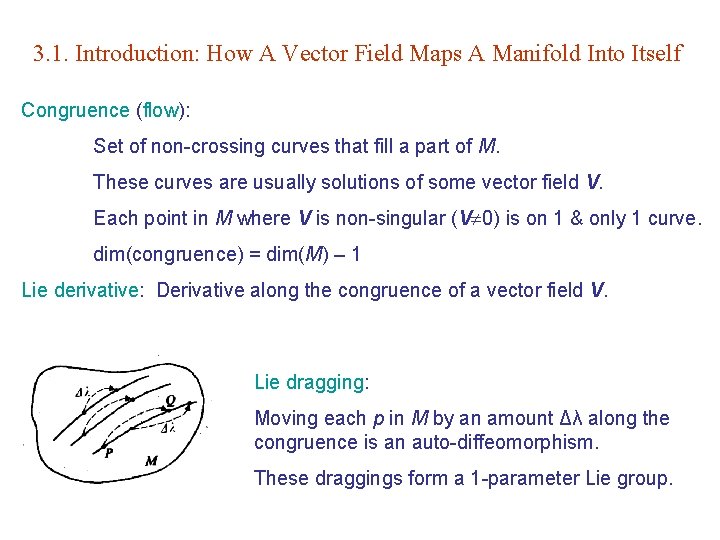
3. 1. Introduction: How A Vector Field Maps A Manifold Into Itself Congruence (flow): Set of non-crossing curves that fill a part of M. These curves are usually solutions of some vector field V. Each point in M where V is non-singular (V 0) is on 1 & only 1 curve. dim(congruence) = dim(M) – 1 Lie derivative: Derivative along the congruence of a vector field V. Lie dragging: Moving each p in M by an amount Δλ along the congruence is an auto-diffeomorphism. These draggings form a 1 -parameter Lie group.

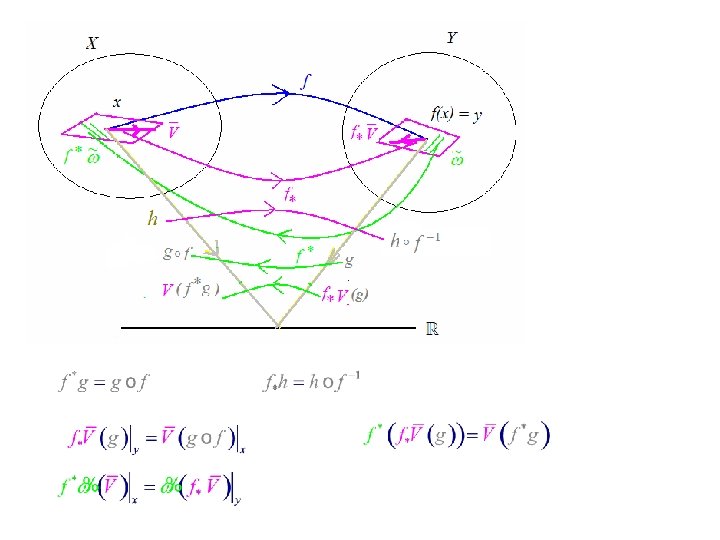
See Choquet, pp. 121 & 138. Given 1. Push-forward (differential) of f : s. t. g : Y → R, Given a coord basis: f* is also written as f , D f, or d f. 2. Pull-back (reciprocal image) of f : s. t. Given a coord basis: one can define 2 related mappings:


See Choquet, p. 144 Let σ(t, x 0) be the integral curve of i. e. , that passes through x 0 at t = 0. with since both satisfy the same differential eqs & same I. C. Define map by σt is called the local transformation generated by vector field V. (c. f. Schutz’s Lie dragging. ) → The set of all σt is a 1 -parameter transformation group. It’s local if the range of t is not all of R. In which case, it becomes a pseudo group since closure is violated.

3. 2. Lie Dragging A Function Given function f : M → R and vector field with integral curve σ(λ ) Lie-dragging f along V by Δλ gives another function s. t. i. e. fΔλ is just the push-forward : or the pull-back : f is “Lie dragged” by V if fΔλ = f.

3. 3. Given vector field Lie Dragging A Vector Field with integral curve σ(λ ) Lie dragging a vector field W along V = Operating on W by the push-forward of the local transformation.

3. 4. Lie Derivatives Lie derivative = Derivative along the congruence of a vector field. Definition: Lie derivative of a function Given function f : M → R and vector field with integral curves σ(λ, x )

Definition: Lie derivative of a vector field W along vector field V Setting where the multiplication → is defined by is not a vector field since the Leibniz rule is not obeyed. Also C 2 function f.

Properties of the Lie derivative (see Ex 3. 1 -3) ( Jacobi’s identity ) ( Leibniz rule: L is a derivation ) ( Coordinate basis ) ( General basis ) ( Coordinate-free partial )

3. 5. Lie Derivative of a 1 -form see Choquet, p. 148. Definition: Lie derivative of a 1 -form field ω along vector field V Exercise: show that c. f. ( c. f. Ex 3. 14 ) The above can also be derived from Lie derivatives of tensors can be calculated using the Leibniz rule.

d is an anti-derivation that changes a (mn) tensor into a (mn+1 ) tensor. L is a derivation that leaves the rank of a tensor unchanged. Basic formulae: ( proof: operate both sides in components on f ) Example:

3. 6. Submanifolds A submanifold S of a manifold M is a subset of M that is also a manifold. S is an s-D embedded submanifold of an m-D manifold M if there exists an atlas of M s. t. in every chart, the coordinates of S are of the form See Frankel, § 1. 3 d. or, more generally, where the y j s are functions of the xk s. Note: all solutions y to some set of equations involving x are of this form.

Consider a point p S. A curve in S through p is also a curve in M. → A (tangent) vector in Tp(S) is also a vector in Tp(M). Indeed, Tp(S) is a subspace of Tp(M). A vector in Tp(M) is not necessarily a vector in Tp(S). A 1 -form in Tp*(M) is also a 1 -form in Tp*(S) since it can map any vector in Tp(S) to R by treating it as a vector in Tp(M). A 1 -form in Tp*(S) is not necessarily a 1 -form in Tp*(M).

3. 7. Frobenius' Theorem (Vector Field Version) On a smooth manifold M, the order of partial derivatives is irrelevant. Coordinate basis vector fields commute, i. e. , since C (M) is the ring of all C functions on M. It is not a field because f 1 may not exist. The set L(M) of vector fields on M is a vector space over the field K because it is closed under linear combinations of constant coefficients. If the coefficients of linear combinations are C functions, L(M) becomes a module over the ring C (M). If L(M) is closed under the Lie bracket, it becomes a Lie algebra.

A set of vector fields are linearly independent if they are lin. indep. at each point. A set of m linearly independent, mutually commuting, vector fields can be taken as a coordinate basis using the parametrization as coordinates. By definition, their integral curves mesh to form a foliation (family of submanifolds). Each (m 1)-D submanifold, called a leaf of the foliation, is specified by a fixed value of the mth coordinate. Frobenius theorem generalize this to the case of a set of vector fields which spans a module over C (M) that is closed under the Lie bracket. Lemma : The set of all linear combinations (non-constant coefficients allowed) of a set of mutually commuting vector fields is closed under the Lie bracket. Alternative phrasing: the module over C (M) spanned by a set of mutually commuting vector fields is closed under the Lie bracket. Mathematical terms: if then Proof: See Ex 3. 5. Setting → vector fields on a submanifold are closed under the Lie bracket.

Frobenius theorem: Let L(U) be the set of all linear combinations ( with possibly non-constant coefficients ) of a set of vector fields on a region U of a manifold M. [ i. e, L(U) is a module of vector fields on U M over ring C (U). ] If L(U) is closed under the Lie bracket, then the integral curves of the vector fields mesh to form a foliation. Proof: see § 3. 8. The original version of theorem was described in terms of differential forms (see § 4. 26) and dealed with the integrability conditions of Pfaffian systems (existence of solutions of system of partial differential equations). Examples: Fig. 3. 7

3. 8 Proof of Frobenius' Theorem Ancillary relations: Strategy of proof: Since theorem is satisfied if the vector fields commute, we need only show that a set of m linearly independent, mutually commuting, vector fields can be constructed out of m lin. indep. fields that are closed under the Lie bracket. This will be done by induction. The case m = 1 is trivial since foliation = curve = leaf.

Assuming case m 1 is valid, we shall prove that case m also holds. Let the m lin. indep. fields be Let s. t. → Next, we show that and with for i = 1, … , m 1
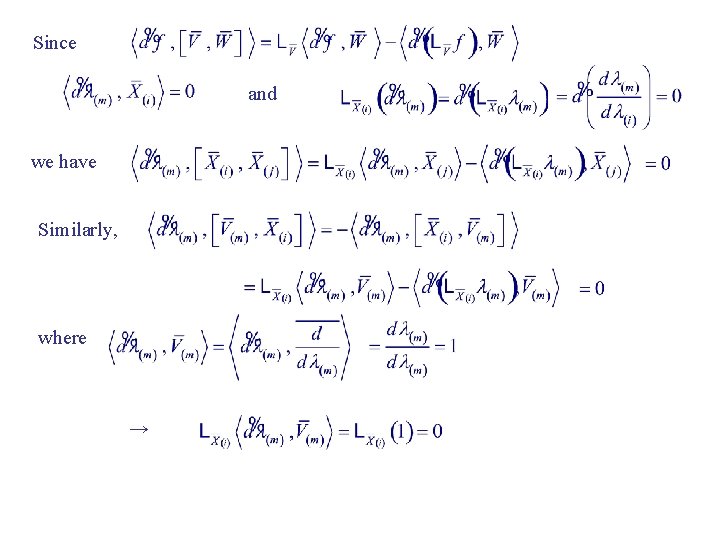
Since and we have Similarly, where →

→ → i. e. , {X(i)} is a set of m 1 lin. indep. vector fields closed under the Lie bracket. Invoking the (m 1) case of theorem, {X(i)} can be transformed into a set of m 1 of lin. indep. mutually commuting vector fields {Y(i)} whose integral curves mesh into a (m 1) D foliation S. Next, we extend {Y(i)} into the entire U by requiring it to be invariant under the group transformation generated by V(m) ( i. e. , Lie dragging along V(m) ). Calling the resultant fields {Z(i)}, this means with Since we also have QED

3. 9. An Example: The Generators of S 2 ~ In general Integral curves of ( ang mom op ) ( implied sum over repeated indices ) form a foliation with spherical leaves.

→ every li is tangent to the constant r surfaces. Only 2 of them are linearly independent at each point. Each leaf in the foliation is just S 2. Comment: Angular momenta are generators of rotations. Thus, they are antisymmetric tensors of rank 2. Only in 3 -D space are they equivalent to vectors.

3. 10. Invariance Principal use of Lie derivatives: Invariants of tensor fields → Symmetries, Lie groups … A tensor T is invariant under a vector field V if Let F = { T(1) , T(2) , … } be a set of tensor fields. Then the set A of all vector fields under which F is invariant is a Lie algebra. Proof Since : we have and i. e. , A is a vector space. From we have i. e. , A is a Lie algebra. for a R.

Caution: A is a vector space only under combinations with constant coefficients. Example: is linearly dependent in R 3. i. e. , can be satisfied with some ci (x) 0 → submanifold generated by { li } is 2 -D. However, is linearly independent if only constant ci are allowed. → Lie algebra generated by { li } is 3 -D.

3. 11. Killing Vector Fields V is a Killing vector field if the metric tensor g is invariant wrt it, i. e. , For we have & j is a Killing vector g is independent of xj E 3, Cartesian coordinates: E 3, spherical coordinates: Killing vectors: Also:

3. 12. Killing Vectors & Conserved Quantities in Particle Dynamics Classical mechanics H = T + Φ : Φ indep of x → px conserved Not so for other coordinate systems Φ indep of φ → pφ conserved Reason: Conserved momentum must be Killing vector field of configuration space. g is involved because the tensor form of the Newton’s equation is Further discussions deferred to Chapter 5.

3. 13. Axial Symmetry Axial symmetry = invariance about an axis Cylindrical symmetry = axial symmetry + translational symmetry along axis Eq of motion: L = linear operator invar under φ→ φ+ a Caution: A solution is not necessarily axially symmetric, e. g. , if is the path of a particle. Fourier analysis: → ( for a field ) m

Example: has axial eigenvalue m if If is a scalar, then → = scalar axial harmonics

Let S be the submanifold (with boundary) φ= 0. Let → Lie dragging For axis = z, S = x-z half-plane with x 0. be a 2 -D basis for TP(S) at each p S. is a basis for TP(M R 3) at p S. around the axis of symmetry generates a basis p M. Let σ(φ) be an integral curve of The basis at a point with φ= φ0 is Since we have i. e. , are all axially symmetric. Note: The Cartesian components of are functions of φ.

means have axial eigenvalues 0. are vector axial harmonics with axial eigenvalues m. i. e. , Thus, the solution to can be written as ( sum over j implied ) where a 1 , a 2 and b are independent of φ. The group of transformation (Lie draggings) { σφ } is the 1 -parameter Lie group SO(2). Spherical symmetry leads to SO(3).

3. 14. Abstract Lie Groups Choquet, pp. 116, 153. A Lie group G is a group that is also a differentiable manifold s. t. the group & differential structures are compatible. i. e is a differentiable map. , The set { σg } is a Lie group of transformations on manifold X if the map is differentiable and if the set of transformations is a group wrt composition, s. t. σe is the identity transformation with or ( Left action of G on X ) → ( Right action of G on X )

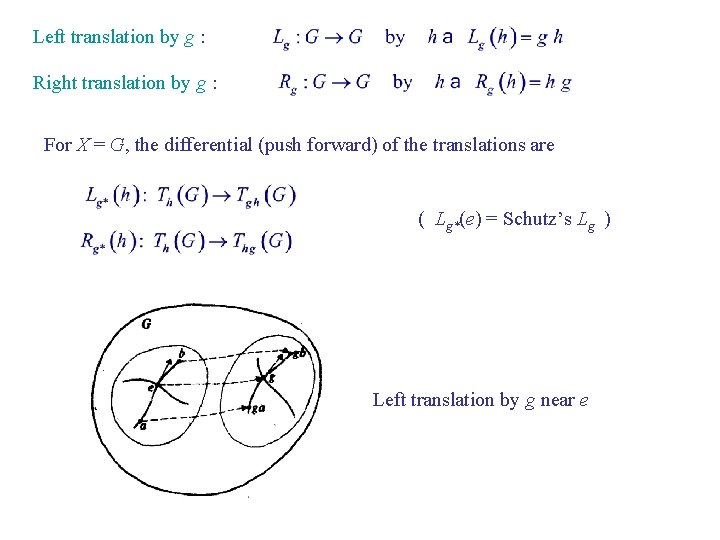
Left translation by g : Right translation by g : For X = G, the differential (push forward) of the translations are ( Lg*(e) = Schutz’s Lg ) Left translation by g near e

A vector field V on G is left invariant if it is invariant under left translations, i. e. , Note: V(h) V|h denotes the value of V at h G. Setting h = e gives where In local coordinates: For h = e : Let σ(t , g ) be the integral curve of V that passes through g for t = 0. The transformations σt = σ( t, ) form an Abelian group A with group multiplication σt σs = σt+s. Setting σ(t , e ) = g ( t ) turns the curve into a 1 -parameter Abelian subgroup of G isomorphic to A with group multiplication g(0) = e.

The subgroup { g ( t ) =σ(t , e ) } is entirely specified by It is sometimes denoted by { gγ ( t ) }. The integral curve σ(t , h ) is the left coset h { g (t ) } of { g (t ) } wrt h. By definition: → ( Exponentiation always generates a left (or right) translation along σ(t) ) For each vector γ in Te(G), one can construct a left invariant field V & hence a unique 1 -parameter subgroup { gγ ( t ) }. Every element on the path connected submanifold of G containing e belongs to one of these 1 -parameter subgroups. Restriction to invariant fields guarantees manifold: : group compatibility.
![Since if V W are left invar fields V W is Since if V, W are left invar fields → [ V, W ] is](https://slidetodoc.com/presentation_image_h2/c3b988ced47386e923d9d7da16d4a889/image-36.jpg)
Since if V, W are left invar fields → [ V, W ] is also a left-invariant field. → Left-invariant fields are closed under Lie bracket. if V, W are left invar fields → Left (or right) invariant vector fields form a vector space over R. automatically satisfied → Left (or right) invariant vector fields form a Lie algebra L(G).

Since each left invariant field is specified by its value at e, L(G) is isomorphic to G , the Lie algebra of G on Te(G). Let be a basis of G or L(G) is specified by the structual constants cki j given by is a (12) tensor. Every Lie group has a unique structure tensor but not vice versa.

3. 15. Examples of Lie Groups (i) Rn It is a manifold under the usual (n-balls) topology. It is an Abelian Lie group under vector addition. The 1 -parameter subgroups are rays ( straight lines through 0 ). The congruence of a left invariant field consists of lines parallel to a given ray. A left invariant field is therefore a constant vector field: V(x) = V(0) = γ. → All Lie brackets of left invariant fields vanish. The Lie algebra is Abelian.

(ii) GL(n, R) = Group of all n n invertible real matrices Group operation = Matrix multiplication. e = Unit matrix. g 1 = Inverse matrix. It is a differentiable manifold (Lie group) because it is a submanifold of Coordinates: n 2 matrix elements. Group manifold = Tangent space = is isomorphic to the space of all n n real matrices. 1 -parameter subgroup: where generator Other integral curves of the left-invariant vector field can be obtained by left translate (multiply) { g. A(t) } by some group element h { g. A(t) }.

Matrices with negative determinants don’t belong to any 1 -paramter subgroup. → GL(n, R) is a disconnected group. Elements path-connected to e form the component of the identity, which is just the subgroup SL(n, R). The Lie bracket of the left-invariant fields is defined as where · is the group (matrix) multiplication. the Lie bracket for the Lie algebra can be written as where A is the matrix version of the vector A|e.

(iii) O(n), SO(n) = Groups of all n n orthogonal real matrices ( S means det = +1) O(n) is disconnected. SO(n) = component of identity of O(n). A GL(n, R) can be taken as a (11) tensor on Rn. A maps a (column) vector in Rn to another vector in Rn. Similarity transform B 1 AB is a basis transformation ei → B 1 ei on A. The canonical form of A SO(n) is block diagonal with blocks of (see Ex. 3. 14) where the number of 1 blocks must be even. → Every A SO(n) represents a rotation in some 2 -D plane. SO(n) = group of rotations. The other component of O(n) represents inversions that change the handedness of basis.

Convention: Algebras of subroups of GL(n, K) are denoted by lower case letters. Let then The Lie algebra o(n) of group O(n) consists of all anti-symmetric n n matrices. The anti-symmetric condition gives n diagonal & n(n 1)/2 off-diagonal relations. → Dimensions of both o(n) & so(n) are The basis of so(3) is or so that

(iv) SU(n) = Group of all n n unitary matrices with unit determinants SU(n) is a subgroup of GL(n, C). SU(n) is the component of identity of U(n). Let then u(n) consists of all n n anti-Hermitian matrices. The anti-Hermitian condition imposes n(n 1)/2 off-diagonal complex, & n imaginary diagonal, conditions. → (Real) dimension of u(n) is The (real) dimension of group U(n) is n 2. su(n) consists of all n n anti-Hermitian traceless matrices. The (real) dimension of SU(n) is n 2 1.

3. 16. Lie Algebras & Their Groups Every Lie group G has its Lie Algebra G. Every element g of G is on one of the integral curves of a left invariant field specified by a vector in Te(G). If g is not a member of a 1 -par subgroup, the integral curve that passes through it can be obtained by a left or right translation of some subgroup. Hence, not all Lie groups can be obtained solely from their Lie algebras. Definition: Lie Algebra A Lie algebra is a vector space endowed a bilinear Lie bracket s. t. Example:

M is disconnected if 2 disjoint open sets A 1 & A 2 s. t. A 1 A 2 = M. M is connected & M are the only sets that are both open & closed. M is locally connected if every neighborhood of every point contains a connected neighborhood. ( M, π ) is a covering space of N if (see Choquet, p. 19) ① M is connected & locally connected. ② π : M → N is onto & continuous. ③ π 1 : N → M is a multi-valued homeomorphism. ④ Which means p N, neighborhood N(p) s. t. the restriction of ⑤ π to each connected component Cα of π 1 (N(p)) is a homeomorphism. Schutz’s notation: N is covered by M M is simply connected if every closed curve can be shrunk continuously to a point.

Example: R is simply connected. Example: S 1 is covered by R S 1 is multiply-connected. Sn is simply connected for n 2. Theorem: 1. Every Lie algebra is the Lie algebra of 1 & only 1 simply-connected Lie group. 2. Every Lie group with the same Lie algebra is covered by the simply-connected one.

SU(2) is simply connected Proof: Let → SU(2) = H with where H{O} is a Lie subgroup of GL(n, C) H is a 4 -D real vector space with basis Thus → SU(2) is simply connected αi R = S 3 in 4 -D α-space i. e. , every element of SU(2) can be generated by exponentiation from e

The generators Jk of a unitary matrix must be anti-hermitian. The Pauli matrix σk are hermitian → Jk i σk The Pauli matrices satisfy Setting → Note: J 2 in eq(3. 65), Schutz, is wrong. ( The structure constants should be real since the vector space & algebra are real ) A vector in Te(SU(2)) can be written as Elements of a 1 -parameter subgroup of SU(2) are given by E. g. → left invar. fields

The generators for SO(3) are (see § 3. 15): so that → E. g. n = 1, 2, …

Setting → by (SU(2) , π) is a covering space of SO(3). The domain of is t [ 0, 4 π). That of is t [ 0, 2 π). Restricting π to either t [ 0, 2 π) or t [ 2 π, 4 π) makes it a homeomorphism. → (SU(2) , π) is a double covering space of SO(3). i. e. , SO(3) is doubly covered by SU(2). The projection of S 3 onto the 3 -D space of coordinates ( α 1 , α 2 , α 3 ) is the closed ball of radius 1. ( c. f. projection of S 2 onto R 2. ) Only the outermost sphere with = 1 can be taken to represent actual points on S 3. All other spheres with r < 1 are projections. All points on a sphere have the same coordinate

Every point in the ball can be taken as e, different choices merely reflect different perspectives for the projection. Every great circle C on the r = 1 sphere is also a great circle of S 3. By choosing e to lie on the r = 1 sphere, each C on it represents a 1 parameter subgroup of SU(2). Going once around C changes t by 4π. For SO(3), each pair of diametrically opposite points on C are identical. (The pair is also diametrically opposite on S 3. ) This creates a 2 nd kind of closed path that cannot be shrunk continuously to a point : any curve joining a diametrically opposite pair of points. → SO(3) is doubly connected.

SU(2) & SO(3) share the same Lie algebra → they are identical near e. SU(2) is the only simply-connected Lie group associated with the Lie algebra. A rotation in n-D space ( an element of SO(n) ) can be represented by a vector in the Lie algebra, which is also a vector space of dimension n(n 1)/2. Thus, the association of an n-D rotation with an n-D angular momentum vector is possible only if n = n(n 1)/2, i. e. n = 3. Objects whose rotations are elements of SU(2) are called spinors. A vector in the Lie algebra ( internal space of the particle ) is called a spin. The association of a SU(2) element with a 3 -D vector allows the association of spin with an (angular momentum) vector in R 3. The Lie algebra of the Lie group Rn is an n-D Abelian Lie algebra A. Since Rn is simply-connected, all other Lie groups G with Lie algebra A must be covered by Rn. Also Rn is Abelian & identical to G near e. → G must be Abelian. All Lie groups of an Abelian algebra are Abelian.

3. 17. Realizations & Representations Abstract group : Group defined by manifold & group structure. Group in physics : symmetry transformations (operations). Realization of a group : A map T : G → L(M), where L(M) is the space of operators on M, that preserves the group structure, i. e. , The realization is a representation if L(M) is the space of linear operators on a vector space M. The realization / representation is faithful if T is 1 -1.

Example (i): The abstract group SO(3) is defined by its Lie algebra & topology. Consider the group G of all 3 3 orthogonal matrices with unit determinant. Given any column matrix x corresponding to a point x R 3 and a matrix R G, Rx represents a rotation of x. It’s straightforward to show that there is a 1 -1 correspondence of G & SO(3) that preserves the group operations. Since R 3 is a vector space, G(R 3) is a faithful representation of SO(3). The above still holds if G is applied to the 2 -sphere S 2. However, since S 2 is a manifold, G(S 2) is a faithful realization of SO(3). Historically, G(R 3) is studied first & then “abstracted” to SO(3). Most abstract groups are established in a similar manner.

Example (ii): Every group has at least 2 faithful realizations : The left- & right- translations of itself. (h → gh) is called the progressive realizations & (h → hg 1 ) the retrograde realizations. Example (iii): Adjoint Representations Given group G, the map Ig : G → G by h g h g 1 where g G is called the adjoint realization of G on G. Ig is an inner automorphism of G. The group adjoint realization need not be faithful. E. g. , Ig = id g if G is Abelian.

The differential (push-forward) Ig* of Ig at e is called the adjoint map Adg. Since g G Thus, Ig maps a 1 -par subgroup f. X (t) to another 1 -par subgroup i. e. , Taking t → 0 gives (see Ex 3. 23) See Aldrovandi, § 8. 4. → The map Ad: G → L(G, G) is called the adjoint representation of G on G. L(G, G) = space of all linear automorphisms of G. The adjoint rep is used in the definition of connection for fibre bundles.

3. 18. Spherical Symmetry, Spherical Harmonics & Representations of the Rotation Group A manifold M with metric g is spherically symmetric if the Lie algebra of its Killing vector fields has subalgebra isomorphic to so(3). Reminder: A Killing vector field generates (isometric) group of transformations. I. e. , g is invariant under translation along the integral curves of the field. The above definition avoids the possible embarassment that the “center of spherical symmetry” does not exist because it lies outside M. It was shown in § 3. 9 that the Killing vector fields on S 2 are with commutators Reminder: lj are lin. indep. under linear combinations of constant coefficients. On S 2 of radius a :

Switching to the basis gives commutators i. e. , the Lie algebra of Killing fields on S 2 the same as so(3). Conversely, a foliation in a spherically symmetric M with spherical leaves. Let L 2(S 2) be the Hilbert space of all square-integrable functions on S 2. The norm of f L 2(S 2) is defined as A realization of SO(3) on S 2 is given by the map g σg , where σg is the group of transformation σg (x) = σ( g, x ), x S 2 , g SO(3) s. t. σg h = σg σh. This induces the pull back of σg s. t.

In physics, one usually defines the function transformed by R by For the transformation Rg corresponding to σg , this means Note that Rg : L 2(S 2) → L 2(S 2) is an automorphism on linear space L 2(S 2). Hence the map R by g R(g) = Rg is a representation of SO(3) on L 2(S 2). A representation is irreducible if it contains no invariant subspaces. One task of theoretical group theory is to find all irreducible representations of a group. By definition, SO(3) has at least one faithful 3 -D representation in terms of orthogonal matrices. Since L 2(S 2) is an infinite dimensional space, the representation of SO(3) on it must be reducible. Indeed, it can be decomposed into a countable set of finite dimensional irreducible representations (IR) each specified by an integer L = 0, 1, 2, …. The Lth IR has dimension 2 L+1 and basis { YLM , M = L, L+1, …, L}.

By definition: g SO(3) where and Rg is some differential operator representing g. Historically, YLM is chosen to be the pherical harmonics, which are eigenfunctions of lz and L 2 (See Ex. 3. 24 -5 ) Since SU(2) doubly covers SO(3), the representation of SU(2) is double-valued. Thus, a faithful representation of SU(2) consists of 2 disjoint parts, each of which is a faithful representation of SO(3). IRs of SU(2) are labeled by half-integers J = 0, ½, 1, 3/2, …. Every element is on some 1 -par subgroup parametrized by t = [0, 4π) which can be splitted into 2 disjoint parts, [0, 2π) and [2π, 4π). For J = L = integers, the representation on both parts are identical. For J = odd half integers, it behaves differently.
 How are ethnic groups and religious groups related
How are ethnic groups and religious groups related Product and quotient rules and higher order derivatives
Product and quotient rules and higher order derivatives What is the principal method used to thicken tomato sauce
What is the principal method used to thicken tomato sauce Post trematic
Post trematic Hedging with forward contracts
Hedging with forward contracts Expanding logarithms
Expanding logarithms Derivative of inverse function
Derivative of inverse function Derivative of a constant
Derivative of a constant Hydrolysis of a nitrile mechanism
Hydrolysis of a nitrile mechanism Forwards vs futures vs options vs swaps
Forwards vs futures vs options vs swaps Ester and carboxylic acid
Ester and carboxylic acid How to name carboxylic acid
How to name carboxylic acid Least reactive carboxylic acid derivatives
Least reactive carboxylic acid derivatives Mother sauces definition
Mother sauces definition Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Ncert limits and derivatives pdf
Ncert limits and derivatives pdf Limits and derivatives
Limits and derivatives Derivatives and the shape of a graph
Derivatives and the shape of a graph Options futures and other derivatives
Options futures and other derivatives Is no2 para or meta directing
Is no2 para or meta directing Limits and derivatives
Limits and derivatives What are the 6 mother sauces
What are the 6 mother sauces Derivative of tan
Derivative of tan Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Lateral lingual swellings
Lateral lingual swellings Derivatives of algebraic functions
Derivatives of algebraic functions Derivative implicit
Derivative implicit Basic derivatives
Basic derivatives Stomodeum
Stomodeum Least reactive carboxylic acid derivatives
Least reactive carboxylic acid derivatives Epitheliasation
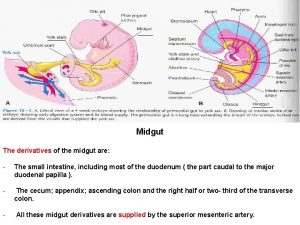
Epitheliasation Foregut midgut hindgut derivatives
Foregut midgut hindgut derivatives Find y
Find y Urushiol is a hydroxy derivative of phenol.
Urushiol is a hydroxy derivative of phenol. Samina anjum
Samina anjum Higher order derivatives meaning
Higher order derivatives meaning Prenotochordal cells
Prenotochordal cells Vitelline vein derivatives
Vitelline vein derivatives Veins
Veins Spoticash scam
Spoticash scam Blue chip derivatives
Blue chip derivatives Derivative of constant number
Derivative of constant number Warp rib weave
Warp rib weave Derivatives 2
Derivatives 2 Derivatives asset class
Derivatives asset class Derivative of inverse hyperbolic functions
Derivative of inverse hyperbolic functions Finite divided difference
Finite divided difference Acyl group
Acyl group 4th aortic arch derivatives
4th aortic arch derivatives Bilaminar
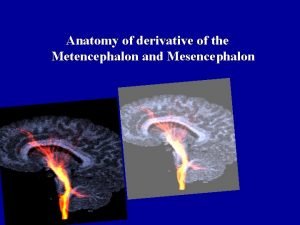
Bilaminar Metencephalon derivatives
Metencephalon derivatives How to restrict the domain
How to restrict the domain Second partial derivative formula
Second partial derivative formula Fxx fyy fxy
Fxx fyy fxy Turunan parsial orde tinggi
Turunan parsial orde tinggi Asam karboksilat dan turunannya
Asam karboksilat dan turunannya Sin tan cos derivatives
Sin tan cos derivatives How to find derivatives on ti 84
How to find derivatives on ti 84 Since
Since Derivatives of position
Derivatives of position