3 Lchantillonnage des signaux temps Cest une ncessit

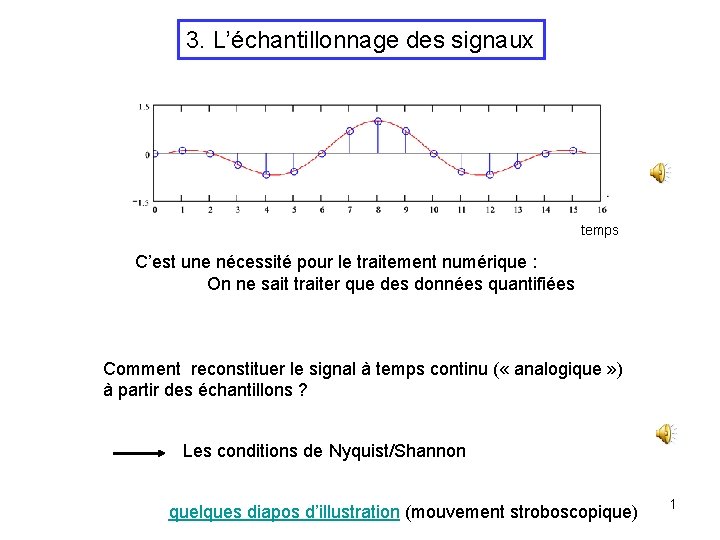
3. L’échantillonnage des signaux temps C’est une nécessité pour le traitement numérique : On ne sait traiter que des données quantifiées Comment reconstituer le signal à temps continu ( « analogique » ) à partir des échantillons ? Les conditions de Nyquist/Shannon quelques diapos d’illustration (mouvement stroboscopique) 1

illustration d’un échantillonnage insuffisamment dense en numérisation d’image sous échantillonnée : ‘moiré’ image haute définition 2 http: //en. wikipedia. org/wiki/Nyquist%E 2%80%93 Shannon_sampling_theorem

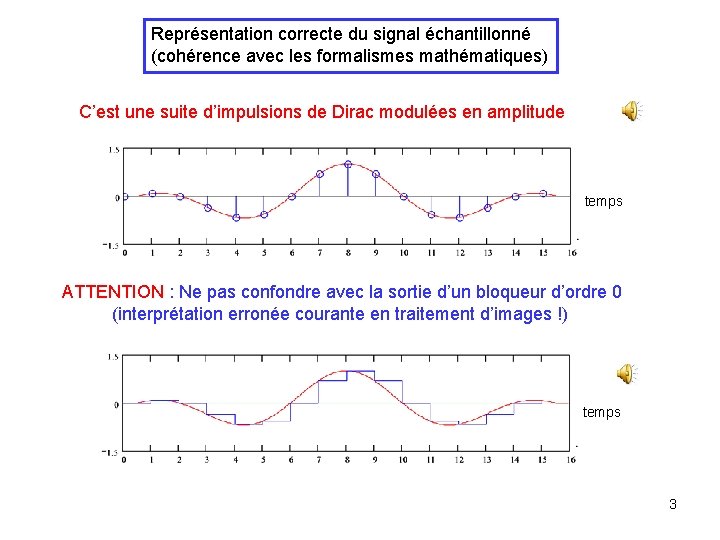
Représentation correcte du signal échantillonné (cohérence avec les formalismes mathématiques) C’est une suite d’impulsions de Dirac modulées en amplitude temps ATTENTION : Ne pas confondre avec la sortie d’un bloqueur d’ordre 0 (interprétation erronée courante en traitement d’images !) temps 3

3. 1 Interprétation de l’échantillonnage dans le domaine des fréquences - Conditions pour que l’information contenue dans le signal ne soit pas perdue : Théorème de Nyquist Shannon - Méthode de reconstruction du signal à temps continu : Interpolation idéale à partir des échantillons 4

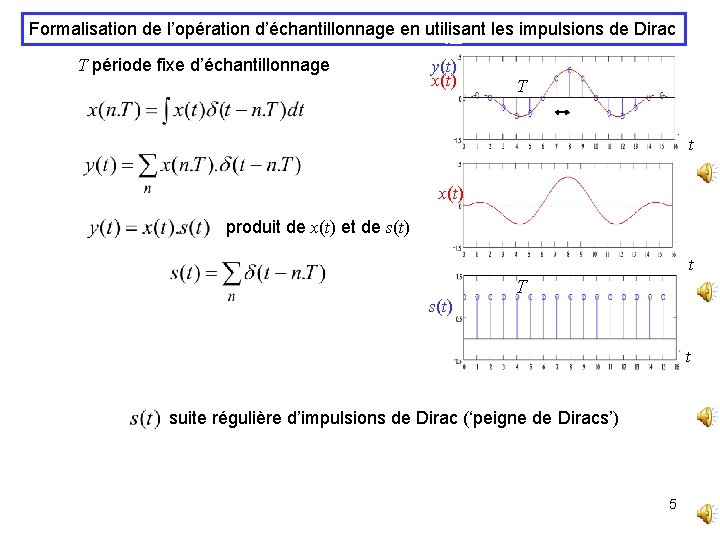
Formalisation de l’opération d’échantillonnage en utilisant les impulsions de Dirac T période fixe d’échantillonnage y(t) x(t) T t x(t) produit de x(t) et de s(t) t s(t) T t suite régulière d’impulsions de Dirac (‘peigne de Diracs’) 5

Calcul de la transformée de Fourier du peigne d’impulsions T s(t) : séquence périodique d’impulsions de Dirac (‘peigne’) ; D’après la définition de l’impulsion de Dirac, la transformée S(w) de s(t) est une fonction périodique de la fréquence : harmoniques de même amplitude aux fréquences multiples de 2 p/T t S(w) 2 p/T w 6

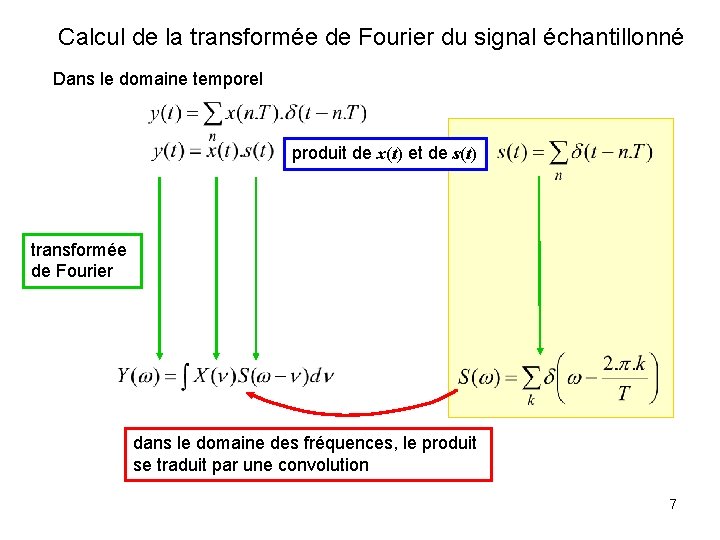
Calcul de la transformée de Fourier du signal échantillonné Dans le domaine temporel produit de x(t) et de s(t) transformée de Fourier dans le domaine des fréquences, le produit se traduit par une convolution 7

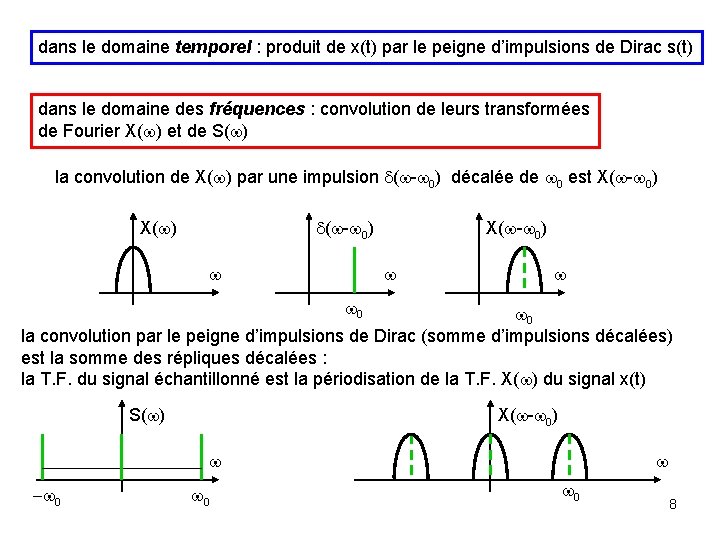
dans le domaine temporel : produit de x(t) par le peigne d’impulsions de Dirac s(t) dans le domaine des fréquences : convolution de leurs transformées de Fourier X(w) et de S(w) la convolution de X(w) par une impulsion d(w-w 0) décalée de w 0 est X(w-w 0) d(w-w 0) X(w) w X(w-w 0) w w w 0 la convolution par le peigne d’impulsions de Dirac (somme d’impulsions décalées) est la somme des répliques décalées : la T. F. du signal échantillonné est la périodisation de la T. F. X(w) du signal x(t) S(w) X(w-w 0) w -w 0 w w 0 8

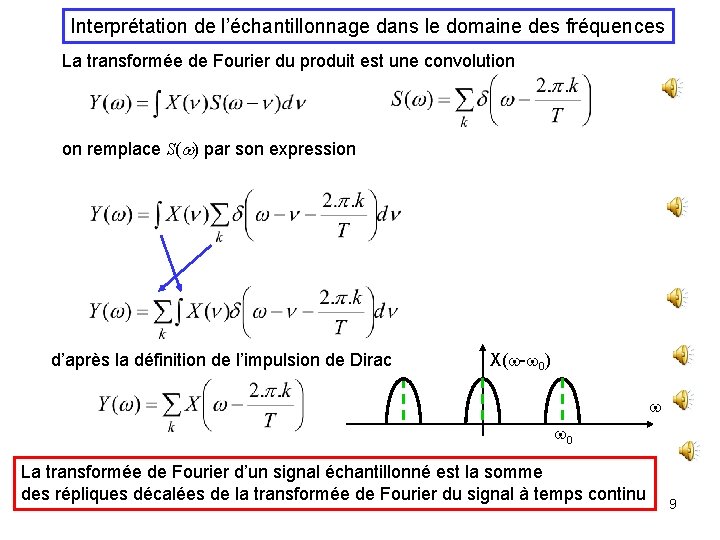
Interprétation de l’échantillonnage dans le domaine des fréquences La transformée de Fourier du produit est une convolution on remplace S(w) par son expression d’après la définition de l’impulsion de Dirac X(w-w 0) w w 0 La transformée de Fourier d’un signal échantillonné est la somme des répliques décalées de la transformée de Fourier du signal à temps continu 9

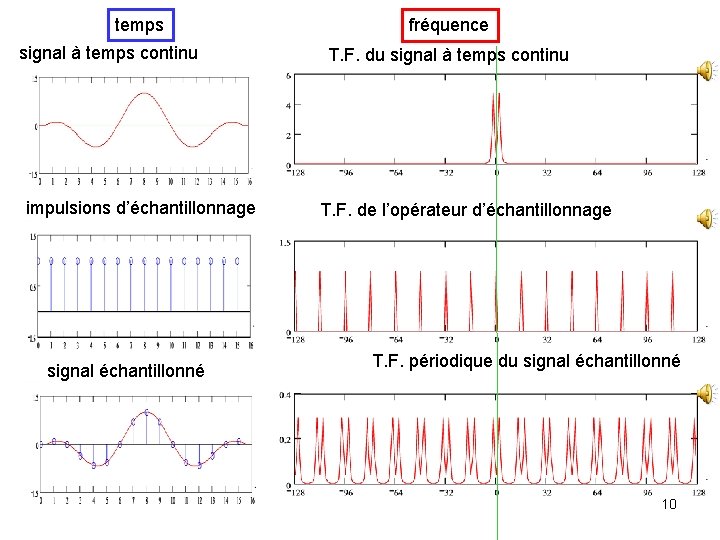
temps signal à temps continu impulsions d’échantillonnage signal échantillonné fréquence T. F. du signal à temps continu T. F. de l’opérateur d’échantillonnage T. F. périodique du signal échantillonné 10

analyse de l’échantillonnage effet stroboscopique comment observer un mouvement rapide périodique : en ne visualisant qu’une image sur N 11

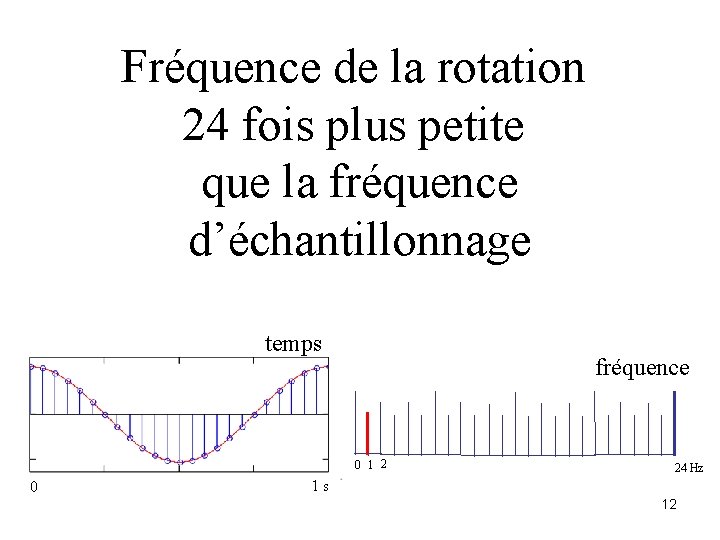
Fréquence de la rotation fréquence faible 24 fois plus petite que la fréquence d’échantillonnage temps fréquence 0 1 2 0 24 Hz 1 s 12

Mouvement à fréquence positive (convention du sens des aiguilles) 13

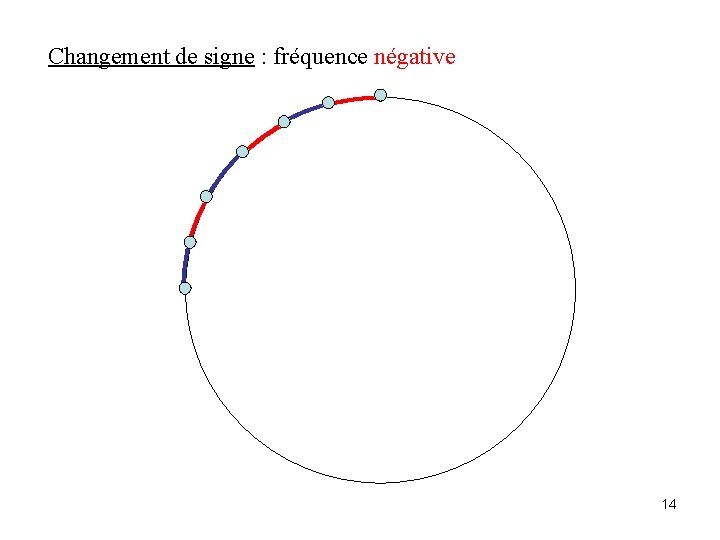
Changement de signe : fréquence négative 14

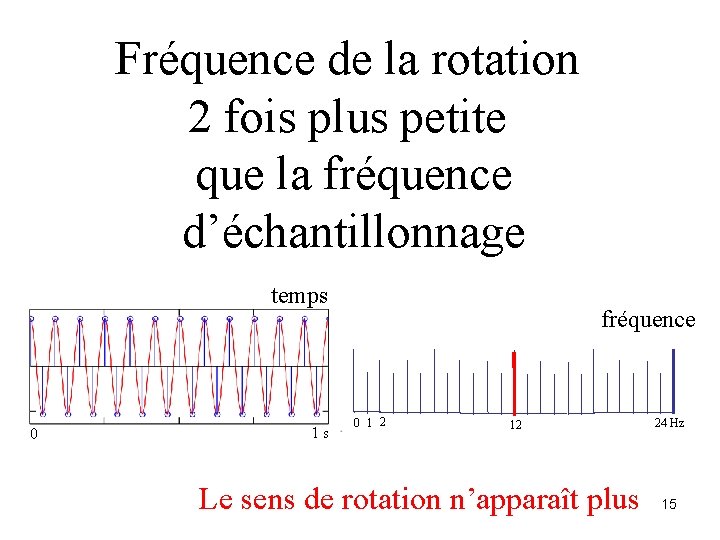
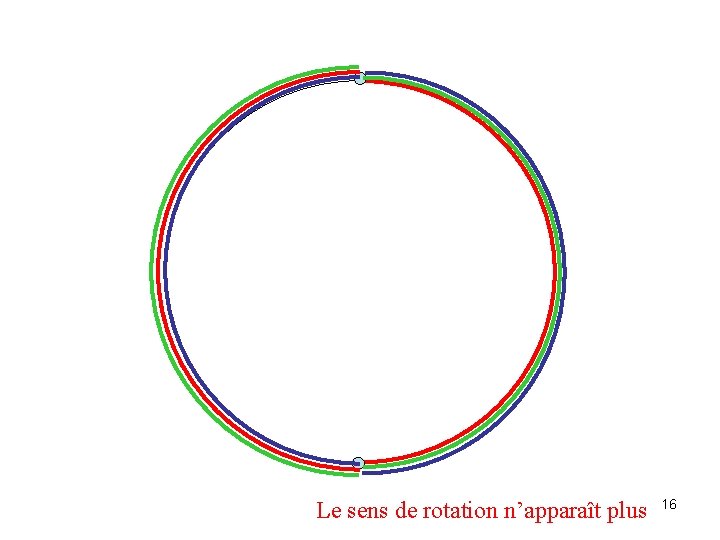
Fréquence de la rotation fréquence moitié 2 fois plus petite que la fréquence d’échantillonnage temps 0 1 s fréquence 0 1 2 12 Le sens de rotation n’apparaît plus 24 Hz 15

Le sens de rotation n’apparaît plus 16

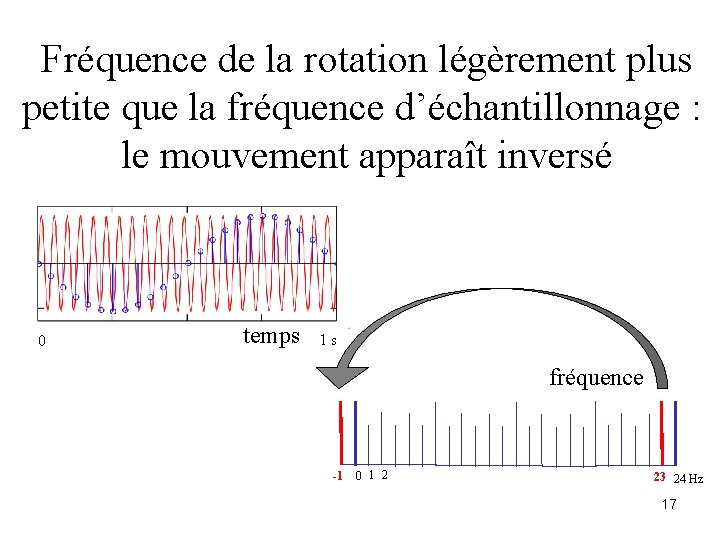
Fréquence de la rotation légèrement plus un peu en dessous de la petite que la fréquence d’échantillonnage : fréquence d ’échantillonnage le mouvement apparaît inversé 0 temps 1 s fréquence -1 0 1 2 23 24 Hz 17

Au lieu de la fréquence w, on observe la fréquence w - wech qui est négative w - wech = 23 -24 = -1 voir l’effet stroboscopique 18 cinema télévision

Effet stroboscopique : Plateau, von références Stampfer (1830) Analyse du mouvement, Chronophotographie : Muybridge, Marey (1870) Cinématographe : Edison, Lumière (1890) Consultez les différents sites qui leur Théorie de l’échantillonnage Une illustration sonore du pour les 19 http: //www. essi. fr/~leroux/listen_to_aliasing

Joseph Antoine Ferdinand Plateau Simon von Stampfer persistance rétinienne 20

Jules Janssen, astronome, 1874 Le revolver photographique Etienne Jules Marey, 1881 Eadweard J. Muybridge, 1878 Louis Aimée Augustin LE PRINCE 1888 Roundhay Garden Scene 21

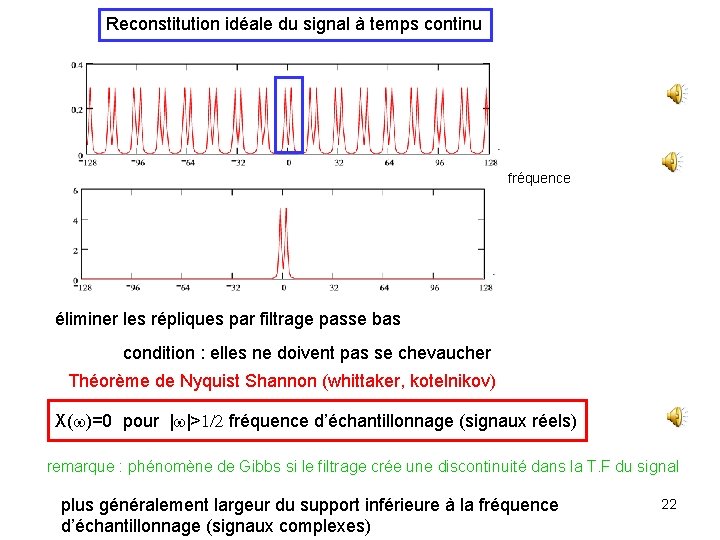
Reconstitution idéale du signal à temps continu fréquence éliminer les répliques par filtrage passe bas condition : elles ne doivent pas se chevaucher Théorème de Nyquist Shannon (whittaker, kotelnikov) X(w)=0 pour |w|>1/2 fréquence d’échantillonnage (signaux réels) remarque : phénomène de Gibbs si le filtrage crée une discontinuité dans la T. F du signal plus généralement largeur du support inférieure à la fréquence d’échantillonnage (signaux complexes) 22

transformée de Fourier du signal échantillonné X(w) w La fréquence d’échantillonnage est insuffisante les répliques de X(w) se chevauchent Y(w) wech w l’augmentation de la fréquence d’échantillonnage va supprimer ce chevauchement des répliques et permettre la reconstruction du signal à temps continu Y(w) wech w 23

réalisation du filtre passe bas dans le domaine temporel fréquence sa réponse impulsionnelle est la transformée de Fourier inverse du créneau (cas où la période ‘échantillonnage vaut 1) 24

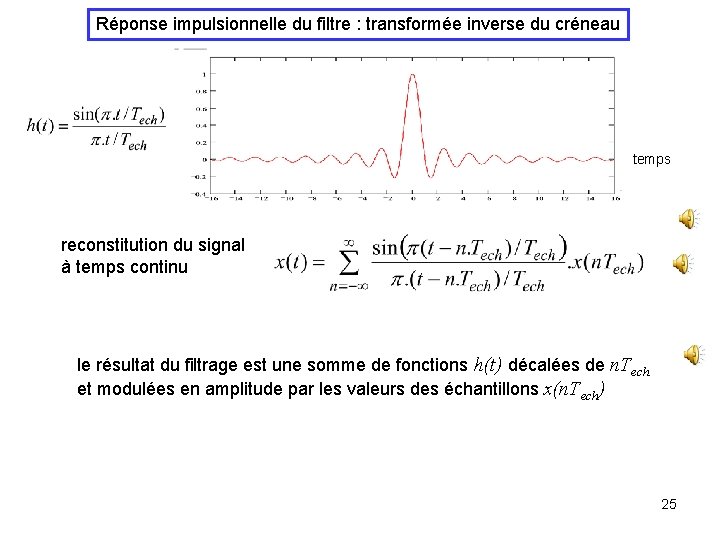
Réponse impulsionnelle du filtre : transformée inverse du créneau temps reconstitution du signal à temps continu le résultat du filtrage est une somme de fonctions h(t) décalées de n. Tech et modulées en amplitude par les valeurs des échantillons x(n. Tech) 25

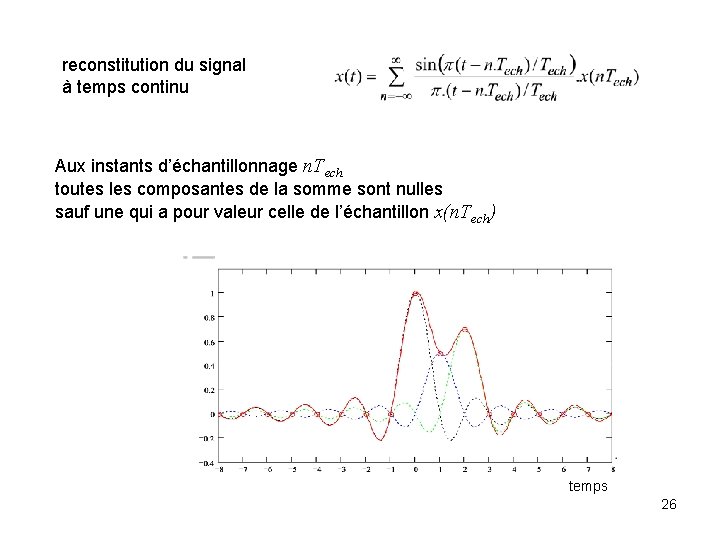
reconstitution du signal à temps continu Aux instants d’échantillonnage n. Tech toutes les composantes de la somme sont nulles sauf une qui a pour valeur celle de l’échantillon x(n. Tech) temps 26

Inconvénients : Coût, convergence lente En pratique bloqueur d’ordre zéro, interpolation linéaire interpolation plus élaborée (splines, courbes de Bézier, etc. . . ) temps 27

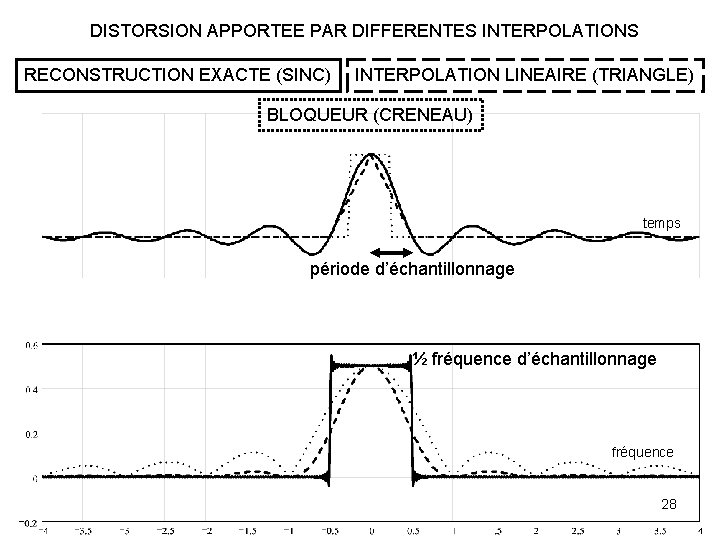
DISTORSION APPORTEE PAR DIFFERENTES INTERPOLATIONS RECONSTRUCTION EXACTE (SINC) INTERPOLATION LINEAIRE (TRIANGLE) BLOQUEUR (CRENEAU) temps période d’échantillonnage ½ fréquence d’échantillonnage fréquence 28

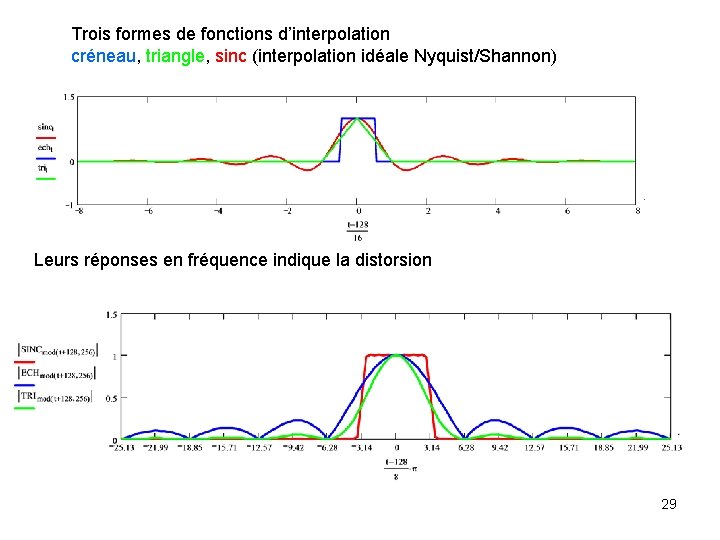
Trois formes de fonctions d’interpolation créneau, triangle, sinc (interpolation idéale Nyquist/Shannon) Leurs réponses en fréquence indique la distorsion 29

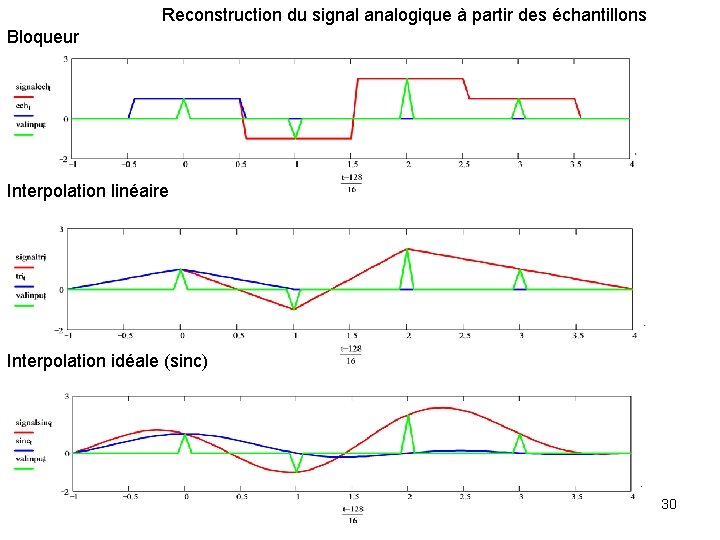
Reconstruction du signal analogique à partir des échantillons Bloqueur Interpolation linéaire Interpolation idéale (sinc) 30

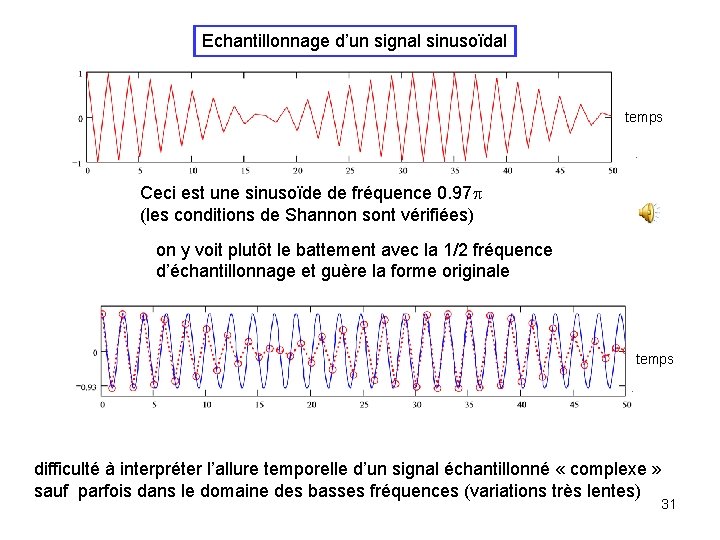
Echantillonnage d’un signal sinusoïdal temps Ceci est une sinusoïde de fréquence 0. 97 p (les conditions de Shannon sont vérifiées) on y voit plutôt le battement avec la 1/2 fréquence d’échantillonnage et guère la forme originale temps difficulté à interpréter l’allure temporelle d’un signal échantillonné « complexe » sauf parfois dans le domaine des basses fréquences (variations très lentes) 31

Quantification (p. ex. complément à 2), précision valeurs quantifiées erreur de quantification après soustraction de l’offset q 011 010 001 donnée analogique 000 111 110 101 100 écart type de l’erreur de quantification pour une précision q : 0. 29 xq 128 bits (jeux video) permettent de mesurer (en angströms =10 -10 m) le diamètre de l’univers visible (13, 7× 109 x 2 années-lumière (1, 3× 1026 m) ) 32

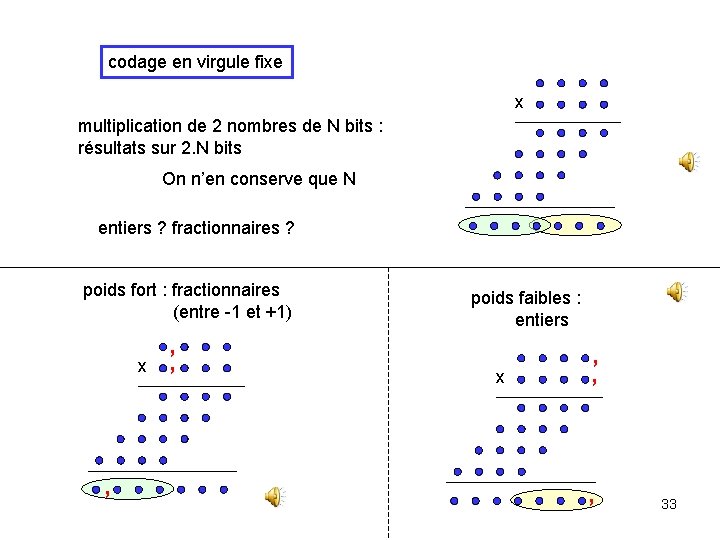
codage en virgule fixe x multiplication de 2 nombres de N bits : résultats sur 2. N bits On n’en conserve que N entiers ? fractionnaires ? poids fort : fractionnaires (entre -1 et +1) x , , , poids faibles : entiers x , , , 33

codage en « double » IEEE x=m*2 E permet d’éviter les débordements au détriment de la précision 64 bits mantisse m 53 bits (avec signe) précision 10 -15 exposant E 11 bits dynamique 10 300 attention à l’addition de deux nombres d’ordres de grandeur très différents et à la soustraction de deux nombres très proches 34