3 Forelesning Enkel Keynesmodell Lukket konomi Pensum fra

3. Forelesning Enkel Keynes-modell Lukket økonomi

Pensum fra forelesningsplanen • Keynes-modeller. Enkle regneregler som brukes for å løse Keynes-modeller • B 3, H 4 og H 5

Hva inneholder en enkel makroøkonomisk modell? • • Sentrale forutsetninger og forklaringer Ligninger Nødvendige restriksjoner på parametrene Symbolforklaring Relasjons-/ligningsforklaringer i modellen Angir endogene og eksogene variable Forklarer hvorfor noen variable er eksogene og hvorfor, for eksempel fra forhistorien, utenfor modellen eller er offentlig handlingsparameter • Determinert modellen (dvs. kontrollert at ant. endogene variable faktisk kan bestemmes i modellen)

Vi ønsker å forklare to forhold: • Virkningen på samlet produksjon (BNP) og konsum av en økning i realinvesteringene • Virkningen på samlet produksjon, konsum og samlet sparing av økt sparetilbøylighet

Enkel Keynes for lukket økonomi Sentrale forutsetninger og forklaringer: • Kort sikt • Lukket økonomi, dvs ingen utenrikshandel • Envareproduksjon • Skiller ikke mellom offentlig og privat sektor • Ledig produksjonskapasitet • Etterspørselsbestemt produksjon • Priser og lønninger er gitt • Ingen kapitaltransaksjoner • Statisk modell

Ligninger og restriksjoner Restriksjoner

Symbolforklaring • • • Y - BNP C - konsum I - investeringer c 0 – konsum c – marginal konsumtilbøylighet

Forklaringer • (1) - er en økosirk-relasjon som tar utgangspunkt i en definisjonsmessig sammenheng i nasjonalregnskapet - likevektsforutsetning, samlet produksjon (tilbud) Y tilpasser seg automatisk den samlede etterspørselen C+I. • (2) er konsumfunksjonen. - atferdsrelasjon - konsumetterspørselen er en voksende funksjon av inntekten Y - 0<c<1, er den marginale konsumtilbøylighet - c 0 > 0, inntektsuavhengig konsum

Endogene og eksogene variabler • Endogene: Y og C • Eksogene variable: I • Eksogene parametere: c 0 og c Determinere modellen: 2 ligninger & 2 endogene variable

Løsning av modellen, likevekt • Setter ligning 2 inn i 1 Y = c 0 + c. Y + I • Samler Y på en side Y-c. Y = c 0 + I (a) Løser ut for Y (b) Løser ut for C

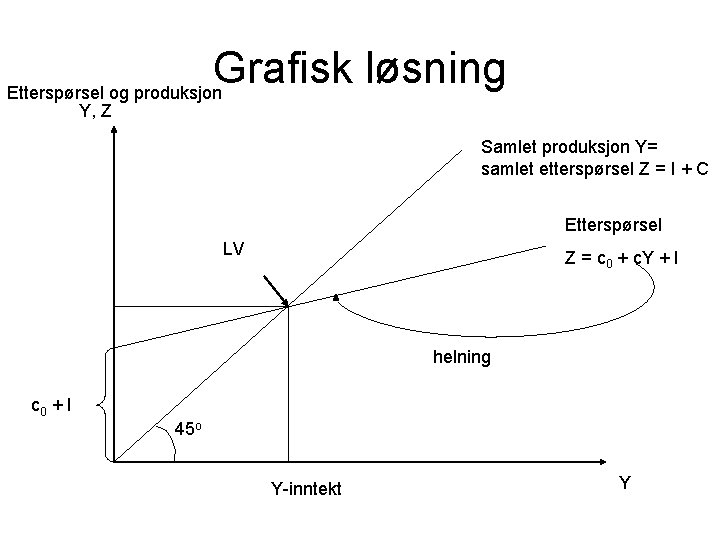
Grafisk løsning Etterspørsel og produksjon Y, Z Samlet produksjon Y= samlet etterspørsel Z = I + C Etterspørsel LV Z = c 0 + c. Y + I helning c 0 + I 45 o Y-inntekt Y

Tolkning av likevekten (LV) Fra ligningen i likevekt ser vi at: • BNP er avhengig av konsumtilbøyligheten og investeringene • Konsumet er avhenging av inntekstsuavhengig parameter, konstumtilbøyligheten og I

Endring i investeringene Beregn endring i Y og C når ΔI = I 1 – I 0 > 0 Ta utgangspunkt i LV • ΔY = Y 1 – Y 0 → • ΔC = C 1 – C 0 →

Grafisk løsning Etterspørsel og produksjon Y, Z Samlet produksjon Y= samlet etterspørsel Z = I + C Ny LV Etterspørsel Y 1 Z = c 0 + c. Y + I Y 0 c 0 + I 45 o Y 0 Y 1 Y-inntekt

Økonomisk tolkning Endring i Y • Økningen i Y er lik endringen i I multiplisert med multiplikatoren 1/(1 -c) • Økningen i Y er større enn økningen i I, kalles multiplikatoreffekten, og kommer av at konsumet øker når I øker Endring i C • C øker men mindre enn økningen i Y, siden 0<c<1 Dynamikk I↑ → etterspørsel↑ →Y↑ →inntekt til husholdning↑ → C↑ → Y↑ → inntekt til husholdning↑ → C↑ → osv…

Samme modell som tidligere, men med sparing • Vi ønsker å se hva som skjer med BNP og samlet sparing, dersom konsumentene ønsker å spare mer uansett nivå på inntekten • Vi bruker samme modell som tidligere • Legger til at privat sparing er gitt som: 3) S = Y – C som vi husker fra nasjonalregnskapet

Samme modell som tidligere, men med sparing • Vi har utledet hvordan konsumentene vil oppføre seg gjennom relasjon: 2) C= c 0+c. Y • Sett inn for C fra 2) i 3): S = Y – (c 0+c. Y) =(1 -c)Y - c 0 I følge spørsmålet skal konsumentene spare mer uavhengig inntekt og følgelig kan vi se at konsumentene sparer mer dersom c 0↓ • For å finne likevekten i modellen • Sett inn for C fra 2) i 1) her ser vi at Y bare avhenger av eksogene variable

Videre løsning av modellen • Vi kan løse modellen ved å sette inn uttrykket for Y inn i ligningen for sparing og konsum slik: • Dermed er både uttrykket for C og S bare avhengig av eksogene variable • Dermed kan vi se hvordan alle størrelser i modellen endrer seg når c 0 endrer seg, dvs. Δc 0<0

Δc 0<0 innebærer at: • Y reduseres av at konsumentene øker sparingen • Konsumet reduseres • Sparing er uendret

Tolkning av resultatene • Ser vi lettere ved å representere endring i likevekten på en annen måte

Nye uttrykk • Merk at vi kan beholde Y i uttrykkene for C og S i LV • Det kan gi en lettere tolkning av begrepene • Likevekten kan uttrykkes slik S = (1 -c)Y - c 0

Viktig å huske • I ligningen for sparing har vi to motstridende effekter – Den ene medfører at samlet sparing øker fordi Δc 0<0 – Den andre effekten kommer gjennom redusert inntekt til husholdningene dvs. Y↓ – At disse nuller ut hverandre ser vi bare gjennom å løse modellen helt

3. Forelesning Enkel Keynes-modell Med offentlig sektor Lukket økonomi

Hva inneholder en enkel makroøkonomisk modell? • • Sentrale forutsetninger og forklaringer Ligninger Nødvendige restriksjoner på parametrene Symbolforklaring Relasjons-/ligningsforklaringer i modellen Angir endogene og eksogene variable Forklarer hvorfor noen variable er eksogene og hvorfor, for eksempel fra forhistorien, utenfor modellen eller er offentlig handlingsparameter • Determinert modellen (dvs. kontrollert at ant. endogene variable faktisk kan bestemmes i modellen)

Enkel Keynes med offentlig sektor for en lukket økonomi Sentrale forutsetninger og forklaringer: • Kort sikt • Lukket økonomi, dvs ingen utenrikshandel • Envareproduksjon • Skille mellom offentlig og privat sektor • All opptjening foregår i privat sektor • Ledig produksjonskapasitet • Etterspørselsbestemt produksjon • Priser og lønninger er gitt • Ingen kapitaltransaksjoner • Statisk modell

Ligninger og restriksjoner 1) Y = C + G + I 2) C = c 0 + c(Y − T) restriksjon: 0<c<1

Symbolforklaring • Y – BNP • C – privat konsum • G – offentlig forbruk (sum av offentlig konsum og brutto realinvesteringer) • I – private brutto realinvesteringer • T – nettoskattebeløpet som det offentlige krever av det private • c 0 – inntektsuavhengig konsum • c – marginal konsumtilbøylighet

Forklaringer • (1) - er en økosirk-relasjon som tar utgangspunkt i en definisjonsmessig sammenheng i nasjonalregnskapet - likevektsforutsetning, samlet produksjon (tilbud) Y tilpasser seg automatisk den samlede etterspørselen G+C+I. • (2) er konsumfunksjonen. - atferdsrelasjon - konsumetterspørselen er en voksende funksjon av den disponible inntekten (Y-T) - 0<c<1, er den marginale konsumtilbøyelighet - c 0 > 0, inntektsuavhengig konsum

Endogene og eksogene variabler • Endogene: Y og C • Eksogene variable: I, G, T • Eksogene parametere: c 0 og c Determinere modellen: 2 ligninger & 2 endogene variable

Løsning av modellen, likevekt • Setter ligning 2 (konsumfunksjonen) inn i 1 Y = c 0 + c(Y-T) + G + I (a) Løser ut for Y Y =1/(1 − c)*(c 0 + G + I − c. T ) (b) Løser ut for C C = c 0 + c/(1 − c) * (c 0 + G + I − T) = c 0 / (1 − c) + c / (1 − c) * (G + I − T)

Tolkning av likevekten (LV) Fra ligningen i likevekt ser vi at: • BNP er avhengig av konsumtilbøyeligheten, offentlig konsum, skattene og investeringene. I og G har samme effekt på Y. • Konsumet er avhenging av inntektsuavhengige parameter, konsumtilbøyeligheten, G, T og I

Sentrale spørsmål til denne modellen • G og T er finanspolitiske virkemiddel – Er det noen forskjell om vi endrer G eller T? • Hva skjer med BNP dersom vi foretar en balansert budsjettendring?