3 Features of x Graphs The original function

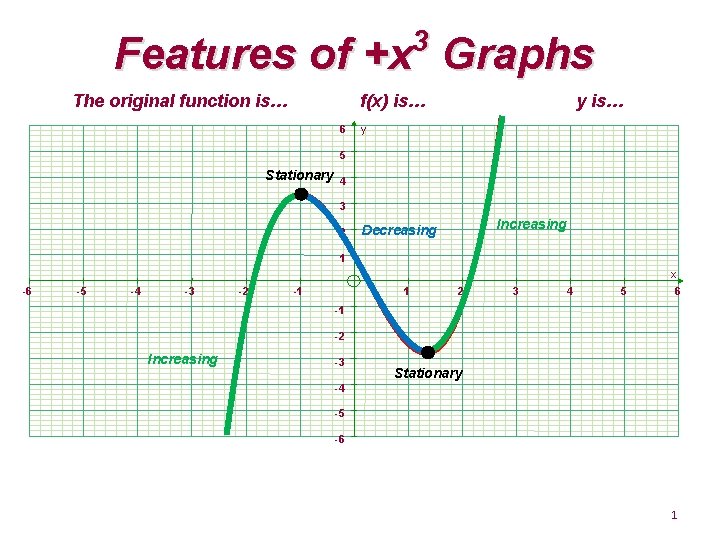
3 Features of +x Graphs The original function is… f(x) is… 6 y is… y 5 Stationary 4 3 2 Increasing Decreasing 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 Increasing -3 Stationary -4 -5 -6 1

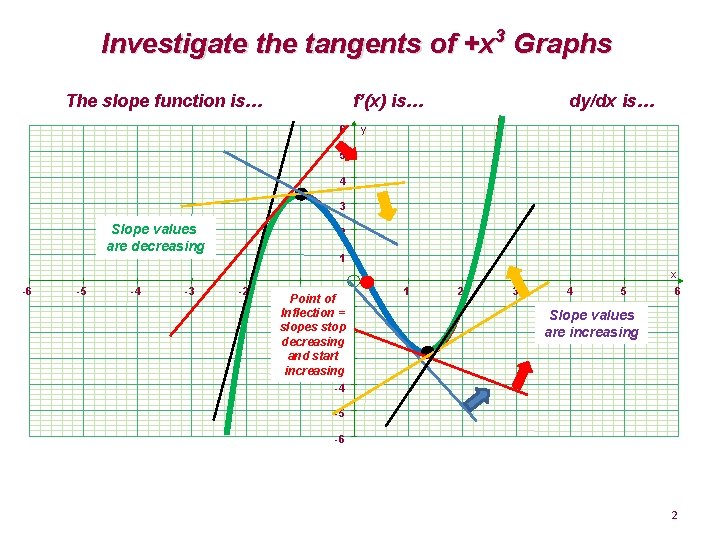
Investigate the tangents of +x 3 Graphs The slope function is… f’(x) is… 6 dy/dx is… y 5 4 3 Slope values are decreasing 2 1 x -6 -5 -4 -3 -2 -1 Point of Inflection -1 = slopes stop -2 decreasing and start-3 increasing 1 2 3 4 5 6 Slope values are increasing -4 -5 -6 2

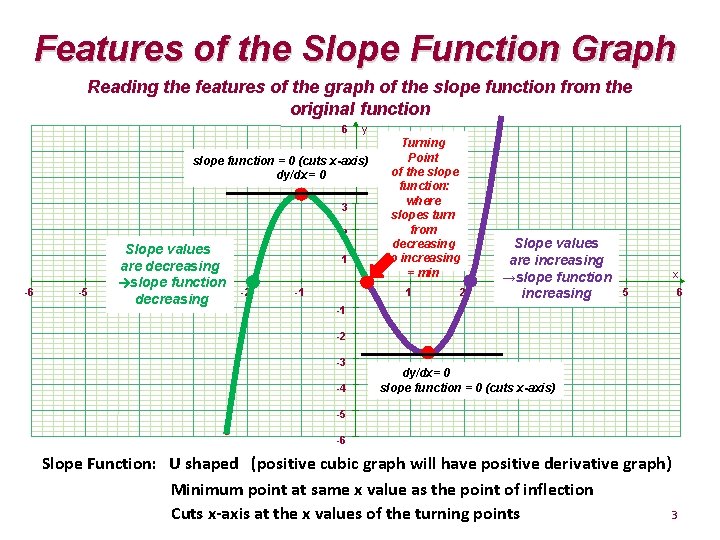
Features of the Slope Function Graph Reading the features of the graph of the slope function from the original function 6 5 y slope function = 0 (cuts x-axis) dy/dx= 0 4 3 2 -6 -5 Slope values are decreasing →slope function -4 -3 decreasing 1 -2 -1 Turning Point of the slope function: where slopes turn from decreasing to increasing = min 1 2 Slope values are increasing →slope function 3 increasing 4 x 5 6 -1 -2 -3 -4 dy/dx= 0 slope function = 0 (cuts x-axis) -5 -6 Slope Function: U shaped (positive cubic graph will have positive derivative graph) Minimum point at same x value as the point of inflection 3 Cuts x-axis at the x values of the turning points

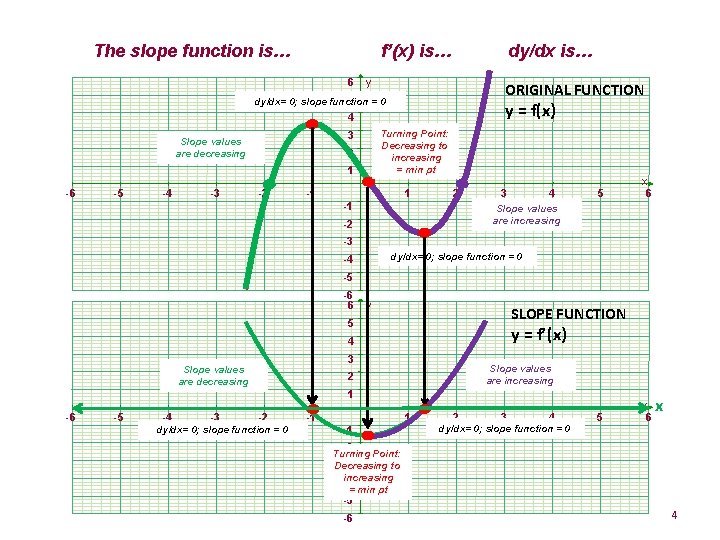
The slope function is… f’(x) is… 6 dy/dx is… y ORIGINAL FUNCTION 5 dy/dx= 0; slope function =0 y = f(x) 4 Turning Point: Decreasing to increasing = min pt 3 Slope values are decreasing 2 1 -6 -5 -4 -3 -2 -1 1 2 -1 3 4 5 x 6 Slope values are increasing -2 -3 dy/dx= 0; slope function = 0 -4 -5 -6 6 y SLOPE FUNCTION 5 y = f’(x) 4 3 Slope values are decreasing Slope values are increasing 2 1 -6 -5 -4 -3 -2 dy/dx= 0; slope function = 0 -1 1 -1 2 3 4 dy/dx= 0; slope function = 0 5 x 6 x -2 Turning Point: -3 Decreasing to increasing -4 = min pt -5 -6 4

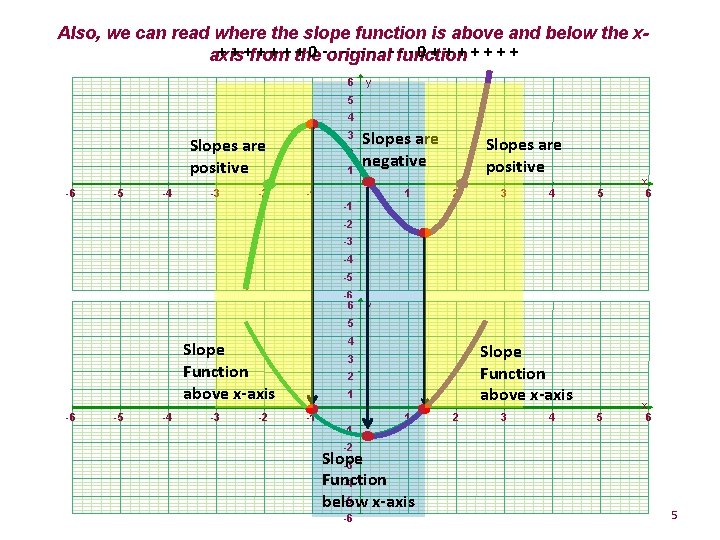
Also, we can read where the slope function is above and below the x+ + +from + + + the + 0 -original - - - - function --0+++++++ axis 6 y 5 4 3 Slopes are positive -6 -5 -4 -3 -2 2 1 Slopes are negative -1 1 Slopes are positive 2 3 4 5 x 6 -1 -2 -3 -4 -5 -6 6 y 5 4 Slope Function above x-axis -6 -5 -4 -3 -2 Slope Function above x-axis 3 2 1 -1 1 2 3 4 -1 -2 Slope -3 Function -4 -5 below x-axis -6 5

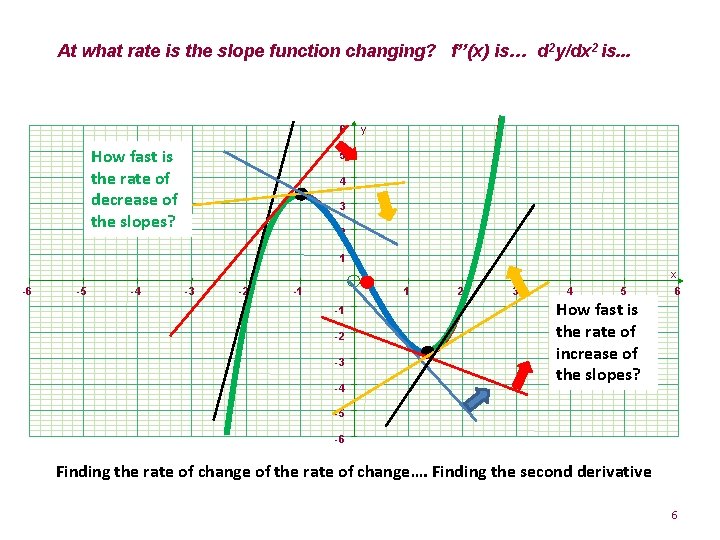
At what rate is the slope function changing? f’’(x) is… d 2 y/dx 2 is. . . 6 How fast is the rate of decrease of the slopes? y 5 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 2 3 4 5 6 How fast is the rate of increase of the slopes? -5 -6 Finding the rate of change of the rate of change…. Finding the second derivative 6

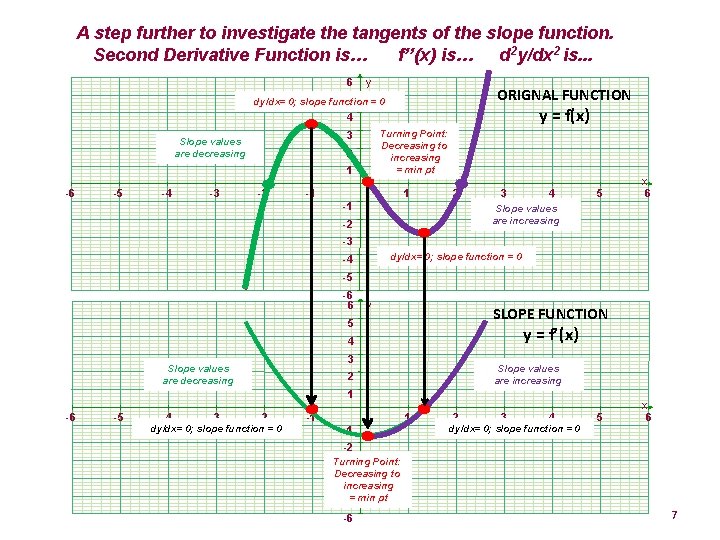
A step further to investigate the tangents of the slope function. Second Derivative Function is… f’’(x) is… d 2 y/dx 2 is. . . 6 y ORIGNAL FUNCTION 5 dy/dx= 0; slope function =0 y = f(x) 4 Turning Point: Decreasing to increasing = min pt 3 Slope values are decreasing 2 1 -6 -5 -4 -3 -2 -1 1 2 -1 3 4 5 x 6 Slope values are increasing -2 -3 dy/dx= 0; slope function = 0 -4 -5 -6 6 y SLOPE FUNCTION 5 y = f’(x) 4 3 Slope values are decreasing Slope values are increasing 2 1 -6 -5 -4 -3 -2 dy/dx= 0; slope function = 0 -1 1 -1 2 3 4 dy/dx= 0; slope function = 0 5 x 6 -2 Turning Point: -3 Decreasing to -4 increasing -5= min pt -6 7

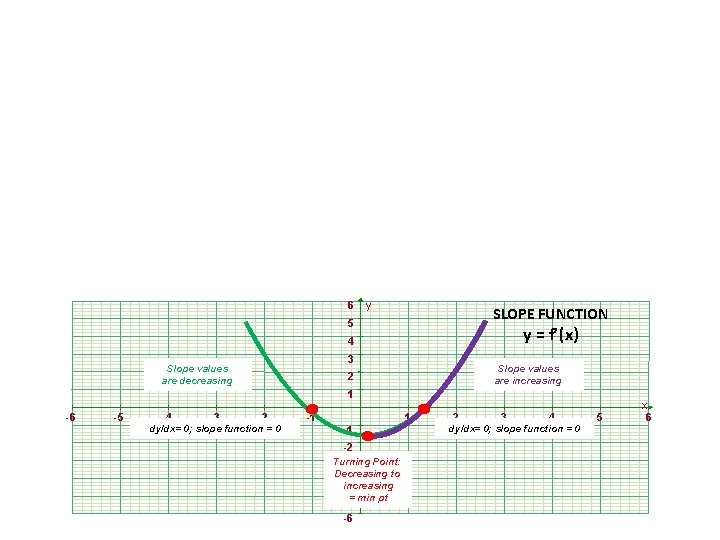
6 y SLOPE FUNCTION 5 y = f’(x) 4 3 Slope values are decreasing Slope values are increasing 2 1 -6 -5 -4 -3 -2 dy/dx= 0; slope function = 0 -1 1 -1 -2 Turning Point: -3 Decreasing to -4 increasing -5= min pt -6 2 3 4 dy/dx= 0; slope function = 0 5 x 6

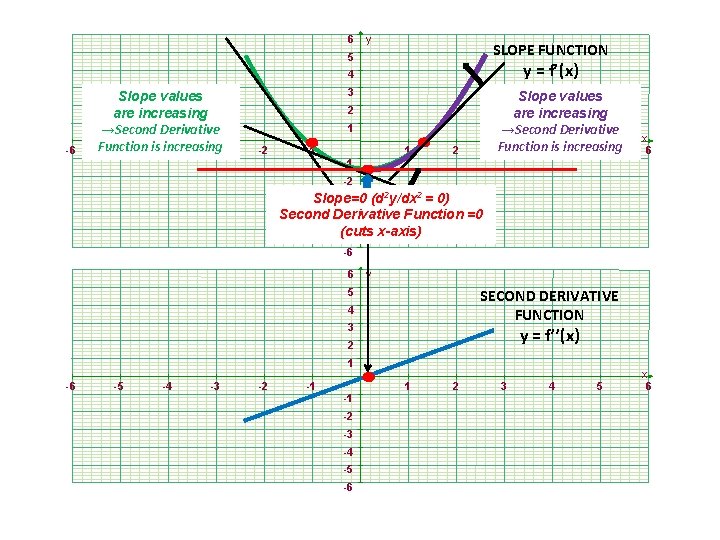
6 y SLOPE FUNCTION 5 y = f’(x) 4 -6 Slope values are increasing →Second Derivative Function is -4 increasing -5 -3 3 Slope values are increasing →Second Derivative Function 3 4 is increasing 5 2 1 -2 -1 1 2 x 6 -1 -2 -3 Slope=0 (d 2 y/dx 2 = 0) Second Derivative Function =0 -4 (cuts x-axis) -5 -6 6 y SECOND DERIVATIVE FUNCTION 5 4 3 y = f’’(x) 2 1 -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 -6 2 3 4 5 x 6

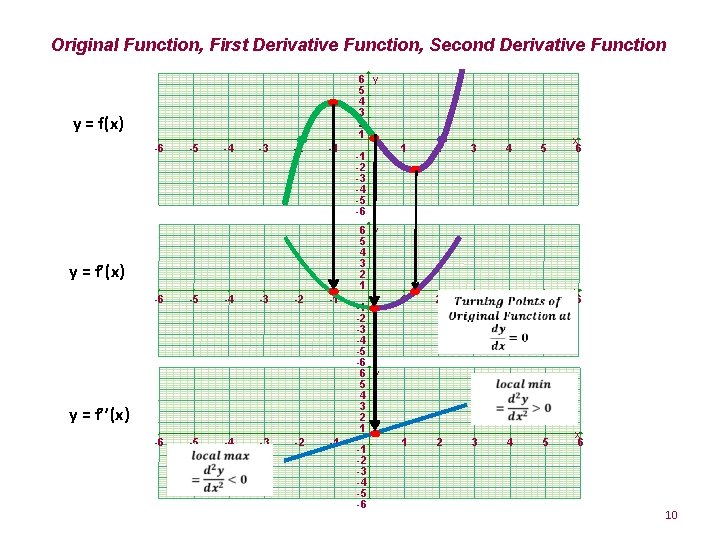
Original Function, First Derivative Function, Second Derivative Function 6 y 5 4 3 2 1 y = f(x) -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 1 2 3 4 5 x 6 6 y 5 4 3 2 1 y = f’(x) -6 -5 -4 -3 -2 -1 y = f’’(x) -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 6 y 5 4 3 2 1 -1 -2 -3 -4 -5 -6 1 2 3 10