3 Differentiation Rules Copyright Cengage Learning All rights

3 Differentiation Rules Copyright © Cengage Learning. All rights reserved.

3. 4 The Chain Rule Copyright © Cengage Learning. All rights reserved.

The Chain Rule Suppose you are asked to differentiate the function The differentiation formulas you learned in the previous sections of this chapter do not enable you to calculate F (x). Observe that F is a composite function. In fact, if we let y = f (u) = and let u = g(x) = x 2 + 1, then we can write y = F(x) = f(g (x)), that is, F = f g. We know how to differentiate both f and g, so it would be useful to have a rule that tells us how to find the derivative of F = f g in terms of the derivatives of f and g. 3

The Chain Rule It turns out that the derivative of the composite function f g is the product of the derivatives of f and g. This fact is one of the most important of the differentiation rules and is called the Chain Rule. It seems plausible if we interpret derivatives as rates of change. Regard du /dx as the rate of change of u with respect to x, dy/du as the rate of change of y with respect to u, and dy/dx as the rate of change of y with respect to x. If u changes twice as fast as x and y changes three times as fast as u, then it seems reasonable that y changes six times as fast as x, and so we expect that 4

The Chain Rule 5

The Chain Rule can be written either in the prime notation (f g) (x) = f (g(x)) g (x) or, if y = f (u) and u = g(x), in Leibniz notation: Equation 3 is easy to remember because if dy/du and du/dx were quotients, then we could cancel du. Remember, however, that du has not been defined and du /dx should not be thought of as an actual quotient. 6

Example 1 Find F '(x) if F (x) = . Solution 1: (Using Equation 2): We have expressed F as F (x) = (f g)(x) = f (g(x)) where f (u) = and g (x) = x 2 + 1. Since and g (x) = 2 x we have F (x) = f (g (x)) g (x) 7

Example 1 – Solution 2 (Using Equation 3): If we let u = x 2 + 1 and y = cont’d , then 8

The Chain Rule When using Formula 3 we should bear in mind that dy/dx refers to the derivative of y when y is considered as a function of x (called the derivative of y with respect to x), whereas dy /du refers to the derivative of y when considered as a function of u (the derivative of y with respect to u). For instance, in Example 1, y can be considered as a function of x (y = ) and also as a function of u (y = ). Note that whereas 9

The Chain Rule In general, if y = sin u, where u is a differentiable function of x, then, by the Chain Rule, Thus In a similar fashion, all of the formulas for differentiating trigonometric functions can be combined with the Chain Rule. 10

The Chain Rule Let’s make explicit the special case of the Chain Rule where the outer function f is a power function. If y = [g (x)]n, then we can write y = f(u) = un where u = g (x). By using the Chain Rule and then the Power Rule, we get 11

Example 3 Differentiate y = (x 3 – 1)100. Solution: Taking u = g(x) = x 3 – 1 and n = 100 in (4), we have = (x 3 – 1)100 = 100(x 3 – 1)99 (x 3 – 1) = 100(x 3 – 1)99 3 x 2 = 300 x 2(x 3 – 1)99 12

Exponential Functions 13

Exponential Functions Let’s try to compute the derivative of the exponential function f (x) = bx using the definition of a derivative: The factor bx doesn’t depend on h, so we can take it in front of the limit: 14

Exponential Functions Notice that the limit is the value of the derivative of f at 0, that is, Therefore we have shown that if the exponential function f (x) = bx is differentiable at 0, then it is differentiable everywhere and f (x) = f (0) bx This equation says that the rate of change of any exponential function is proportional to the function itself. (The slope is proportional to the height. ) 15

Exponential Functions Numerical evidence for the existence of f (0) is given in the table shown below for the cases b = 2 and b = 3. (Values are stated correct to four decimal places. ) It appears that the limits exist and for b = 2, for b = 3, 16

Exponential Functions In fact, it can be proved that these limits exist and, correct to six decimal places, the values are Thus, from Equation 4, we have Of all possible choices for the base b in Equation 4, the simplest differentiation formula occurs when f (0) = 1. 17

Exponential Functions In view of the estimates of f (0) for b = 2 and b = 3, it seems reasonable that there is a number b between 2 and 3 for which f (0) = 1. It is traditional to denote this value by the letter e. Thus we have the following definition. 18

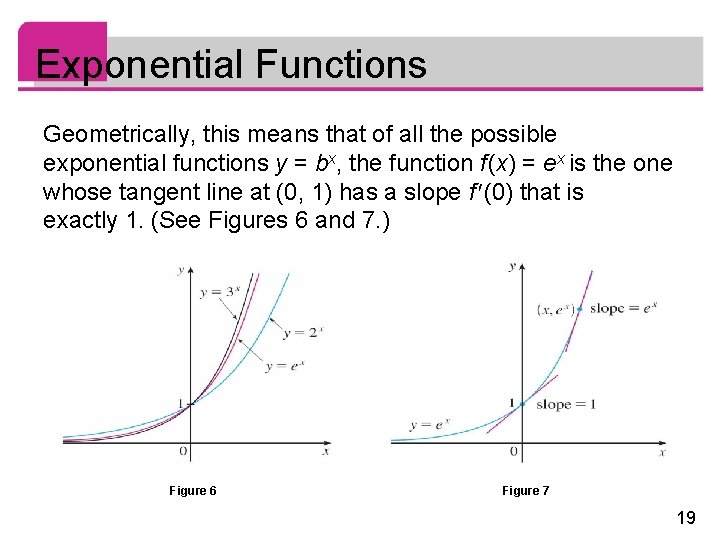
Exponential Functions Geometrically, this means that of all the possible exponential functions y = bx, the function f (x) = ex is the one whose tangent line at (0, 1) has a slope f (0) that is exactly 1. (See Figures 6 and 7. ) Figure 6 Figure 7 19

Exponential Functions If we put b = e and, therefore, f (0) = 1 in Equation 4, it becomes the following important differentiation formula. Thus the exponential function f (x) = ex has the property that it is its own derivative. The geometrical significance of this fact is that the slope of a tangent line to the curve y = ex is equal to the y-coordinate of the point (see Figure 7). 20

Example 8 If f (x) = ex – x, find f and f . Compare the graphs of f and f . Solution: Using the Difference Rule, we have 21

Example 8 – Solution cont’d We defined the second derivative as the derivative of f , so 22

The Chain Rule We can use the Chain Rule to differentiate an exponential function with any base b > 0. Recall that a = bln b. So bx = (eln b)x = e(ln b)x and the Chain Rule gives (bx) = (e(ln b)x) = e(ln b)x ln b = bx ln b because ln b is a constant. So we have the formula 23

The Chain Rule In particular, if b = 2, we get (2 x) = 2 x ln 2 We had given the estimate (2 x) (0. 69)2 x This is consistent with the exact formula (6) because ln 2 0. 693147. The reason for the name “Chain Rule” becomes clear when we make a longer chain by adding another link. 24

The Chain Rule Suppose that y = f(u), u = g(x), and x = h(t), where f, g, and h are differentiable functions. Then, to compute the derivative of y with respect to t, we use the Chain Rule twice: 25

How to Prove the Chain Rule 26

How to Prove the Chain Rule We know that if y = f(x) and x changes from a to a + x, we defined the increment of y as y = f (a + x) – f (a) According to the definition of a derivative, we have So if we denote by ε the difference between the difference quotient and the derivative, we obtain = f '(a) – f '(a) = 0 27

How to Prove the Chain Rule But y = f (a) x + ε x If we define ε to be 0 when x = 0, then ε becomes a continuous function of x. Thus, for a differentiable function f, we can write y = f (a) x + ε x where ε 0 as x 0 and ε is a continuous function of x. This property of differentiable functions is what enables us to prove the Chain Rule. 28