3 DERIVATIVES DERIVATIVES The functions that we have































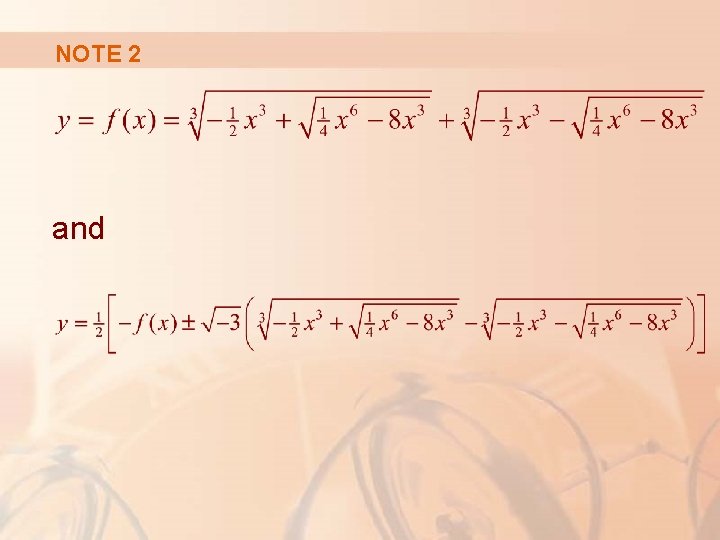







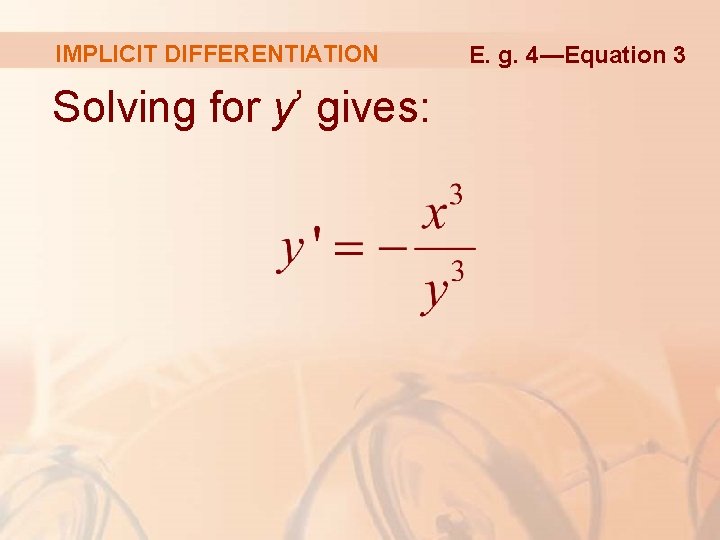



- Slides: 45

3 DERIVATIVES

DERIVATIVES The functions that we have met so far can be described by expressing one variable explicitly in terms of another variable. § For example, or in general y = f(x). , or y = x sin x,

DERIVATIVES However, some functions are defined implicitly.

DERIVATIVES 3. 6 Implicit Differentiation In this section, we will learn: How functions are defined implicitly.

IMPLICIT DIFFERENTIATION Equations 1 and 2 Some examples of implicit functions are: x 2 + y 2 = 25 x 3 + y 3 = 6 xy

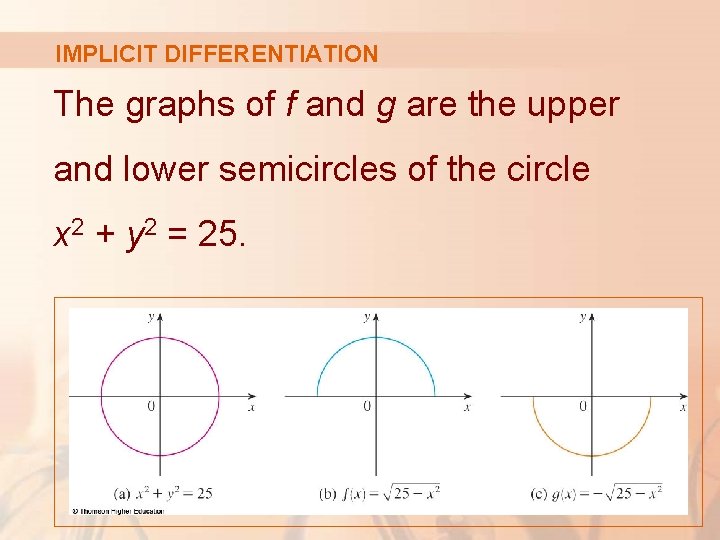
IMPLICIT DIFFERENTIATION In some cases, it is possible to solve such an equation for y as an explicit function (or several functions) of x. § For instance, if we solve Equation 1 for y, we get § So, two of the functions determined by the implicit Equation 1 are and

IMPLICIT DIFFERENTIATION The graphs of f and g are the upper and lower semicircles of the circle x 2 + y 2 = 25.

IMPLICIT DIFFERENTIATION It’s not easy to solve Equation 2 for y explicitly as a function of x by hand. § A computer algebra system has no trouble. § However, the expressions it obtains are very complicated.

FOLIUM OF DESCARTES Nonetheless, Equation 2 is the equation of a curve called the folium of Descartes shown here and it implicitly defines y as several functions of x.

FOLIUM OF DESCARTES The graphs of three functions defined by the folium of Descartes are shown.

IMPLICIT DIFFERENTIATION When we say that f is a function defined implicitly by Equation 2, we mean that the equation x 3 + [f(x)]3 = 6 x f(x) is true for all values of x in the domain of f.

IMPLICIT DIFFERENTIATION Fortunately, we don’t need to solve an equation for y in terms of x to find the derivative of y.

IMPLICIT DIFFERENTIATION METHOD Instead, we can use the method of implicit differentiation. § This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’.

IMPLICIT DIFFERENTIATION METHOD In the examples, it is always assumed that the given equation determines y implicitly as a differentiable function of x so that the method of implicit differentiation can be applied.

IMPLICIT DIFFERENTIATION a. If x 2 + y 2 = 25, find Example 1 . b. Find an equation of the tangent to the circle x 2 + y 2 = 25 at the point (3, 4).

IMPLICIT DIFFERENTIATION Example 1 a Differentiate both sides of the equation x 2 + y 2 = 25:

IMPLICIT DIFFERENTIATION Example 1 a Remembering that y is a function of x and using the Chain Rule, we have: Then, we solve this equation for :

IMPLICIT DIFFERENTIATION E. g. 1 b—Solution 1 At the point (3, 4) we have x = 3 and y = 4. So, § Thus, an equation of the tangent to the circle at (3, 4) is: y – 4 = – ¾(x – 3) or 3 x + 4 y = 25.

IMPLICIT DIFFERENTIATION E. g. 1 b—Solution 2 Solving the equation x 2 + y 2 = 25, we get: § The point (3, 4) lies on the upper semicircle § So, we consider the function

IMPLICIT DIFFERENTIATION E. g. 1 b—Solution 2 Differentiating f using the Chain Rule, we have:

IMPLICIT DIFFERENTIATION E. g. 1 b—Solution 2 So, § As in Solution 1, an equation of the tangent is 3 x + 4 y = 25.

NOTE 1 The expression dy/dx = -x/y in Solution 1 gives the derivative in terms of both x and y. It is correct no matter which function y is determined by the given equation.

NOTE 1 For instance, for , we have: However, for we have: ,

IMPLICIT DIFFERENTIATION Example 2 a. Find y’ if x 3 + y 3 = 6 xy. b. Find the tangent to the folium of Descartes x 3 + y 3 = 6 xy at the point (3, 3). c. At what points in the first quadrant is the tangent line horizontal?

IMPLICIT DIFFERENTIATION Example 2 a Differentiating both sides of x 3 + y 3 = 6 xy with respect to x, regarding y as a function of x, and using the Chain Rule on y 3 and the Product Rule on 6 xy, we get: 3 x 2 + 3 y 2 y’ = 6 xy’ + 6 y or x 2 + y 2 y’ = 2 xy’ + 2 y

IMPLICIT DIFFERENTIATION Now, we solve for y’: Example 2 a

IMPLICIT DIFFERENTIATION When x = y = 3, § A glance at the figure confirms that this is a reasonable value for the slope at (3, 3). § So, an equation of the tangent to the folium at (3, 3) is: y – 3 = – 1(x – 3) or x + y = 6. Example 2 b

IMPLICIT DIFFERENTIATION Example 2 c The tangent line is horizontal if y’ = 0. § Using the expression for y’ from (a), we see that y’ = 0 when 2 y – x 2 = 0 (provided that y 2 – 2 x ≠ 0). § Substituting y = ½x 2 in the equation of the curve, we get x 3 + (½x 2)3 = 6 x(½x 2) which simplifies to x 6 = 16 x 3.

IMPLICIT DIFFERENTIATION Example 2 c Since x ≠ 0 in the first quadrant, we have x 3 = 16. If x = 161/3 = 24/3, then y = ½(28/3) = 25/3.

IMPLICIT DIFFERENTIATION Example 2 c Thus, the tangent is horizontal at (0, 0) and at (24/3, 25/3), which is approximately (2. 5198, 3. 1748). § Looking at the figure, we see that our answer is reasonable.

NOTE 2 There is a formula for the three roots of a cubic equation that is like the quadratic formula, but much more complicated.

NOTE 2 If we use this formula (or a computer algebra system) to solve the equation x 3 + y 3 = 6 xy for y in terms of x, we get three functions determined by the following equation.
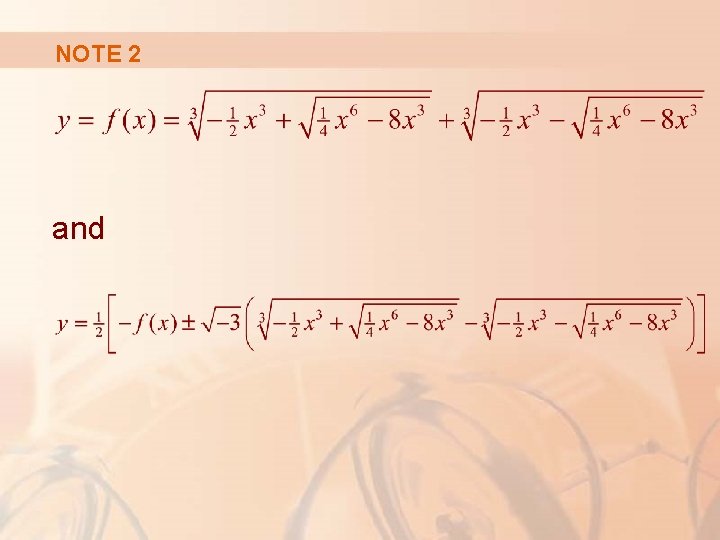
NOTE 2 and

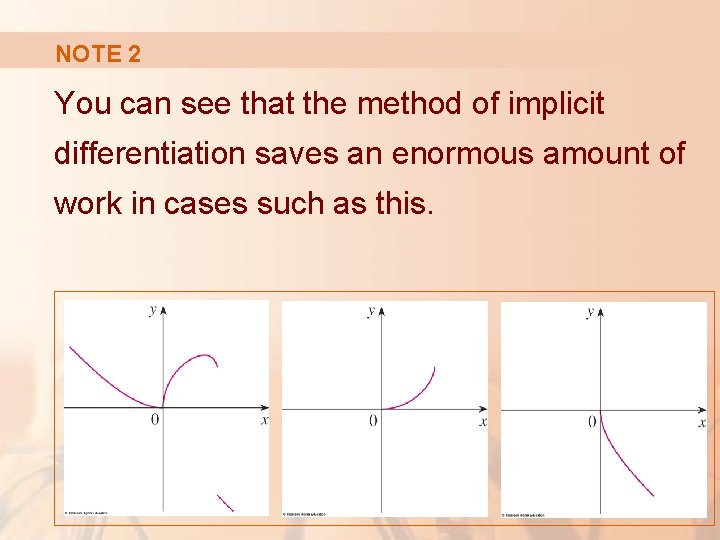
NOTE 2 These are three functions whose graphs are shown in the earlier figure.

NOTE 2 You can see that the method of implicit differentiation saves an enormous amount of work in cases such as this.

NOTE 2 Moreover, implicit differentiation works just as easily for equations such as y 5 + 3 x 2 y 2 + 5 x 4 = 12 for which it is impossible to find a similar expression for y in terms of x.

IMPLICIT DIFFERENTIATION Example 3 Find y’ if sin(x + y) = y 2 cos x. § Differentiating implicitly with respect to x and remembering that y is a function of x, we get: § Note that we have used the Chain Rule on the left side and the Product Rule and Chain Rule on the right side.

IMPLICIT DIFFERENTIATION Example 3 If we collect the terms that involve y’, we get: So,

IMPLICIT DIFFERENTIATION Example 3 The figure, drawn with the implicit-plotting command of a computer algebra system, shows part of the curve sin(x + y) = y 2 cos x. § As a check on our calculation, notice that y’ = -1 when x = y = 0 and it appears that the slope is approximately -1 at the origin.

IMPLICIT DIFFERENTIATION The following example shows how to find the second derivative of a function that is defined implicitly.

IMPLICIT DIFFERENTIATION Example 4 Find y” if x 4 + y 4 = 16. § Differentiating the equation implicitly with respect to x, we get 4 x 3 + 4 y 3 y’ = 0.
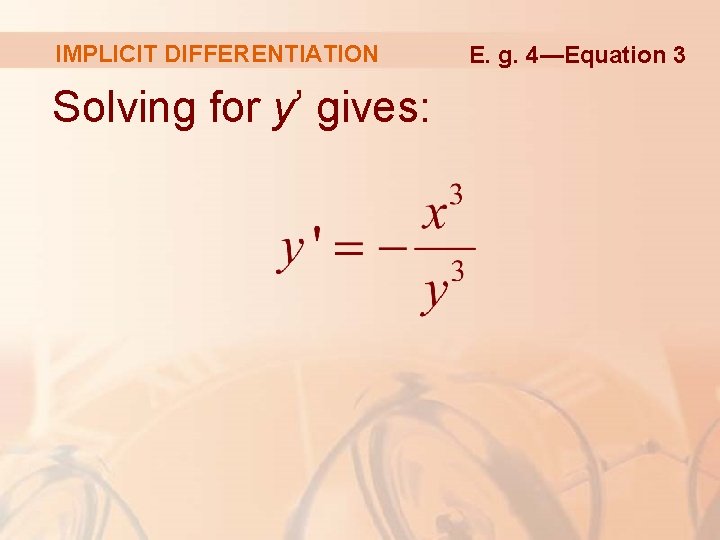
IMPLICIT DIFFERENTIATION Solving for y’ gives: E. g. 4—Equation 3

IMPLICIT DIFFERENTIATION Example 4 To find y’’, we differentiate this expression for y’ using the Quotient Rule and remembering that y is a function of x:

IMPLICIT DIFFERENTIATION Example 4 If we now substitute Equation 3 into this expression, we get:

IMPLICIT DIFFERENTIATION Example 4 However, the values of x and y must satisfy the original equation x 4 + y 4 = 16. So, the answer simplifies to:
 Ngoại tâm thu thất chùm đôi
Ngoại tâm thu thất chùm đôi Block xoang nhĩ
Block xoang nhĩ Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Chiến lược kinh doanh quốc tế của walmart
Chiến lược kinh doanh quốc tế của walmart Tìm vết của mặt phẳng
Tìm vết của mặt phẳng Hãy nói thật ít để làm được nhiều
Hãy nói thật ít để làm được nhiều Tôn thất thuyết là ai
Tôn thất thuyết là ai Gây tê cơ vuông thắt lưng
Gây tê cơ vuông thắt lưng Sau thất bại ở hồ điển triệt
Sau thất bại ở hồ điển triệt 6 equal faces 8 vertices
6 equal faces 8 vertices Differentiation formulas of trigonometric functions
Differentiation formulas of trigonometric functions Exponential differentiation
Exponential differentiation Tan inverse x
Tan inverse x Derivative of inverse hyperbolic functions
Derivative of inverse hyperbolic functions What is the inverse of ln(x)
What is the inverse of ln(x) Functions of derivatives market
Functions of derivatives market Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Frameset trong html5
Frameset trong html5 Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Chụp phim tư thế worms-breton
Chụp phim tư thế worms-breton Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính thế năng
Công thức tính thế năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Thế nào là giọng cùng tên?
Thế nào là giọng cùng tên? Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Fecboak
Fecboak Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết