3 D Geometry for Computer Graphics Class 4

3 D Geometry for Computer Graphics Class 4

The plan today n Least squares approach ¨ General / Polynomial fitting ¨ Linear systems of equations ¨ Local polynomial surface fitting 2

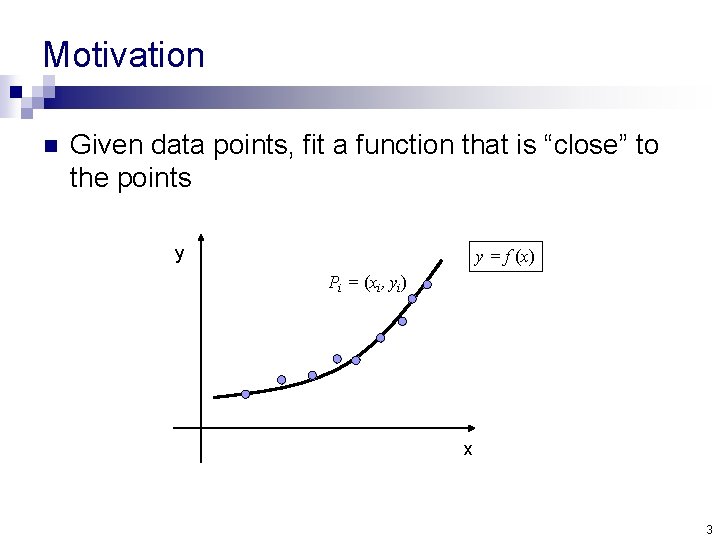
Motivation n Given data points, fit a function that is “close” to the points y y = f (x) Pi = (xi, yi) x 3

Motivation n Local surface fitting to 3 D points 4

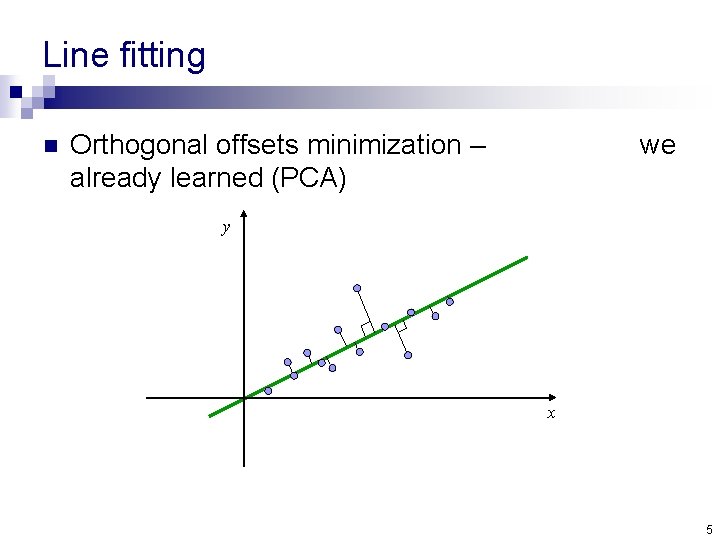
Line fitting n Orthogonal offsets minimization – already learned (PCA) we y x 5

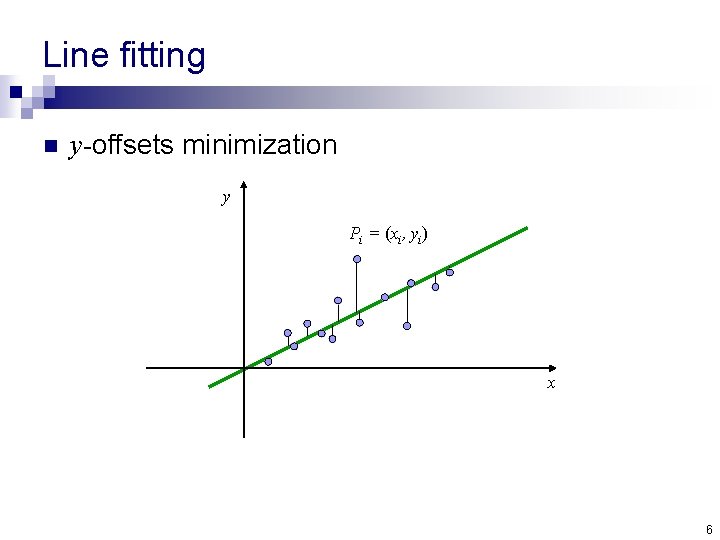
Line fitting n y-offsets minimization y Pi = (xi, yi) x 6

Line fitting n Find a line y = ax + b that minimizes n E(a, b) is quadratic in the unknown parameters a, b n Another option would be, for example: n But – it is not differentiable, harder to minimize… 7

Line fitting – LS minimization n To find optimal a, b we differentiate E(a, b): E(a, b) = (– 2 xi)[yi – (axi + b)] = 0 E(a, b) = (– 2)[yi – (axi + b)] = 0 8

Line fitting – LS minimization n We get two linear equations for a, b: (– 2 xi)[yi – (axi + b)] = 0 (– 2)[yi – (axi + b)] = 0 9

Line fitting – LS minimization n We get two linear equations for a, b: [xiyi – axi 2 – bxi] = 0 [yi – axi – b] = 0 10

Line fitting – LS minimization n We get two linear equations for a, b: ( ( x i 2) a + ( x i) b = x iy i x i) a + ( 1) b = yi 11

Line fitting – LS minimization n Solve for a, b using e. g. Gauss elimination n Question: why the solution is the minimum for the error function? E(a, b) = [yi – (axi + b)] 2 12

Fitting polynomials y x 13

Fitting polynomials n n n Decide on the degree of the polynomial, k k k-1 Want to fit f (x) = akx + ak-1 x + … + a 1 x+ a 0 Minimize: E(a 0, a 1, …, ak) = E(a 0, …, ak) = [yi – (akxik+ak-1 xik-1+ …+a 1 xi+a 0)]2 (– 2 xm)[yi – (akxik+ak-1 xik-1+…+ a 0)] = 0 14

Fitting polynomials n We get a linear system of k+1 in k+1 variables 15

General parametric fitting n We can use this approach to fit any function f(x) ¨ Specified by parameters a, b, c, … ¨ The expression f(x) linearly depends on the parameters a, b, c, … 16

General parametric fitting n Want to fit function fabc…(x) to data points (xi, yi) 2 ¨ Define E(a, b, c, …) = [yi – fabc…(xi)] ¨ Solve the linear system 17

General parametric fitting n It can even be some crazy function like n Or in general: 18

Solving linear systems in LS sense n Let’s look at the problem a little differently: ¨ We have data points (xi, yi) ¨ We want the function f(x) to go through the points: i =1, …, n: ¨ Strict n n yi = f(xi) interpolation is in general not possible In polynomials: n+1 points define a unique interpolation polynomial of degree n. So, if we have 1000 points and want a cubic polynomial, we probably won’t find it… 19

Solving linear systems in LS sense n We have an over-determined linear system n k: f(x 1) = 1 f 1(x 1) + 2 f 2(x 1) + … + k fk(x 1) = y 1 f(x 2) = 1 f 1(x 2) + 2 f 2(x 2) + … + k fk(x 2) = y 2 … … … f(xn) = 1 f 1(xn) + 2 f 2(xn) + … + k fk(xn) = yn 20

Solving linear systems in LS sense n In matrix form: 21

Solving linear systems in LS sense n In matrix form: Av = y 22

Solving linear systems in LS sense n n More constrains than variables – no exact solutions generally exist We want to find something that is an “approximate solution”: 23

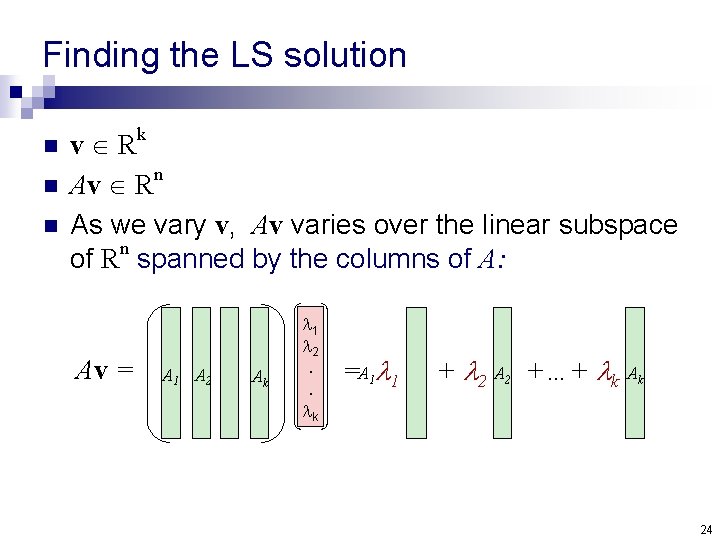
Finding the LS solution n k v R n Av R As we vary v, Av varies over the linear subspace of Rn spanned by the columns of A: Av = A 1 A 2 Ak 1 2. . k =A 1 1 + 2 A 2 +…+ k Ak 24

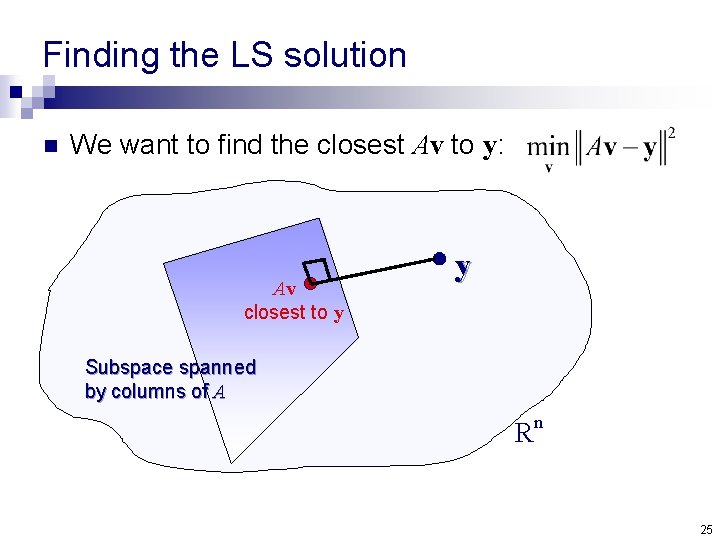
Finding the LS solution n We want to find the closest Av to y: Av closest to y y Subspace spanned by columns of A Rn 25

Finding the LS solution n The vector Av closest to y satisfies: (Av – y) {subspace of A’s columns} column Ai, <Ai, Av – y> = 0 i, Ai. T(Av – y) = 0 These are called the normal equations AT(Av – y) = 0 (ATA)v = ATy 26

Finding the LS solution n T T We got a square symmetric system (A A)v = A y (k k) n If A has full rank (the columns of A are linearly T independent) then (A A) is invertible. 27

Weighted least squares n Sometimes the problem also has weights to the constraints: 28

Local surface fitting to 3 D points n n n Normals? Lighting? Upsampling? 29

Local surface fitting to 3 D points Locally approximate a polynomial surface from points 30

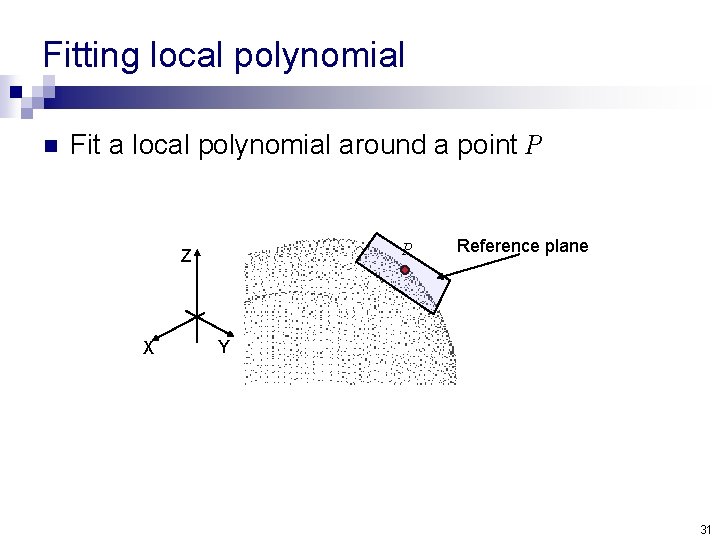
Fitting local polynomial n Fit a local polynomial around a point P P Z X Reference plane Y 31

Fitting local polynomial surface n n Compute a reference plane that fits the points close to P Use the local basis defined by the normal to the plane! z x y 32

Fitting local polynomial surface n Fit polynomial z = p(x, y) = ax 2 + bxy + cy 2 + dx + ey + f z x y 33

Fitting local polynomial surface n Fit polynomial z = p(x, y) = ax 2 + bxy + cy 2 + dx + ey + f z y x 34

Fitting local polynomial surface n Fit polynomial z = p(x, y) = ax 2 + bxy + cy 2 + dx + ey + f z x y 35

Fitting local polynomial surface n Again, solve the system in LS sense: ax 12 + bx 1 y 1 + cy 12 + dx 1 + ey 1 + f = z 1 ax 22 + bx 2 y 2 + cy 22 + dx 2 + ey 2 + f = z 1. . . axn 2 + bxnyn + cyn 2 + dxn + eyn + f = zn n Minimize ||zi – p(xi, yi)||2 36

Fitting local polynomial surface n Also possible (and better) to add weights: wi ||zi – p(xi, yi)||2, wi > 0 n The weights get smaller as the distance from the origin point grows. 37

See you next time