3 D Geometry for Computer Graphics Class 1

3 D Geometry for Computer Graphics Class 1

General n Office hour: Sunday 11: 00 – 12: 00 in Schreiber 002 (contact in advance) n Webpage with the slides: http: //www. cs. tau. ac. il/~sorkine/courses/cg/cg 2005/ n E-mail: sorkine@tau. ac. il

The plan today n n Basic linear algebra and Analytical geometry

Why? ?

Why? ? n We represent objects using mainly linear primitives: points ¨ lines, segments ¨ planes, polygons ¨ n Need to know how to compute distances, transformations, projections…

Basic definitions n n Points specify location in space (or in the plane). Vectors have magnitude and direction (like velocity). Points Vectors

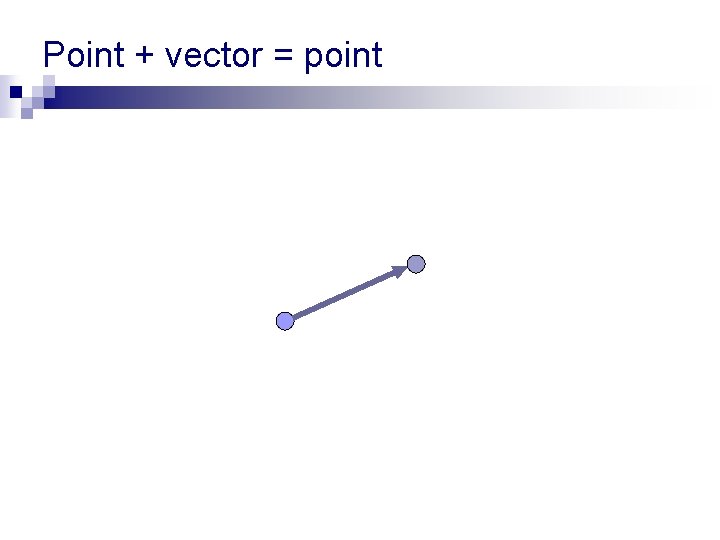
Point + vector = point

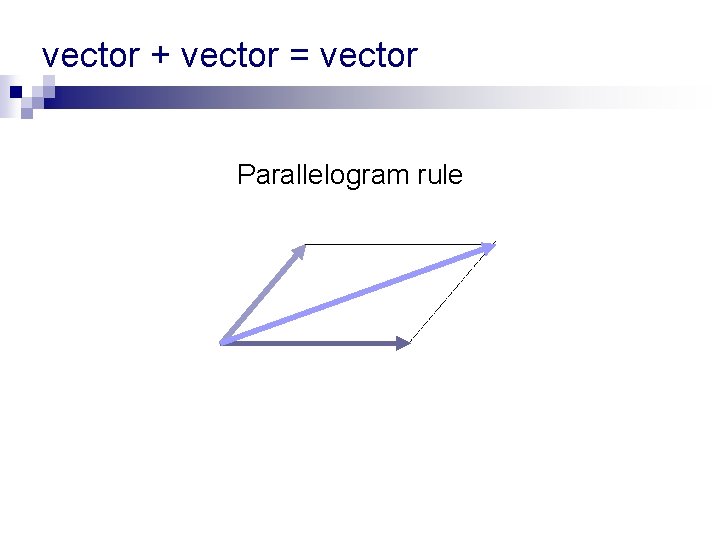
vector + vector = vector Parallelogram rule

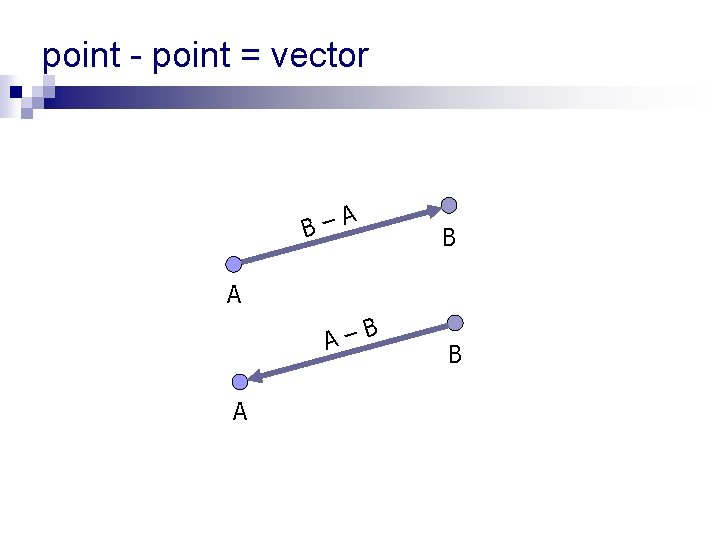
point - point = vector B– A B A A– A B B

point + point: not defined!!

Map points to vectors n n If we have a coordinate system with origin at point O We can define correspondence between points and vectors:

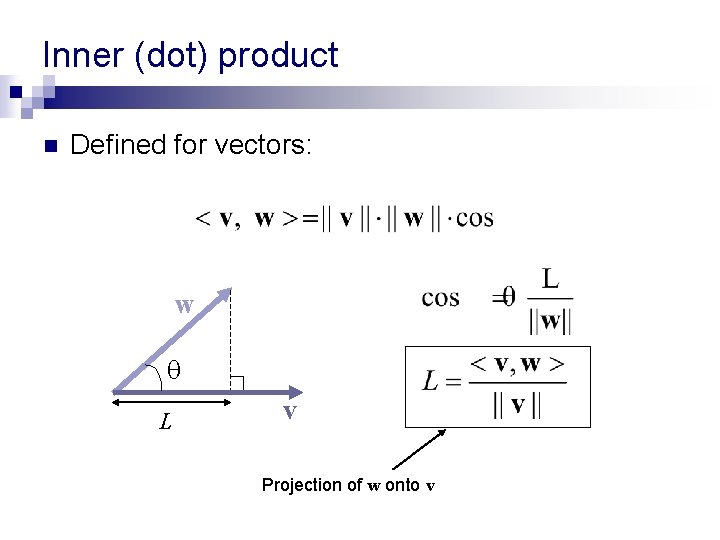
Inner (dot) product n Defined for vectors: w L v Projection of w onto v

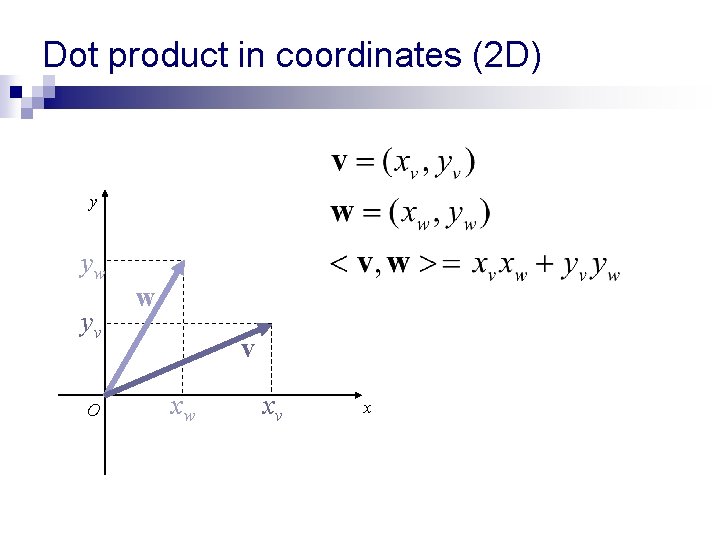
Dot product in coordinates (2 D) y yw yv O w v xw xv x

Perpendicular vectors (2 D) v v

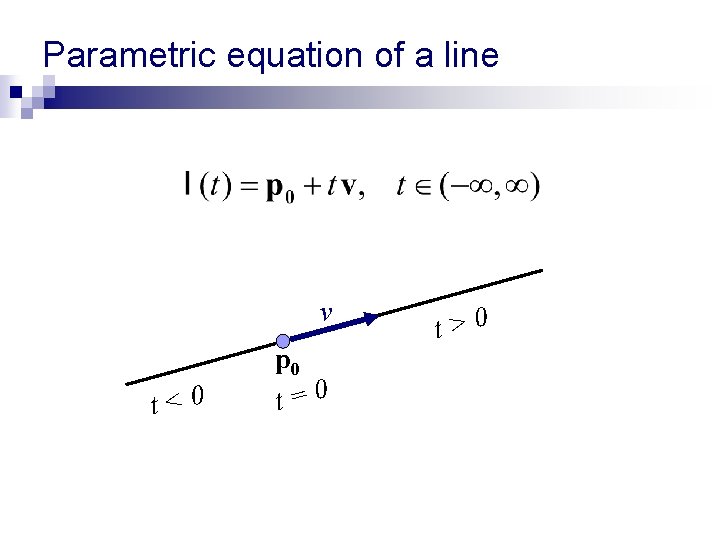
Parametric equation of a line v t<0 p 0 t=0 t>0

Parametric equation of a ray v p 0 t=0 t>0

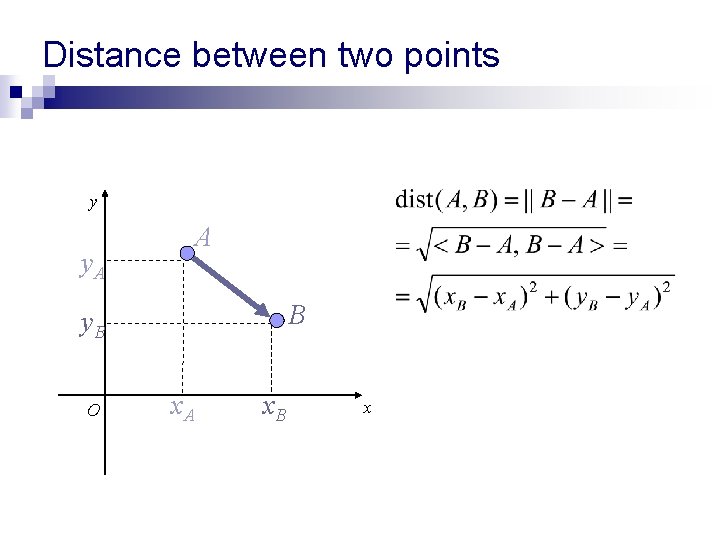
Distance between two points y y. A A B y. B O x. A x. B x

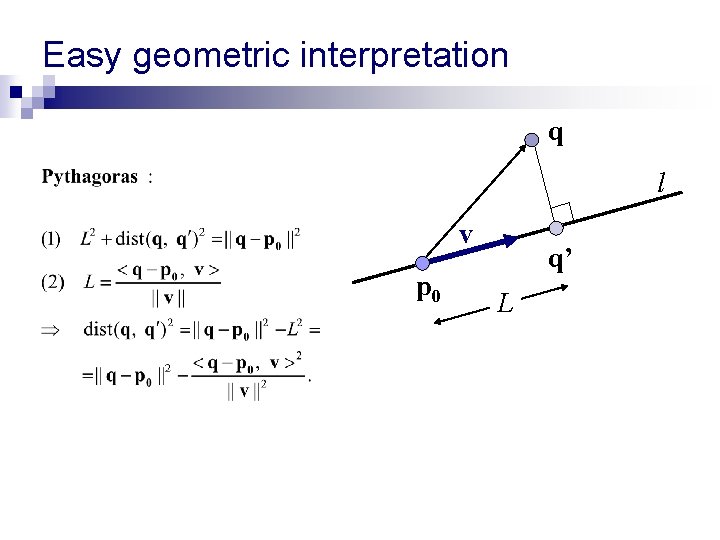
Distance between point and line q Find a point q’ such that (q q’) v dist(q, l) = || q q’ || l v p 0 q’ = p 0 +tv

Easy geometric interpretation q l v p 0 q’ L

Distance between point and line – also works in 3 D! n n The parametric representation of the line is coordinates-independent v and p 0 and the checked point q can be in 2 D or in 3 D or in any dimension…

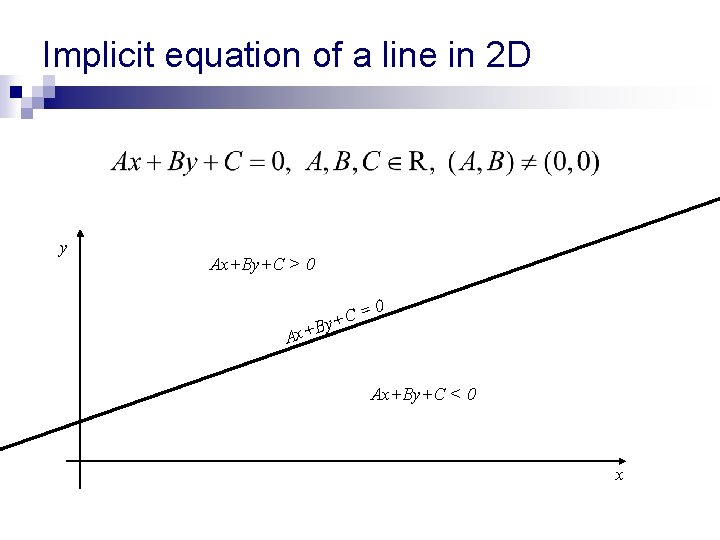
Implicit equation of a line in 2 D y Ax+By+C > 0 Ax+ C By+ =0 Ax+By+C < 0 x

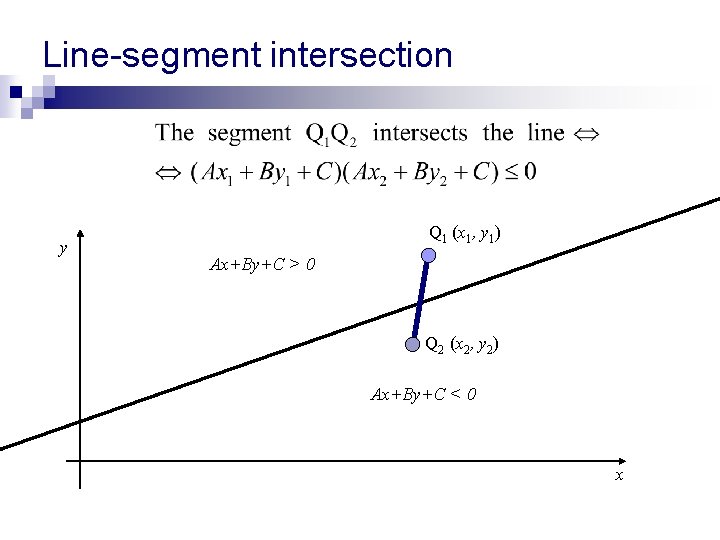
Line-segment intersection y Q 1 (x 1, y 1) Ax+By+C > 0 Q 2 (x 2, y 2) Ax+By+C < 0 x

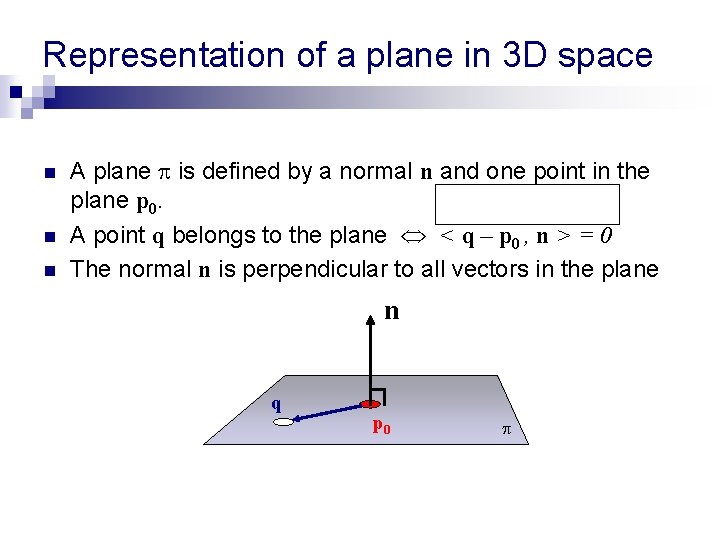
Representation of a plane in 3 D space n n n A plane is defined by a normal n and one point in the plane p 0. A point q belongs to the plane < q – p 0 , n > = 0 The normal n is perpendicular to all vectors in the plane n q p 0

Distance between point and plane n Project the point onto the plane in the direction of the normal: dist(q, ) = ||q’ – q|| q q’ n p 0

Distance between point and plane q q’ n p 0

Implicit representation of planes in 3 D Ax+By+Cz+D > 0 n n (x, y, z) are coordinates of a point on Ax+By+Cz+D = the 0 plane (A, B, C) are the coordinates of a normal vector to the plane Ax+By+Cz+D < 0

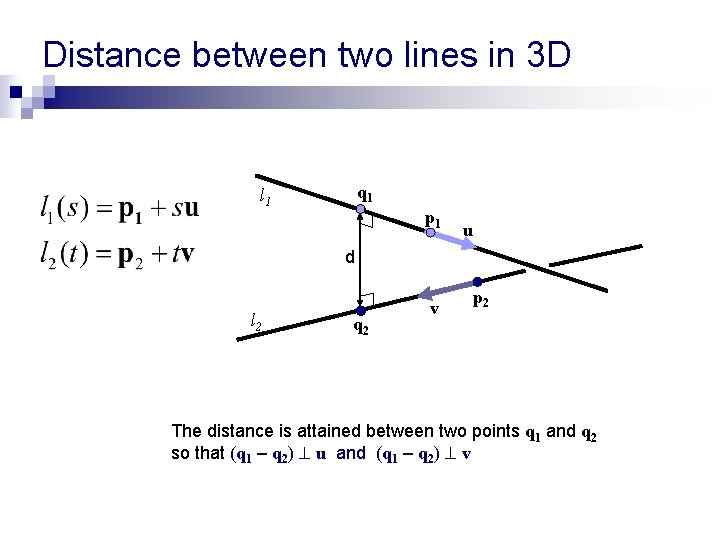
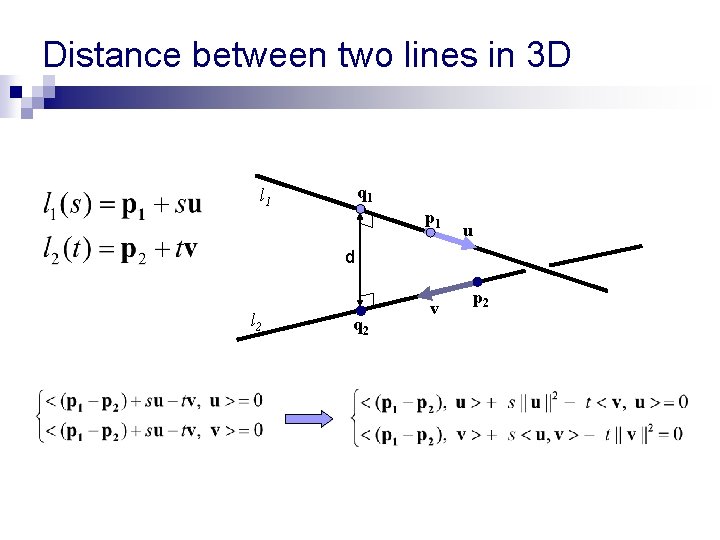
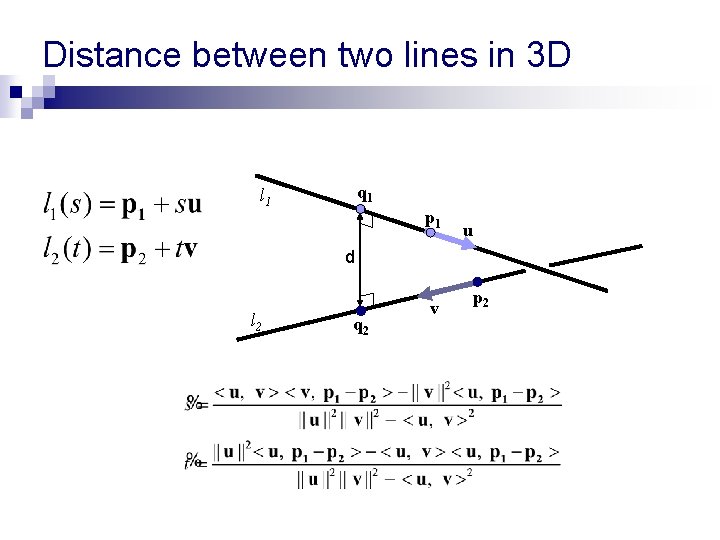
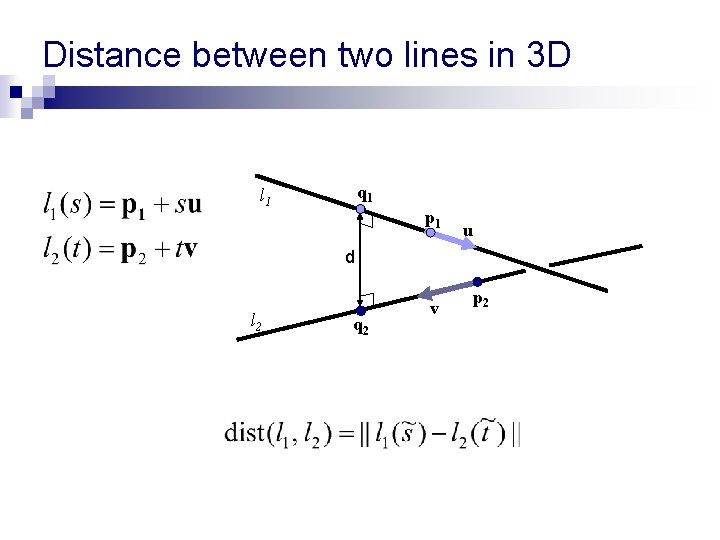
Distance between two lines in 3 D q 1 l 1 p 1 u d l 2 q 2 v p 2 The distance is attained between two points q 1 and q 2 so that (q 1 – q 2) u and (q 1 – q 2) v

Distance between two lines in 3 D q 1 l 1 p 1 u d l 2 q 2 v p 2

Distance between two lines in 3 D q 1 l 1 p 1 u d l 2 q 2 v p 2

Distance between two lines in 3 D q 1 l 1 p 1 u d l 2 q 2 v p 2

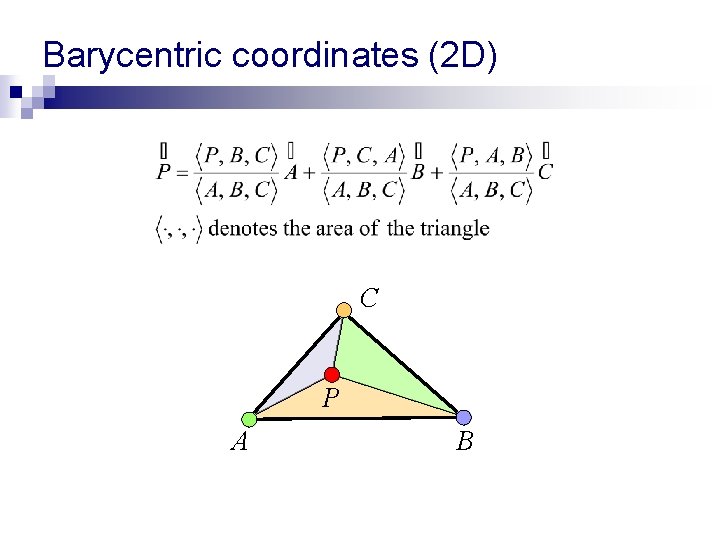
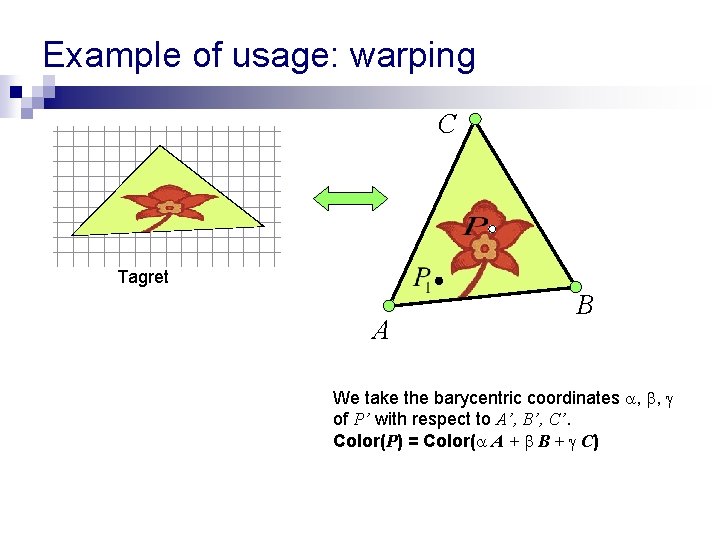
Barycentric coordinates (2 D) n n Define a point’s position relatively to some fixed points. P = A + B + C, where A, B, C are not on one line, and , , R. ( , , ) are called Barycentric coordinates of P with respect to A, B, C (unique!) If P is inside the triangle, then + + =1, , , > 0 C P A B

Barycentric coordinates (2 D) C P A B

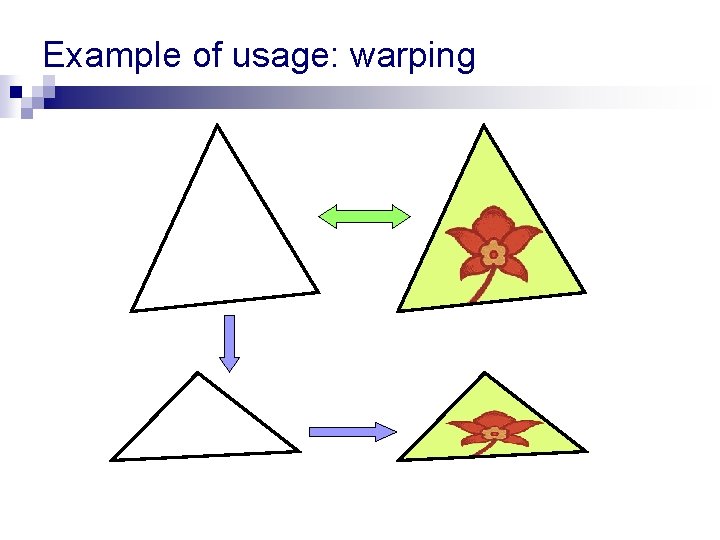
Example of usage: warping

Example of usage: warping C Tagret A B We take the barycentric coordinates , , of P’ with respect to A’, B’, C’. Color(P) = Color( A + B + C)

See you next time!