3 D Coordinates In the real world points





















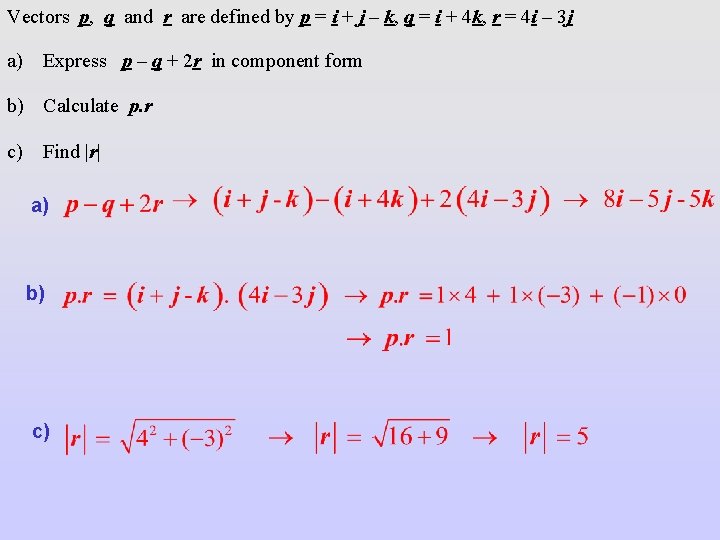










- Slides: 55

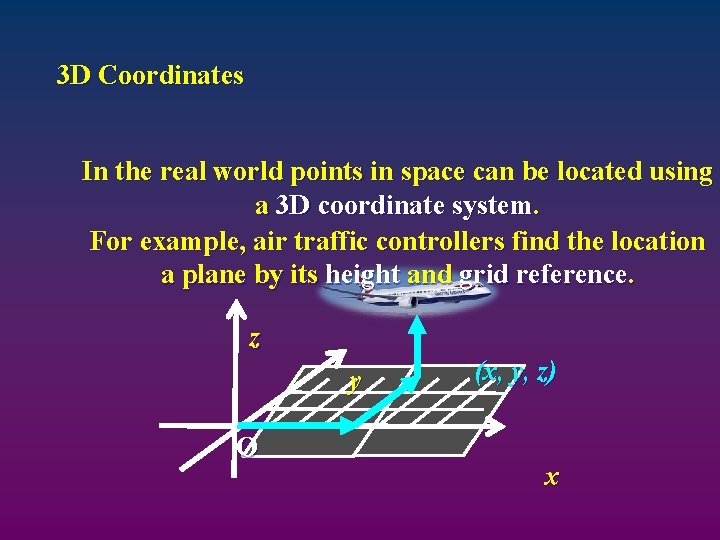
3 D Coordinates In the real world points in space can be located using a 3 D coordinate system. For example, air traffic controllers find the location a plane by its height and grid reference. z y O (x, y, z) x

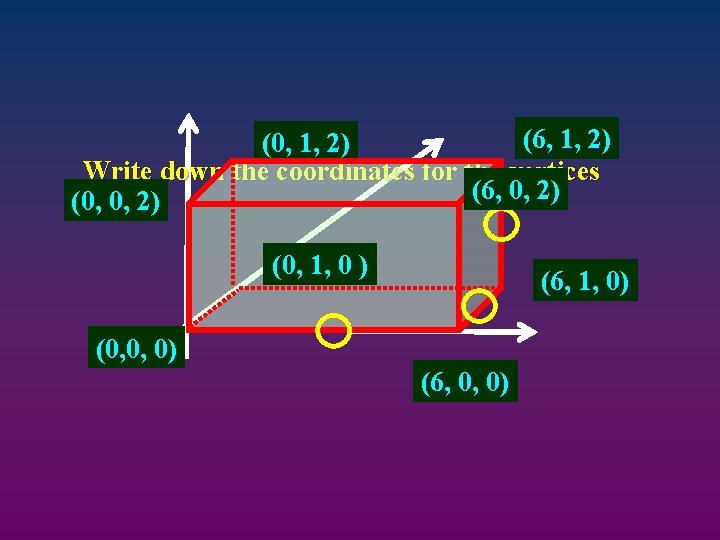
(6, 1, 2) (0, 1, 2) Write down the coordinates for the vertices (6, 0, 2) (0, 1, 0 ) (6, 1, 0) (0, 0, 0) (6, 0, 0)

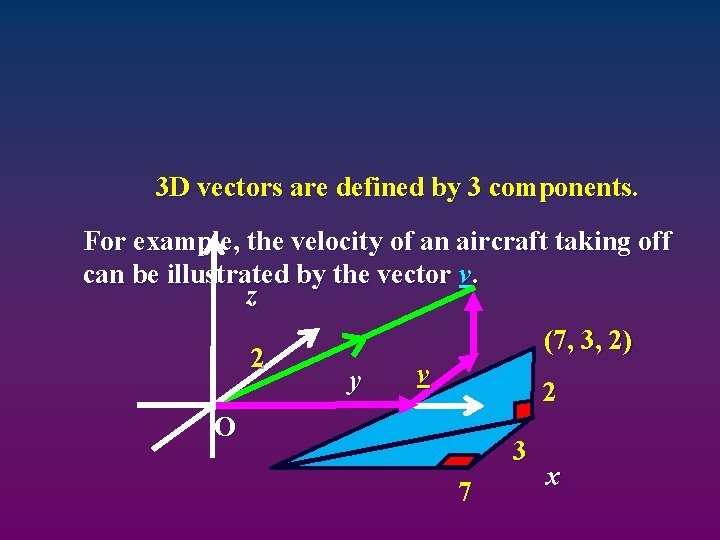
3 D vectors are defined by 3 components. For example, the velocity of an aircraft taking off can be illustrated by the vector v. z 2 (7, 3, 2) y v 2 O 3 7 x

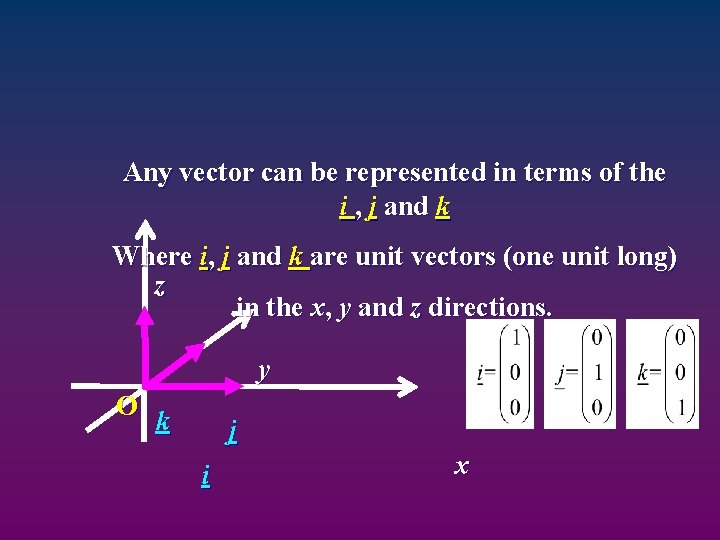
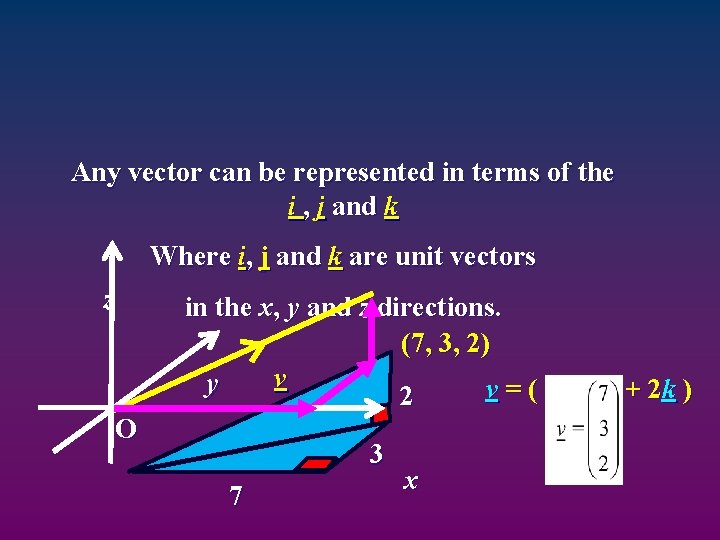
Any vector can be represented in terms of the i , j and k Where i, j and k are unit vectors (one unit long) z in the x, y and z directions. y O k j i x

Any vector can be represented in terms of the i , j and k Where i, j and k are unit vectors z in the x, y and z directions. (7, 3, 2) v y v = ( 7 i+ 3 j + 2 k ) 2 O 3 7 x

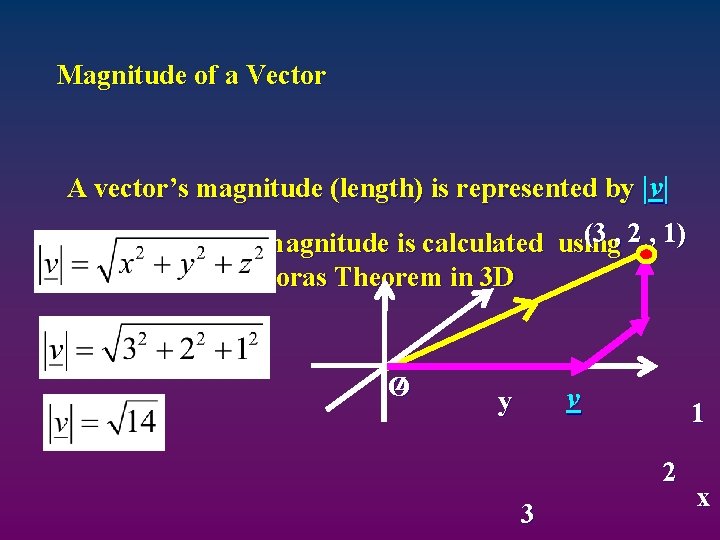
Magnitude of a Vector A vector’s magnitude (length) is represented by |v| (3 , 2 , 1) A 3 D vector’s magnitude is calculated using Pythagoras Theorem in 3 D z O v y 1 2 3 x

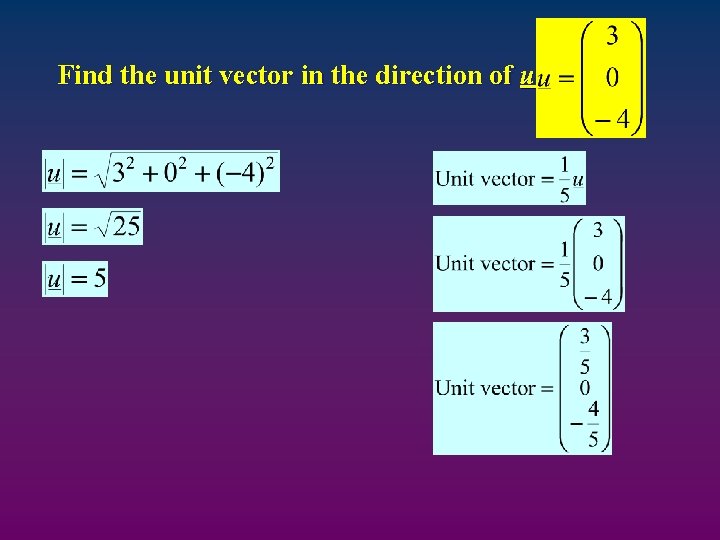
Find the unit vector in the direction of u

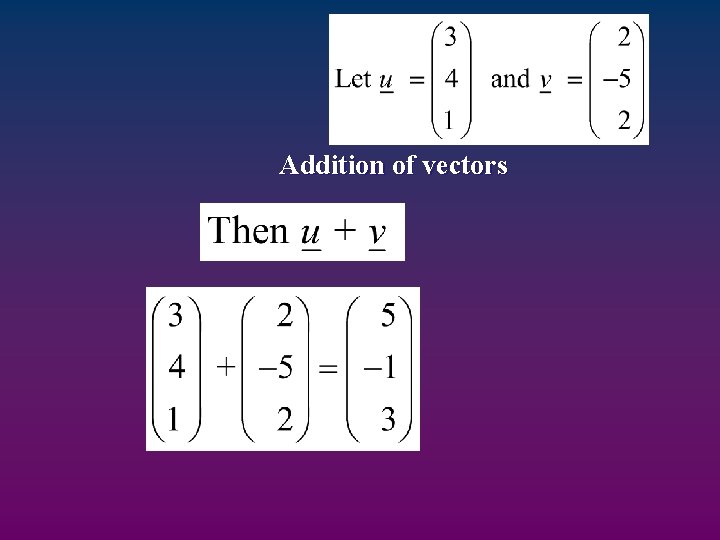
Addition of vectors

Addition of Vectors For vectors u and v

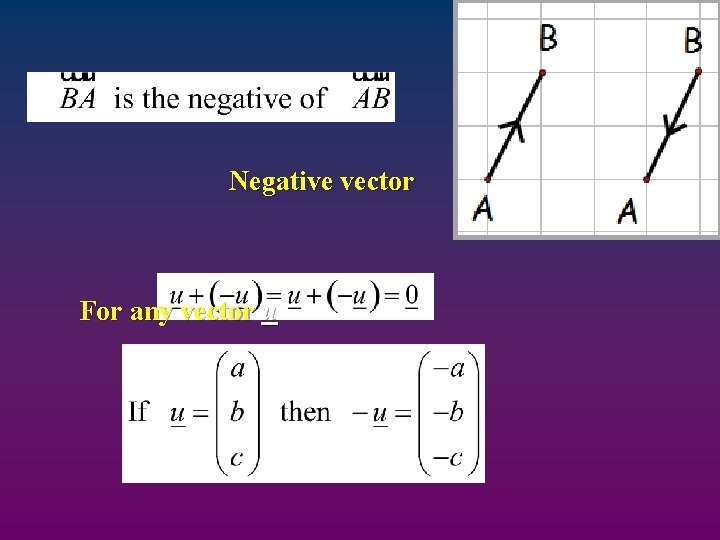
Negative vector For any vector u

Subtraction of vectors

Subtraction of Vectors For vectors u and v

Multiplication by a scalar ( a number) Hence if u = kv then u is parallel to v Conversely if u is parallel to v then u = kv

Combining. Vectors

Show that the two vectors are parallel. If z = kw then z is parallel to w

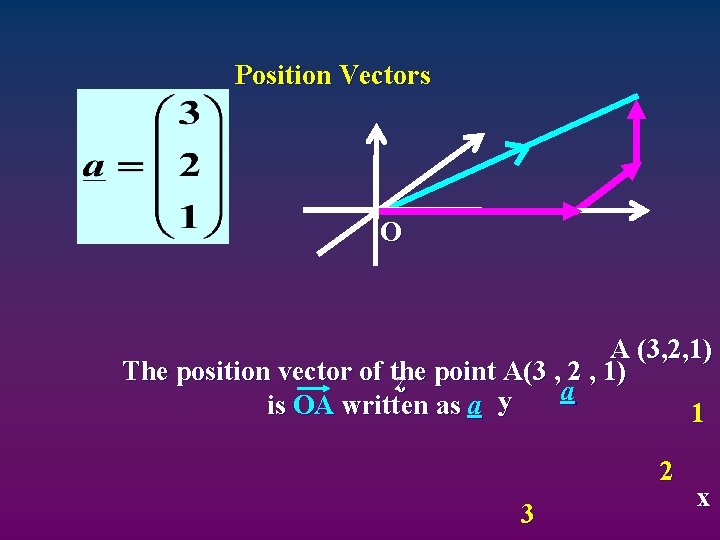
Position Vectors O A (3, 2, 1) The position vector of the z point A(3 , a 2 , 1) is OA written as a y 1 2 3 x

Position If R is ( Vectors 2 , -5 , 1) and S is (4 , 1 , -3) 4 2 2 Then RS is s – r = 1 – -5 = 6 -3 1 -4

Position as a. Sjourney If R is ( Vectors 2 , -5 , 1) and is (4 , 1 , -3) x component of RS is 2 to 4 = 2 y component of RS is -5 to 1 = 6 z component of RS is 1 to -3 = -4 2 RS = 6 -4

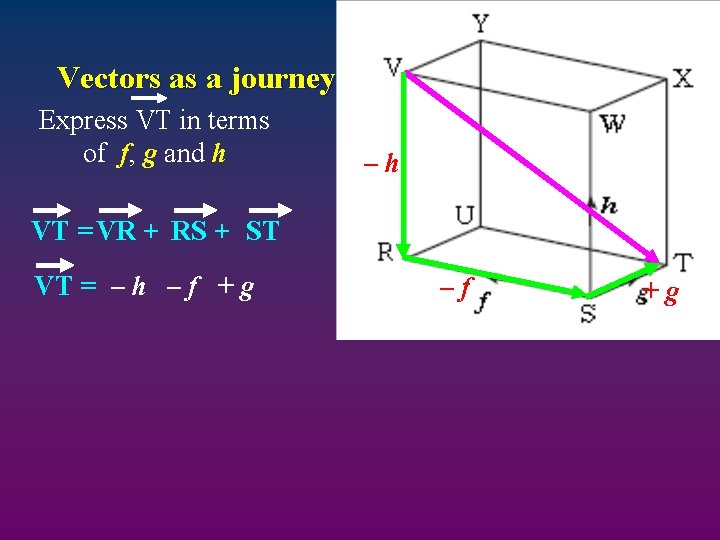
Vectors as a journey Express VT in terms of f, g and h –h VT = VR + RS + ST VT = – h – f + g –f +g

A is (0 , -3 , 5), B is (7 , -6 , 9) and C is (21 , -12 , 17). Show Collinear Points that A , B and C are collinear stating the ratio AB: BC. BC = 2 AB AB and BC are parallel (multiples of each other) through the common point B, and so must be collinear A 1 B 2 AB : BC = 1 : 2 C

Given that the points S(– 4, 5, 1), T(– 16, – 4, 16) and U( Collinear Points – 24, – 10, 26) are collinear, calculate the ratio in which T divides SU. S 3 T 2 ST : TU = 3 : 2 U

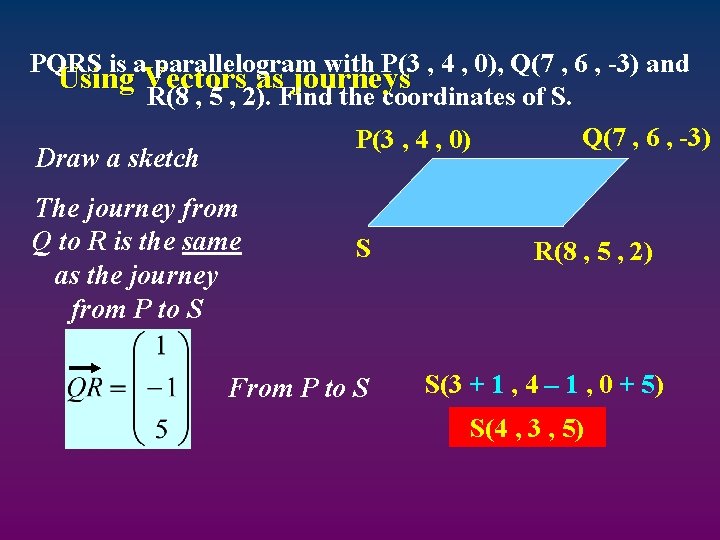
PQRS is a parallelogram with P(3 , 4 , 0), Q(7 , 6 , -3) and Using Vectors as journeys R(8 , 5 , 2). Find the coordinates of S. P(3 , 4 , 0) Draw a sketch The journey from Q to R is the same as the journey from P to S S From P to S Q(7 , 6 , -3) R(8 , 5 , 2) S(3 + 1 , 4 – 1 , 0 + 5) S(4 , 3 , 5)

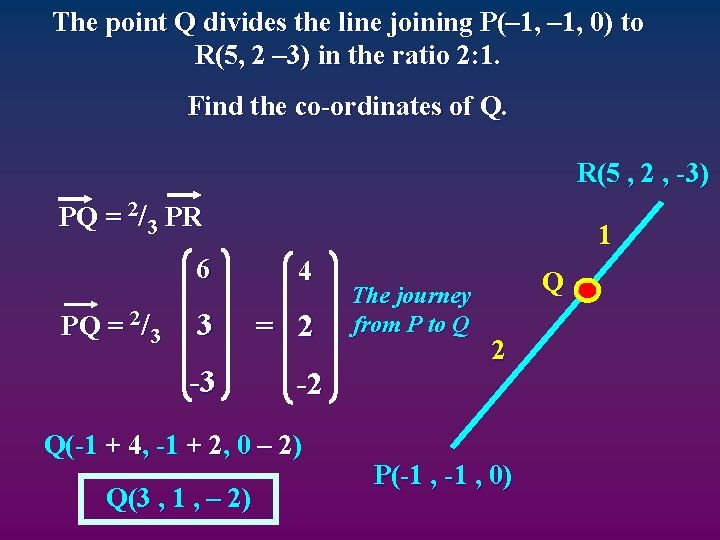
The point Q divides the line joining P(– 1, 0) to R(5, 2 – 3) in the ratio 2: 1. Find the co-ordinates of Q. R(5 , 2 , -3) PQ = 2/3 PR PQ = 2/3 1 6 4 3 = 2 -3 -2 Q(-1 + 4, -1 + 2, 0 – 2) Q(3 , 1 , – 2) The journey from P to Q Q 2 P(-1 , 0)

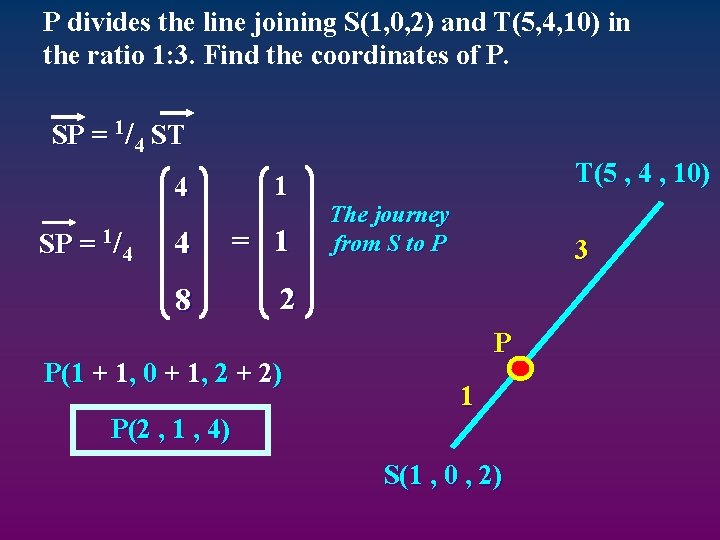
P divides the line joining S(1, 0, 2) and T(5, 4, 10) in the ratio 1: 3. Find the coordinates of P. SP = 1/4 ST SP = 1/4 4 1 4 = 1 8 2 P(1 + 1, 0 + 1, 2 + 2) P(2 , 1 , 4) T(5 , 4 , 10) The journey from S to P 3 P 1 S(1 , 0 , 2)

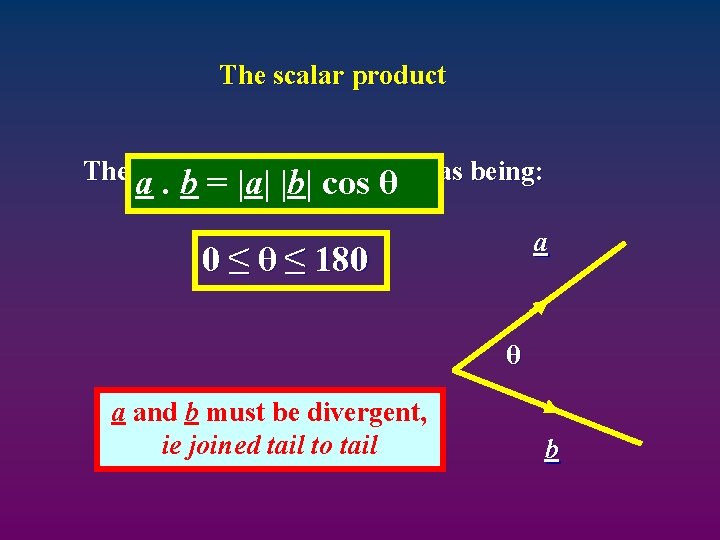
The scalar product The a scalar defined. b =product |a| |b| iscos θ as being: a 0 ≤ θ ≤ 180 θ a and b must be divergent, ie joined tail to tail b

The Scalar Product o a. b = |a| |b| cos θ a. b = 4 × 5 cos 45 Find the scalar product for a and b when o a (a). b =θ 20 × o 1/√ 2(b) ×θ √ 2 |a|= 4 , |b|= 5 when = 45 = /90 √ 2 a. b = 10√ 2 a. b = |a| |b| cos θ a. b = 4 × 5 cos 90 o a. b = 20 × 0 a. b=0 When θ = 90 o

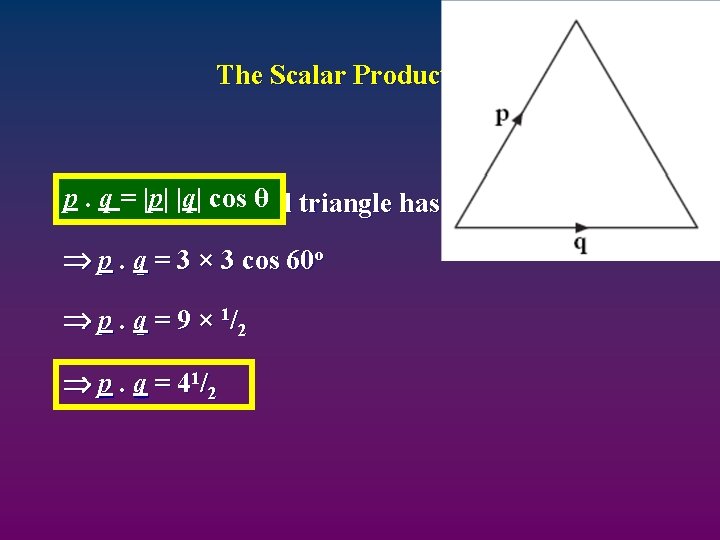
The Scalar Product p. q. This = |p|equilateral |q| cos θ triangle has sides of 3 units. p. q = 3 × 3 cos 60 o p. q = 9 × 1/ 2 p. q = 41/2

The Scalar Product r r p. (q + r)= p. q + p. r 60 o This equilateral triangle has sides of 3 units. p. (q + r) p. q = 3 × 3 cos 60 o p and r are not p. q=3× 3×½ divergent so move r p. q = 41/2 p. r = 3 × 3 cos 60 o p. r=9 ½ p. (q + r) = p. q + p. r = 9 p. r = 4½

If a and b are perpendicular then a. b=0

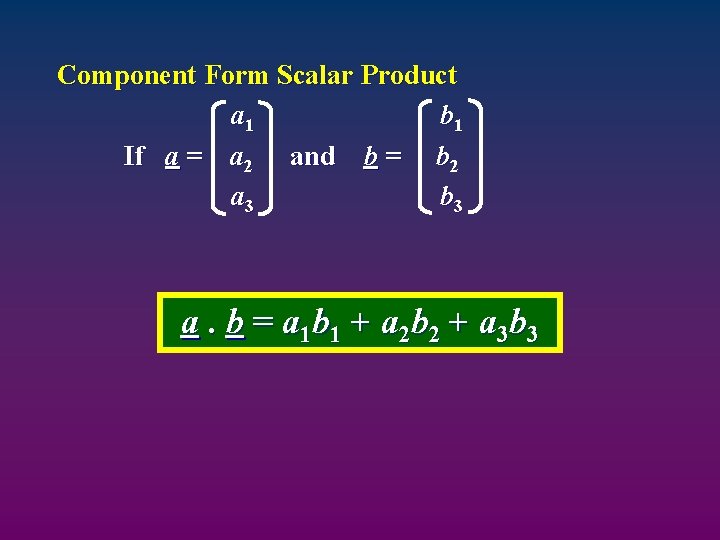
Component Form Scalar Product a 1 b 1 If a = a 2 and b = b 2 a 3 b 3 a. b = a 1 b 1 + a 2 b 2 + a 3 b 3

Angle between Vectors To find the angle between two vectors we simply use. b = a 1 b 1 rearranged + a 2 b 2 + a 3 b 3 a. b = the |a| |b| cos θproduct aformulae scalar cos θ = a. b |a| |b| cos θ = a 1 b 1 + a 2 b 2 + a 3 b 3 |a| |b|

p = 3 i + 2 j + 5 k and q = 4 i + j + 3 k 3 |p| = √(32 + 22 + 52) 4 |q| = √(42 + 12 + 32) p= 2 q= 1 |q| = √ 26 |p| =the √ 38 angle between the 5 Find 3 two vectors below. a. b = a 1 b 1 + a 2 b 2 + a 3 b 3 = 3× 4 + 2× 1 + 5× 3 = 29 a 1 b 1 + a 2 b 2 + a 3 b 3 cos θ = = |a| |b| 29 = 0∙ 923 √ 38 × √ 26 θ = cos-1 0∙ 923 = 22∙ 7 o

a Perpendicular. b = | a | | b | cos Ɵ Vectors If a and b are perpendicular then a. b = 0 cos 90 o = 0 If a and b are perpendicular then + a 2 b 2 + a 3 b 3 = 0 a 1 b 1

If a and b are perpendicular then a. b = 0 if a = 3 2 -1 a. b = a 1 b 1 + a 2 b 2 + a 3 b 3 and b = 1 2 7 a. b = 3× 1 + 2× 2 + (-1)× 7 a. b=3+4 – 7 a. b=0 a and b are perpendicular

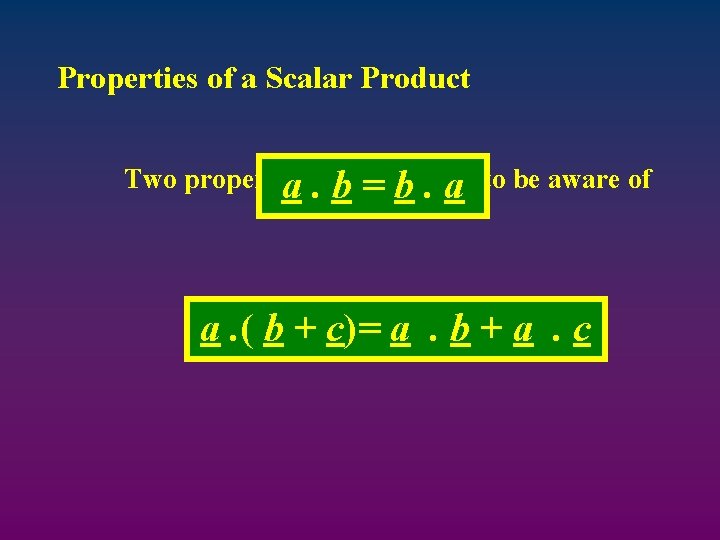
Properties of a Scalar Product Two properties a. that b =youb need. a to be aware of a. ( b + c)= a. b + a. c

If | p | = 5 and | q | = 4, find p. (p + q) p 60 o p. (p + q) = p. p + p. q q = | p | × | p |cos 0 o + | p | × | q |cos 60 o =5× 5× 1+5× 4×½ = 25 + 10 = 35

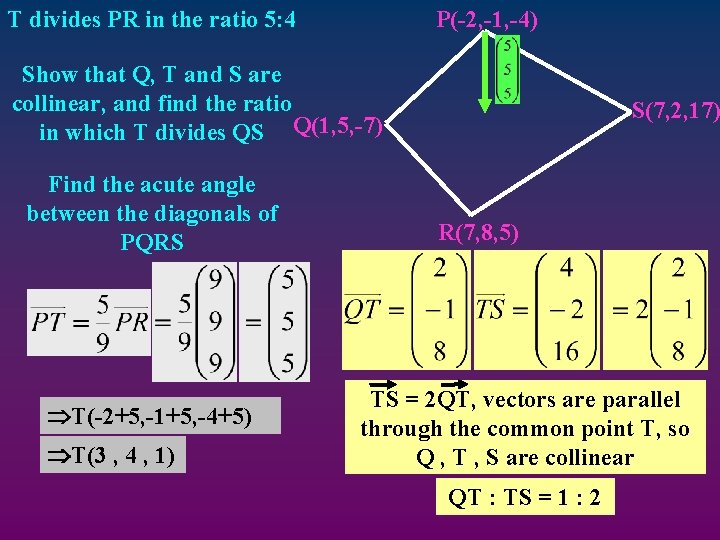
T divides PR in the ratio 5: 4 P(-2, -1, -4) Show that Q, T and S are collinear, and find the ratio in which T divides QS Q(1, 5, -7) Find the acute angle between the diagonals of PQRS T(-2+5, -1+5, -4+5) T(3 , 4 , 1) S(7, 2, 17) R(7, 8, 5) TS = 2 QT, vectors are parallel through the common point T, so Q , T , S are collinear QT : TS = 1 : 2

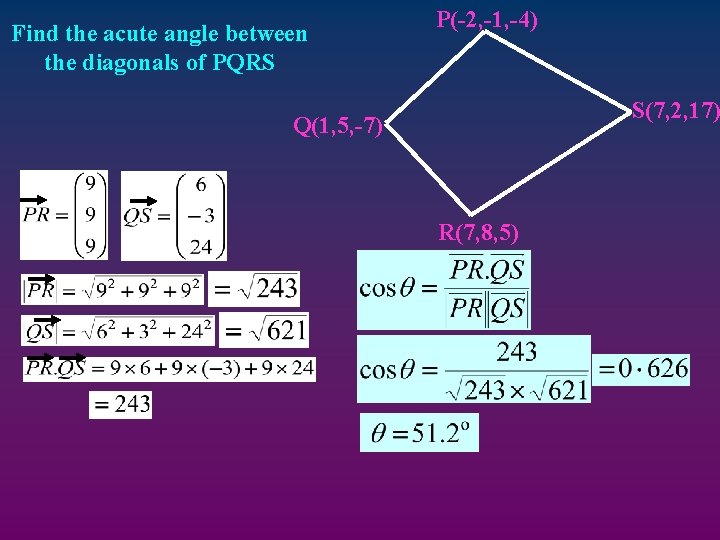
Find the acute angle between the diagonals of PQRS P(-2, -1, -4) S(7, 2, 17) Q(1, 5, -7) R(7, 8, 5)

Vectors u and v are defined by u = 3 i + 2 j and v = 2 i – 3 j + 4 k Determine whether or not u and v are perpendicular. 3 u. v = 2. 0 2 -3 4 u. v = 3× 2 + 2×(-3) + 0× 4 u. v=6– 6 +0 u. v=0 Hence vectors are perpendicular

For what value of t are the vectors u and v perpendicular ? u. v = 0 if vectors perpendicular t u. v = -2 3 . 2 10 t u. v = t × 2 + (-2)× 10 + 3×t u. v = 5 t – 20 u. v = 0 5 t – 20 = 0 t=4

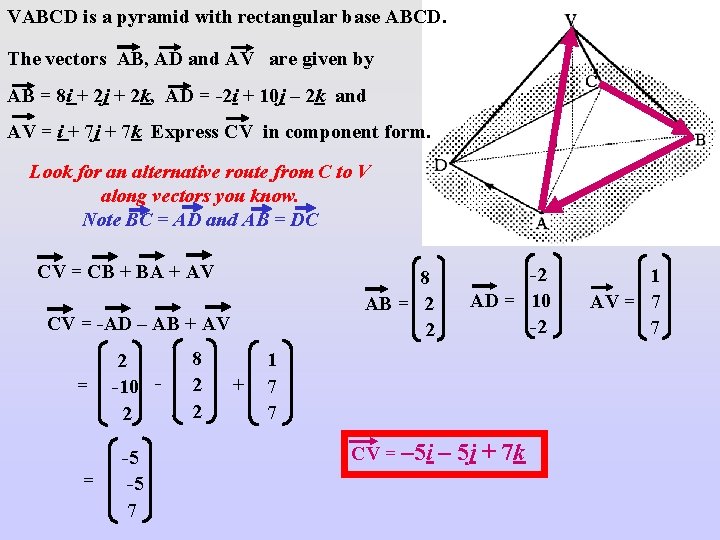
VABCD is a pyramid with rectangular base ABCD. The vectors AB, AD and AV are given by AB = 8 i + 2 j + 2 k, AD = -2 i + 10 j – 2 k and AV = i + 7 j + 7 k Express CV in component form. Look for an alternative route from C to V along vectors you know. Note BC = AD and AB = DC CV = CB + BA + AV 8 AB = 2 2 CV = -AD – AB + AV = = 2 -10 2 -5 -5 7 8 2 2 + -2 AD = 10 -2 1 7 7 CV = – 5 i – 5 j + 7 k 1 AV = 7 7

The diagram shows two vectors a and b, with | a | = 3 and | b | = 2 2. These vectors are inclined at an angle of 45° to each other. a) Evaluate i) a. a ii) b. b iii) a. b b) Another vector p is defined by p = 2 a + 3 b Evaluate p. p and hence write down | p |. i) iii) b) p 2
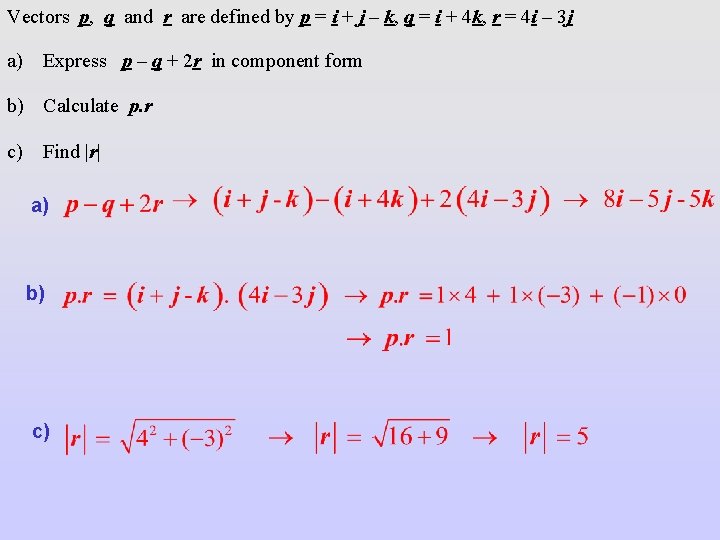
Vectors p, q and r are defined by p = i + j – k, q = i + 4 k, r = 4 i – 3 j a) Express p – q + 2 r in component form b) Calculate p. r c) Find |r| a) b) c)

The diagram shows a point P with co-ordinates (4, 2, 6) and two points S and T which lie on the x-axis. If P is 7 units from S and 7 units from T, find the co-ordinates of S and T. hence there are 2 points on the x axis that are 7 units from Pi. e. and S and T

The position vectors of the points P and Q are p = –i + 3 j + 4 k and q = 7 i – j + 5 k respectively. a) Express PQ in component form. b) Find the length of PQ.

P PQR is an equilateral triangle of side 2 units. a 60° b Evaluate a. (b + c) and hence identify two vectors which are perpendicular. Q 60° 120 o 60° c NB for a. c vectors must diverge ( so angle is 120° ) Hence so, a is perpendicular to b+c R

Calculate the length of the vector 2 i – 3 j + 3 k Length

Find the value of k for which the vectors perpendicular Put Scalar product = 0 and are

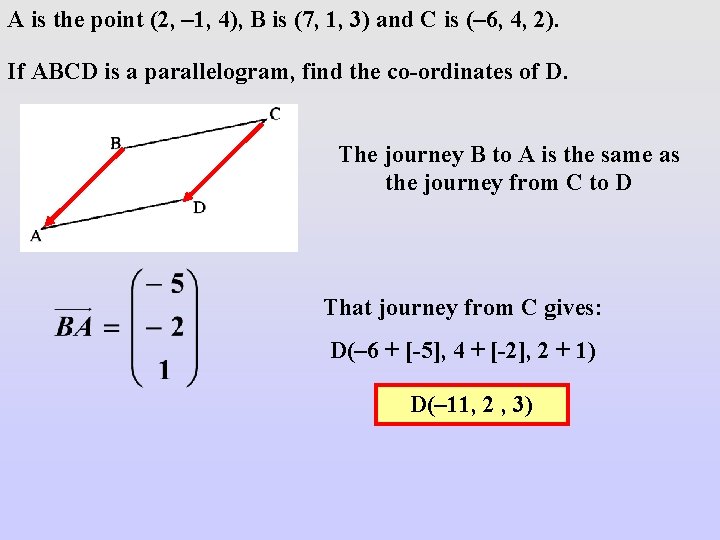
A is the point (2, – 1, 4), B is (7, 1, 3) and C is (– 6, 4, 2). If ABCD is a parallelogram, find the co-ordinates of D. The journey B to A is the same as the journey from C to D That journey from C gives: D(– 6 + [-5], 4 + [-2], 2 + 1) D(– 11, 2 , 3)

The vectors a, b and c are defined as follows: a = 2 i – k, b = i + 2 j + k, a) Evaluate a. b + a. c c = –j + k b) From your answer to (a), make a deduction about the vector b + c a) b) b + c is perpendicular to a

In the square based pyramid, all the eight edges are of length 3 units. Evaluate p. (q + r) Triangular faces are all equilateral

A and B are the points (-1, -3, 2) and (2, -1, 1) respectively. (-1, -3, 2) B and C are the points of trisection of AD. That is, AB = BC = CD. Find the coordinates of D D is (-1 + 9, -3 + 6, 2 – 3) D is (8, 3, – 1) (2, -1, 1)

The point Q divides the line joining P(– 1, 0) to R(5, 2 – 3) in the ratio 2: 1. R 1 Q Find the co-ordinates of Q. 2 (5, 2, -3) P (-1, 0) Q is (-1 + 4, -1 + 2, 0 – 2) Q is (3, 1, – 2)

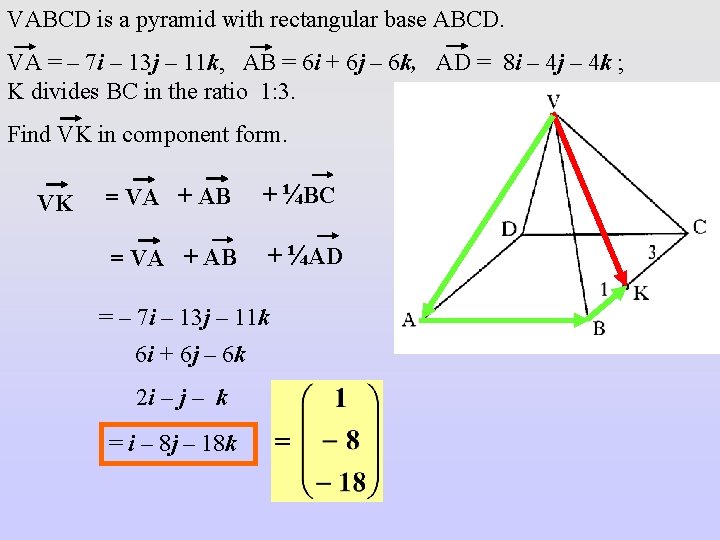
VABCD is a pyramid with rectangular base ABCD. VA = – 7 i – 13 j – 11 k, AB = 6 i + 6 j – 6 k, AD = 8 i – 4 j – 4 k ; K divides BC in the ratio 1: 3. Find VK in component form. VK = VA + AB + ¼BC = VA + AB + ¼AD = – 7 i – 13 j – 11 k 6 i + 6 j – 6 k 2 i – j – k = i – 8 j – 18 k

A is the point (2, – 5, 6), B is (6, – 3, 4) and C is (12, 0, 1). Show that A, B and C are collinear and determine the ratio in which B divides AC AB and BC are scalar multiples, so are parallel. B is common. A, B, C are collinear A 2 B 3 C B divides AB in ratio 2 : 3