3 D Computer Vision 3 D Vision and




































- Slides: 58

3 D Computer Vision 3 D Vision and Video Computing CSc I 6716 Fall 2005 Topic 4 of Part II Stereo Vision Zhigang Zhu, City College of New York zhu@cs. ccny. cuny. edu

3 D Computer Vision and Video Computing n Problem l n Infer 3 D structure of a scene from two or more images taken from different viewpoints Two primary Sub-problems l Correspondence problem (stereo match) -> disparity map n n l Similarity instead of identity Occlusion problem: some parts of the scene are visible only in one eye Reconstruction problem -> 3 D n n n Stereo Vision What we need to know about the cameras’ parameters Often a stereo calibration problem Lectures on Stereo Vision l l l Stereo Geometry – Epipolar Geometry (*) Correspondence Problem (*) – Two classes of approaches 3 D Reconstruction Problems – Three approaches

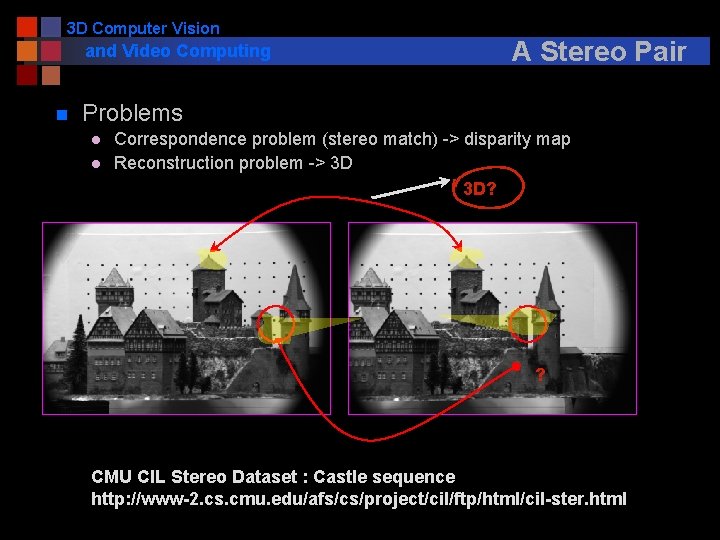
3 D Computer Vision and Video Computing n A Stereo Pair Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D 3 D? ? CMU CIL Stereo Dataset : Castle sequence http: //www-2. cs. cmu. edu/afs/cs/project/cil/ftp/html/cil-ster. html

3 D Computer Vision and Video Computing n More Images… Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D

3 D Computer Vision and Video Computing n More Images… Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D

3 D Computer Vision and Video Computing n More Images… Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D

3 D Computer Vision and Video Computing n More Images… Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D

3 D Computer Vision and Video Computing n More Images… Problems l l Correspondence problem (stereo match) -> disparity map Reconstruction problem -> 3 D

3 D Computer Vision and Video Computing n A Simple Stereo Vision System l l l n Disparity Equation Depth Resolution Fixated Stereo System n Zero-disparity Horopter Epipolar Geometry l Epipolar lines – Where to search correspondences n Epipolar Plane, Epipolar Lines and Epipoles n l n Part I. Stereo Geometry http: //www. ai. sri. com/~luong/research/Meta 3 DViewer/Epipolar. Geo. html Essential Matrix and Fundamental Matrix n Computing E & F by the Eight-Point Algorithm n Computing the Epipoles Stereo Rectification

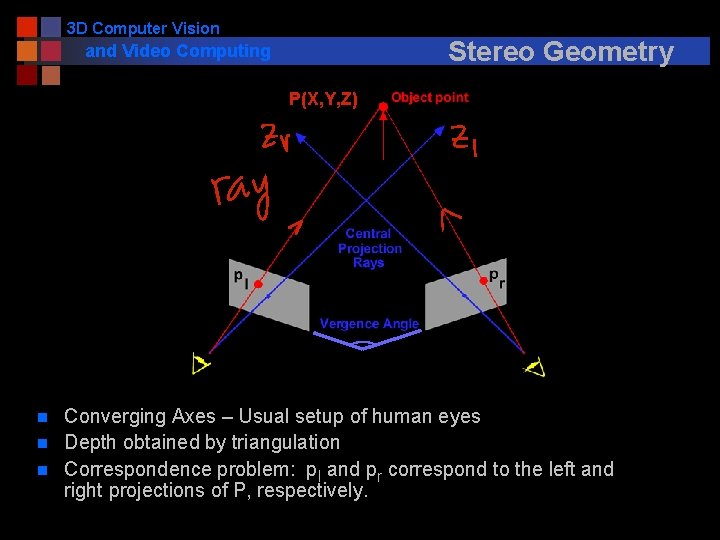
3 D Computer Vision Stereo Geometry and Video Computing P(X, Y, Z) n n n Converging Axes – Usual setup of human eyes Depth obtained by triangulation Correspondence problem: pl and pr correspond to the left and right projections of P, respectively.

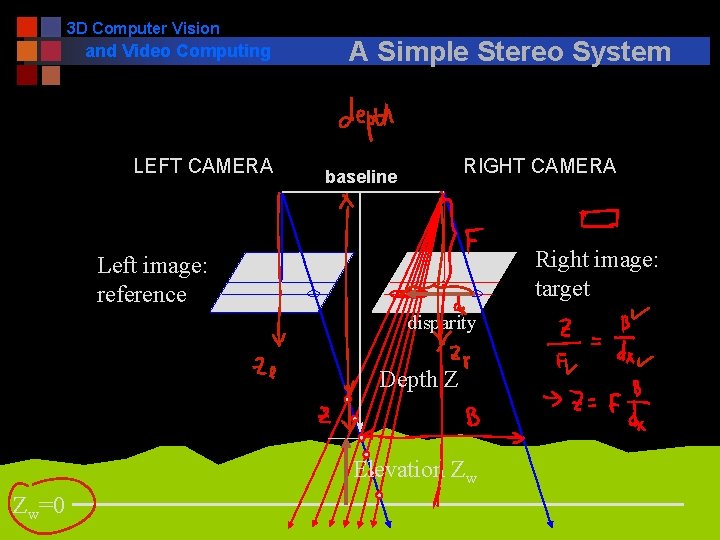
3 D Computer Vision and Video Computing LEFT CAMERA A Simple Stereo System RIGHT CAMERA baseline Right image: target Left image: reference disparity Depth Z Elevation Zw Zw=0

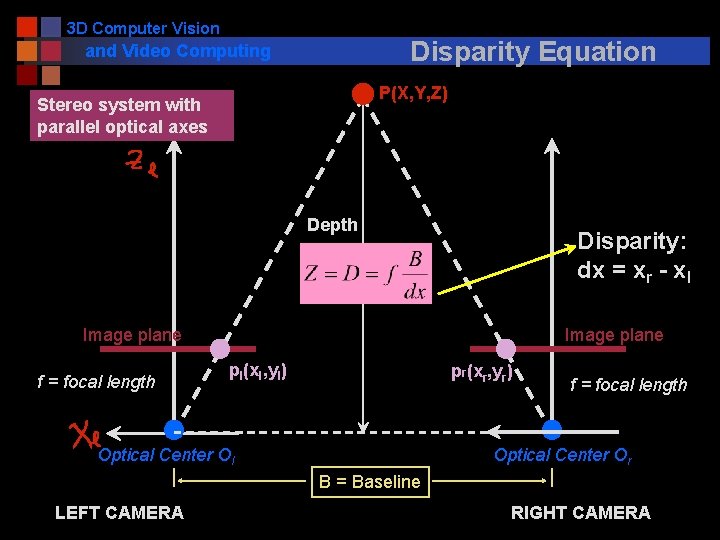
3 D Computer Vision Disparity Equation and Video Computing P(X, Y, Z) Stereo system with parallel optical axes Depth Disparity: dx = xr - xl Image plane f = focal length Image plane pl(xl, yl) pr(xr, yr) Optical Center Ol f = focal length Optical Center Or B = Baseline LEFT CAMERA RIGHT CAMERA

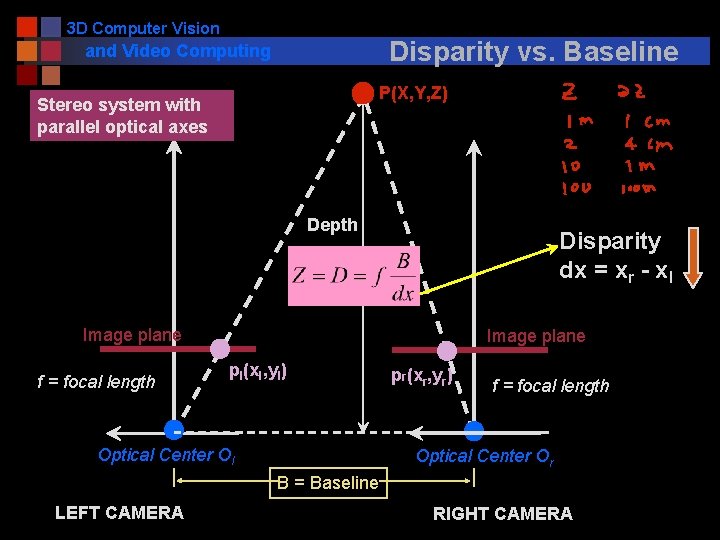
3 D Computer Vision Disparity vs. Baseline and Video Computing P(X, Y, Z) Stereo system with parallel optical axes Depth Disparity dx = xr - xl Image plane f = focal length Image plane pl(xl, yl) Optical Center Ol pr(xr, yr) f = focal length Optical Center Or B = Baseline LEFT CAMERA RIGHT CAMERA

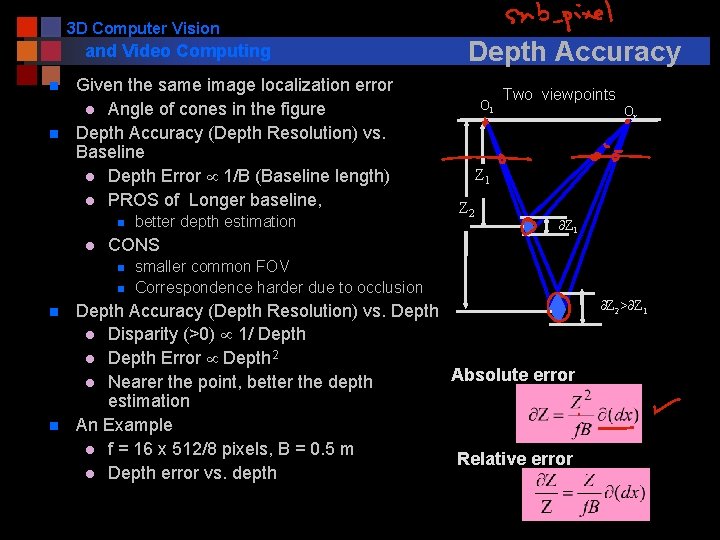
3 D Computer Vision and Video Computing n n Given the same image localization error l Angle of cones in the figure Depth Accuracy (Depth Resolution) vs. Baseline l Depth Error 1/B (Baseline length) l PROS of Longer baseline, n l CONS n n better depth estimation Depth Accuracy Ol Two viewpoints Or Z 1 Z 2 Z 1 smaller common FOV Correspondence harder due to occlusion Depth Accuracy (Depth Resolution) vs. Depth l Disparity (>0) 1/ Depth l Depth Error Depth 2 Absolute error l Nearer the point, better the depth estimation An Example l f = 16 x 512/8 pixels, B = 0. 5 m Relative error l Depth error vs. depth Z 2> Z 1

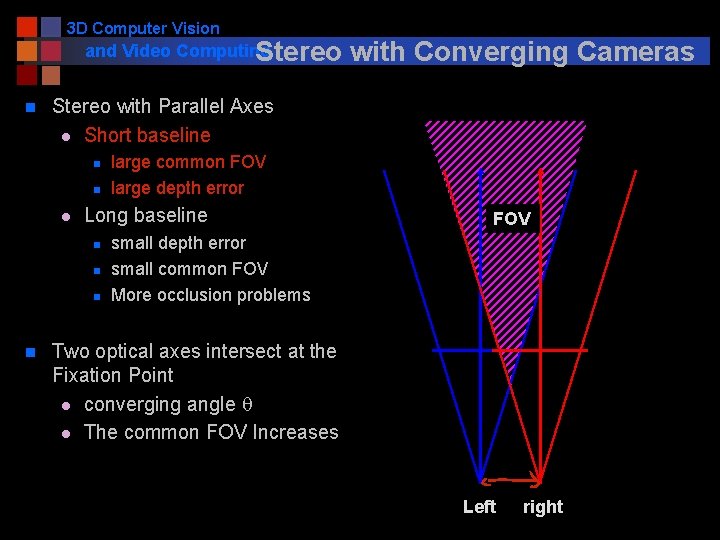
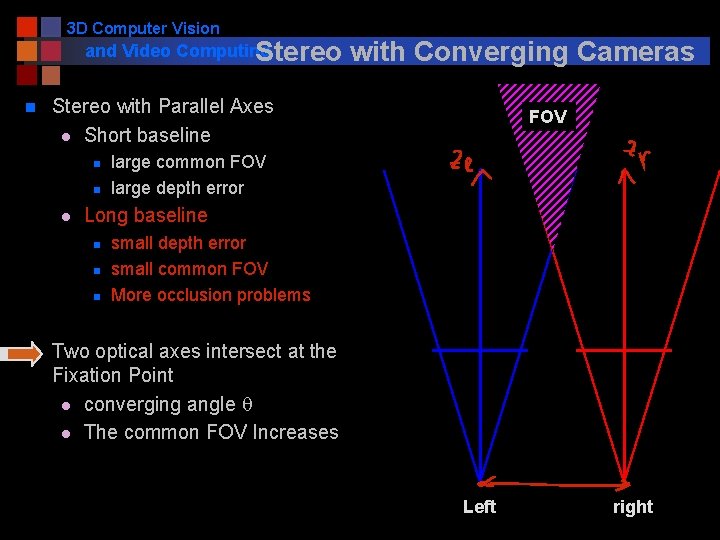
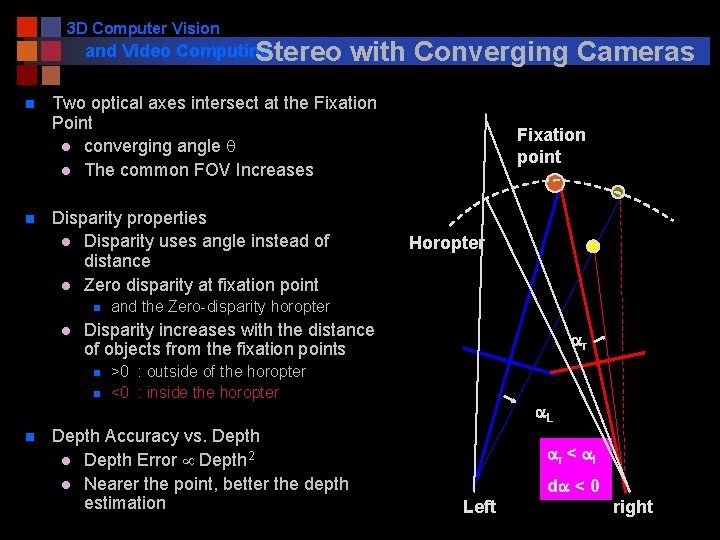
3 D Computer Vision and Video Computing Stereo n Stereo with Parallel Axes l Short baseline n n l large common FOV large depth error Long baseline n n with Converging Cameras FOV small depth error small common FOV More occlusion problems Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Left right

3 D Computer Vision and Video Computing Stereo n Stereo with Parallel Axes l Short baseline n n l FOV large common FOV large depth error Long baseline n n with Converging Cameras small depth error small common FOV More occlusion problems Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Left right

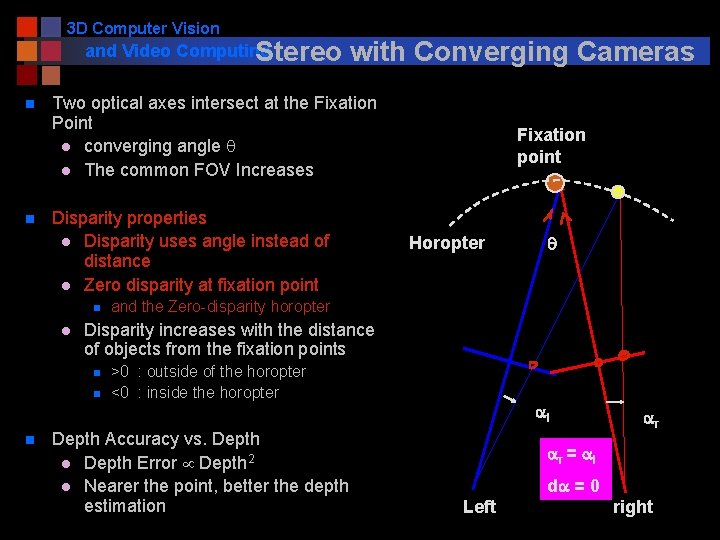
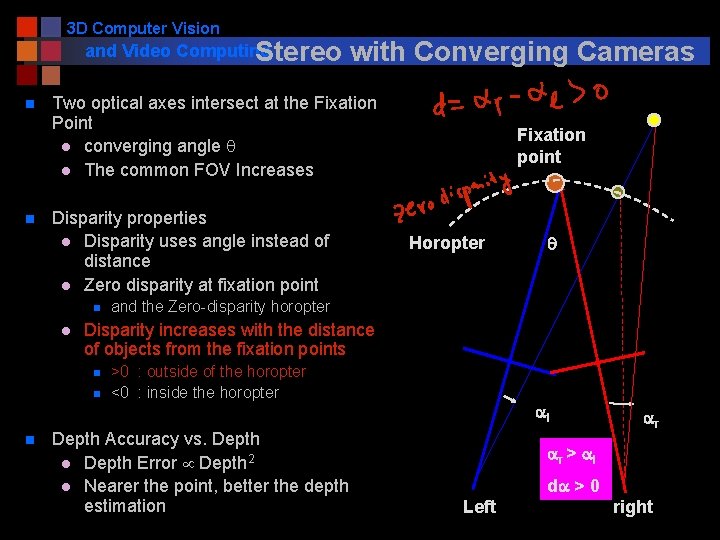
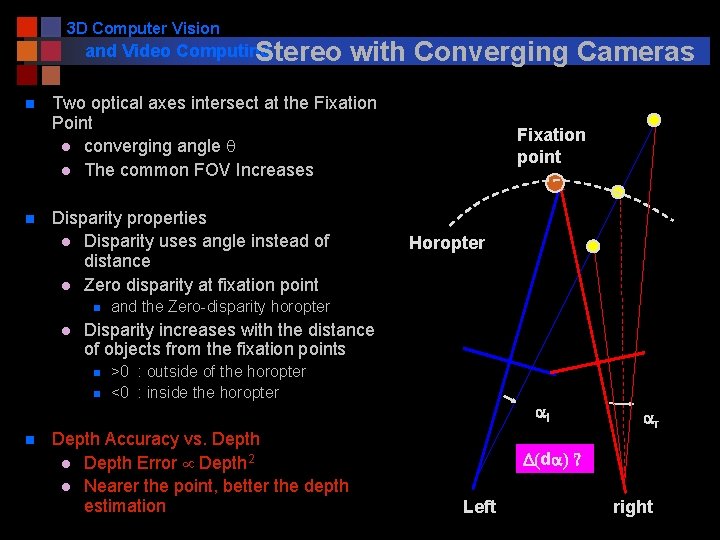
3 D Computer Vision and Video Computing Stereo n n Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Fixation point FOV Disparity properties l Disparity uses angle instead of distance l Zero disparity at fixation point n l q and the Zero-disparity horopter Disparity increases with the distance of objects from the fixation points n n n with Converging Cameras >0 : outside of the horopter <0 : inside the horopter Depth Accuracy vs. Depth l Depth Error Depth 2 l Nearer the point, better the depth estimation Left right

3 D Computer Vision and Video Computing Stereo n n Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Disparity properties l Disparity uses angle instead of distance l Zero disparity at fixation point n l Fixation point Horopter q and the Zero-disparity horopter Disparity increases with the distance of objects from the fixation points n n n with Converging Cameras >0 : outside of the horopter <0 : inside the horopter Depth Accuracy vs. Depth l Depth Error Depth 2 l Nearer the point, better the depth estimation al ar ar = al da = 0 Left right

3 D Computer Vision and Video Computing Stereo n n Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Disparity properties l Disparity uses angle instead of distance l Zero disparity at fixation point n l Fixation point Horopter q and the Zero-disparity horopter Disparity increases with the distance of objects from the fixation points n n n with Converging Cameras >0 : outside of the horopter <0 : inside the horopter Depth Accuracy vs. Depth l Depth Error Depth 2 l Nearer the point, better the depth estimation al ar ar > al da > 0 Left right

3 D Computer Vision and Video Computing Stereo n n Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Disparity properties l Disparity uses angle instead of distance l Zero disparity at fixation point n l Fixation point Horopter and the Zero-disparity horopter Disparity increases with the distance of objects from the fixation points n n n with Converging Cameras ar >0 : outside of the horopter <0 : inside the horopter Depth Accuracy vs. Depth l Depth Error Depth 2 l Nearer the point, better the depth estimation a. L ar < al da < 0 Left right

3 D Computer Vision and Video Computing Stereo n n Two optical axes intersect at the Fixation Point l converging angle q l The common FOV Increases Disparity properties l Disparity uses angle instead of distance l Zero disparity at fixation point n l Fixation point Horopter and the Zero-disparity horopter Disparity increases with the distance of objects from the fixation points n n n with Converging Cameras >0 : outside of the horopter <0 : inside the horopter Depth Accuracy vs. Depth l Depth Error Depth 2 l Nearer the point, better the depth estimation al ar D(da) ? Left right

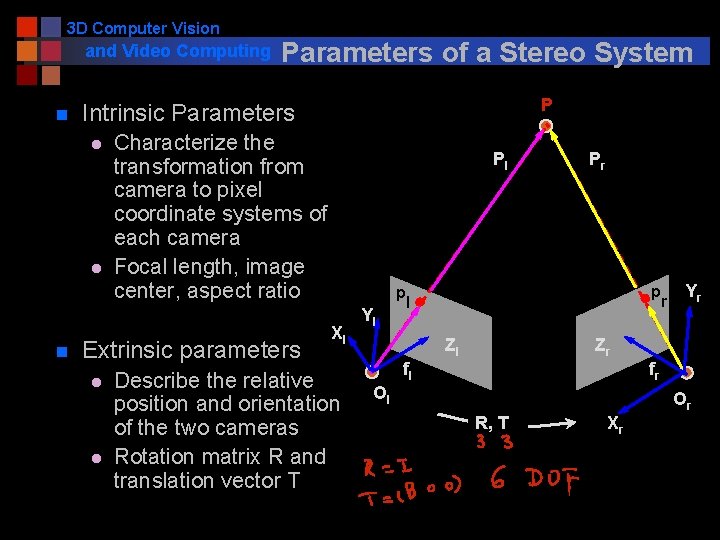
3 D Computer Vision and Video Computing n P Intrinsic Parameters l l n Parameters of a Stereo System Characterize the transformation from camera to pixel coordinate systems of each camera Focal length, image center, aspect ratio Extrinsic parameters l l Pl p Xl Describe the relative position and orientation of the two cameras Rotation matrix R and translation vector T Yl Pr p l Zl r Yr Zr fl fr Ol Or R, T Xr

3 D Computer Vision Epipolar Geometry and Video Computing n P Notations l Pl =(Xl, Yl, Zl), Pr =(Xr, Yr, Zr) n l Pl Vectors of the same 3 -D point P, in the left and right camera coordinate systems respectively Extrinsic Parameters n n Translation Vector T = (Or-Ol) Rotation Matrix R p Yl Xl l Pr pl =(xl, yl, zl), pr =(xr, yr, zr) n n Projections of P on the left and right image plane respectively For all image points, we have zl=fl, zr=fr Ol p l fl Zl Zr R, T Xr r Yr fr Or

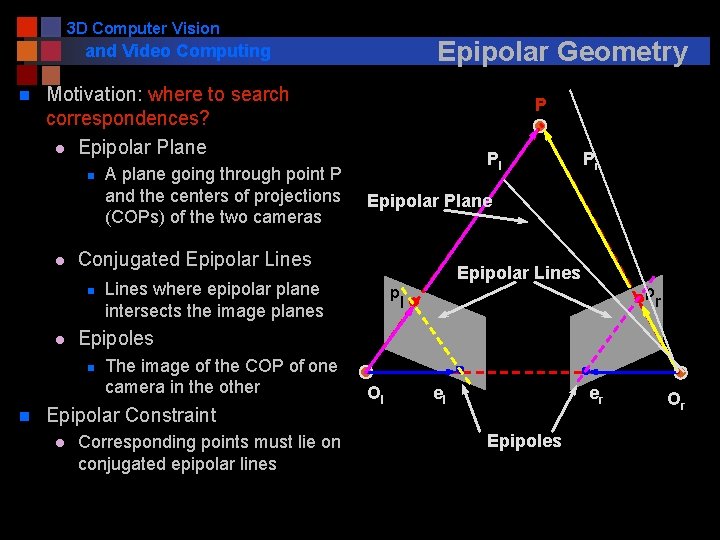
3 D Computer Vision Epipolar Geometry and Video Computing n Motivation: where to search correspondences? l Epipolar Plane n l Epipolar Plane Epipolar Lines where epipolar plane intersects the image planes The image of the COP of one camera in the other Epipolar Constraint l Pr p p l r Epipoles n n Pl Conjugated Epipolar Lines n l A plane going through point P and the centers of projections (COPs) of the two cameras P Corresponding points must lie on conjugated epipolar lines Ol el er Epipoles Or

3 D Computer Vision Essential Matrix and Video Computing n Equation of the epipolar plane l n Co-planarity condition of vectors Pl, T and Pl-T Essential Matrix l E = RS 3 x 3 matrix constructed from R and T (extrinsic only) n Rank (E) = 2, two equal nonzero singular values Rank (R) =3 Rank (S) =2

3 D Computer Vision and Video Computing

3 D Computer Vision and Video Computing n Essential Matrix E = RS l A natural link between the stereo point pair and the extrinsic parameters of the stereo system n n l One correspondence -> a linear equation of 9 entries Given 8 pairs of (pl, pr) -> E Mapping between points and epipolar lines we are looking for n n n Essential Matrix Given pl, E -> pr on the projective line in the right plane Equation represents the epipolar line of pr (or pl) in the right (or left) image Note: l pl, pr are in the camera coordinate system, not pixel coordinates that we can measure

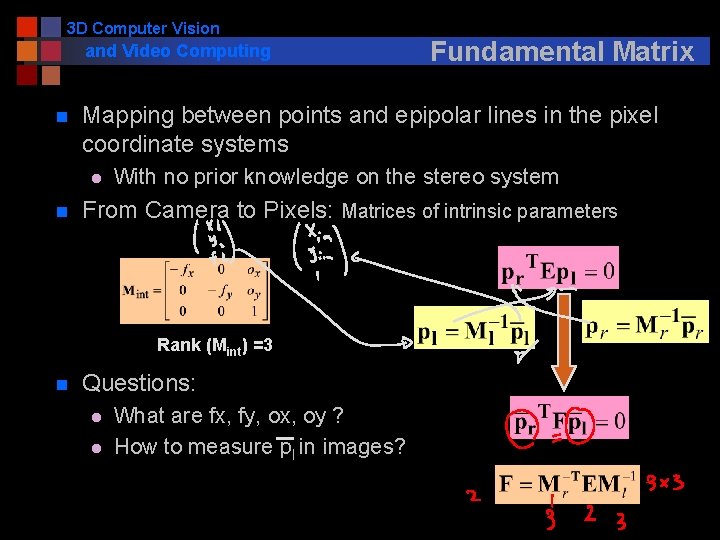
3 D Computer Vision and Video Computing n Mapping between points and epipolar lines in the pixel coordinate systems l n With no prior knowledge on the stereo system From Camera to Pixels: Matrices of intrinsic parameters Rank (Mint) =3 n Fundamental Matrix Questions: l l What are fx, fy, ox, oy ? How to measure pl in images?

3 D Computer Vision and Video Computing n Fundamental Matrix l l l Rank (F) = 2 Encodes info on both intrinsic and extrinsic parameters Enables full reconstruction of the epipolar geometry In pixel coordinate systems without any knowledge of the intrinsic and extrinsic parameters Linear equation of the 9 entries of F

3 D Computer Vision and Video Computing n Input: n point correspondences ( n >= 8) l Construct homogeneous system Ax= 0 from n n n l l x (up to a scale) is column of V corresponding to the least singular value Enforce singularity constraint: since Rank (F) = 2 n n x = (f 11, f 12, , f 13, f 21, f 22, f 23 f 31, f 32, f 33) : entries in F Each correspondence give one equation A is a nx 9 matrix Obtain estimate F^ by SVD of A n n F: The Eight-point Algorithm Compute SVD of F^ Set the smallest singular value to 0: D -> D’ Correct estimate of F : Output: the estimate of the fundamental matrix, F’ Similarly we can compute E given intrinsic parameters

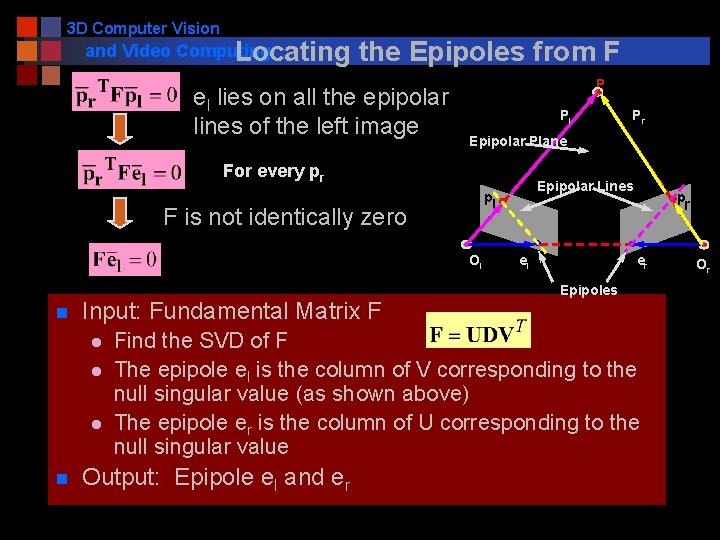
3 D Computer Vision and Video Computing Locating the Epipoles from F el lies on all the epipolar lines of the left image P Pl Epipolar Plane For every pr Ol Input: Fundamental Matrix F l l l n Epipolar Lines pl F is not identically zero n Pr p r el er Epipoles Find the SVD of F The epipole el is the column of V corresponding to the null singular value (as shown above) The epipole er is the column of U corresponding to the null singular value Output: Epipole el and er Or

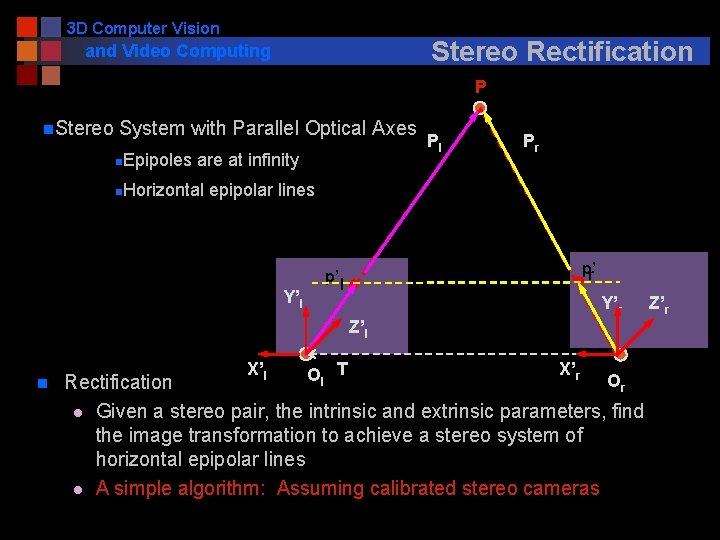
3 D Computer Vision Stereo Rectification and Video Computing P n. Stereo System with Parallel Optical Axes Epipoles are at infinity Pl Pr n Horizontal epipolar lines n Y’l p’ r p’ l Y’r Z’l n X’l Ol T X’r Or Rectification l Given a stereo pair, the intrinsic and extrinsic parameters, find the image transformation to achieve a stereo system of horizontal epipolar lines l A simple algorithm: Assuming calibrated stereo cameras Z’r

3 D Computer Vision and Video Computing n Stereo Rectification Algorithm l l Rotate both left and Pl right camera so that they share the same X axis : Or-Ol = T Define a rotation matrix Rrect for the left p Yl l camera Xl Rotation Matrix for Zl the right camera is X’l Ol T Rrect. RT R, T Rotation can be implemented by Xl’ = T, Yl’ = Xl’x. Zl, image transformation P Pr p r Yr Zr Or Xr Z’l = Xl’x. Yl’

3 D Computer Vision and Video Computing n Stereo Rectification Algorithm l l Rotate both left and Pl right camera so that they share the same X axis : Or-Ol = T Define a rotation matrix Rrect for the left p Yl l camera Xl Rotation Matrix for Zl the right camera is X’l Ol T Rrect. RT R, T Rotation can be implemented by Xl’ = T, Yl’ = Xl’x. Zl, image transformation P Pr p r Yr Zr Or Xr Z’l = Xl’x. Yl’

3 D Computer Vision and Video Computing n Stereo Rectification Algorithm l l Rotate both left and Pl right camera so that they share the same X axis : Or-Ol = T Define a rotation matrix Rrect for the left p’ l camera Y’l Rotation Matrix for Z’l the right camera is X’l Ol T Rrect. RT R, T Rotation can be implemented by T’ = (B, 0, 0), image transformation P Pr p’ r Y’r Z r X’r P’r = P’l – T’ Or

3 D Computer Vision and Video Computing n Purpose l n where to search correspondences Epipolar plane, epipolar lines, and epipoles l known intrinsic (f) and extrinsic (R, T) n l l co-planarity equation known intrinsic but unknown extrinsic n essential matrix unknown intrinsic and extrinsic n n Epipolar Geometry: Summary fundamental matrix Rectification l Generate stereo pair (by software) with parallel optical axis and thus horizontal epipolar lines

3 D Computer Vision and Video Computing Part n Three Questions l What to match? n l l Epipolar line? How to measure similarity? n Depends on features Approaches l l n Features: point, line, area, structure? Where to search correspondence? n n II. Correspondence problem Correlation-based approach Feature-based approach Advanced Topics l Image filtering to handle illumination changes l Adaptive windows to deal with multiple disparities l Local warping to account for perspective distortion l Sub-pixel matching to improve accuracy l Self-consistency to reduce false matches l Multi-baseline stereo

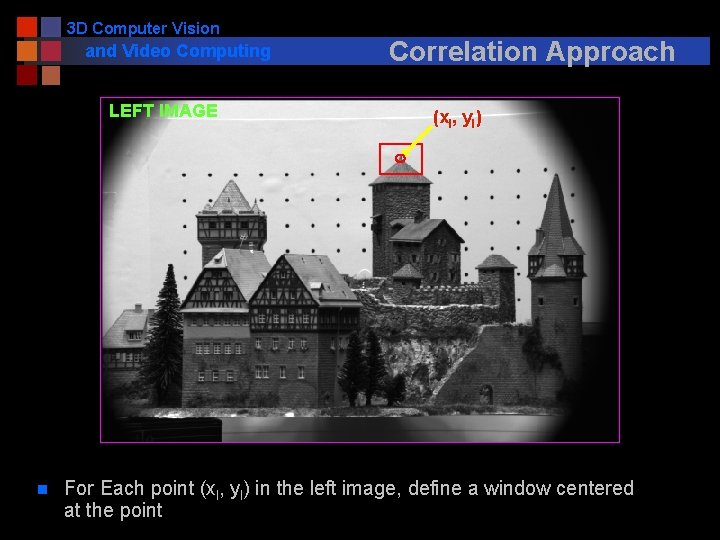
3 D Computer Vision and Video Computing LEFT IMAGE n Correlation Approach (xl, yl) For Each point (xl, yl) in the left image, define a window centered at the point

3 D Computer Vision and Video Computing RIGHT IMAGE n Correlation Approach (xl, yl) … search its corresponding point within a search region in the right image

3 D Computer Vision Correlation Approach and Video Computing RIGHT IMAGE n (xr, yr) dx (xl, yl) … the disparity (dx, dy) is the displacement when the correlation is maximum

3 D Computer Vision and Video Computing n Elements to be matched l n Image window of fixed size centered at each pixel in the left image Similarity criterion l l n Correlation Approach A measure of similarity between windows in the two images The corresponding element is given by window that maximizes the similarity criterion within a search region Search regions l l Theoretically, search region can be reduced to a 1 -D segment, along the epipolar line, and within the disparity range. In practice, search a slightly larger region due to errors in calibration

3 D Computer Vision and Video Computing n Equations n disparity n Similarity criterion Correlation Approach l Cross-Correlation l Sum of Square Difference (SSD) l Sum of Absolute Difference(SAD)

3 D Computer Vision and Video Computing n PROS l l l n Correlation Approach Easy to implement Produces dense disparity map Maybe slow CONS l l Needs textured images to work well Inadequate for matching image pairs from very different viewpoints due to illumination changes Window may cover points with quite different disparities Inaccurate disparities on the occluding boundaries

3 D Computer Vision and Video Computing n Correlation Approach A Stereo Pair of UMass Campus – texture, boundaries and occlusion

3 D Computer Vision and Video Computing n Features l l l n Feature-based Approach Edge points Lines (length, orientation, average contrast) Corners Matching algorithm l l l Extract features in the stereo pair Define similarity measure Search correspondences using similarity measure and the epipolar geometry

3 D Computer Vision and Video Computing Feature-based Approach LEFT IMAGE corner line structure n For each feature in the left image…

3 D Computer Vision and Video Computing Feature-based Approach RIGHT IMAGE corner line structure n Search in the right image… the disparity (dx, dy) is the displacement when the similarity measure is maximum

3 D Computer Vision and Video Computing n PROS l l n Feature-based Approach Relatively insensitive to illumination changes Good for man-made scenes with strong lines but weak texture or textureless surfaces Work well on the occluding boundaries (edges) Could be faster than the correlation approach CONS l l Only sparse depth map Feature extraction may be tricky n n Lines (Edges) might be partially extracted in one image How to measure the similarity between two lines?

3 D Computer Vision and Video Computing Advanced Topics n Mainly used in correlation-based approach, but can be applied to feature-based match n Image filtering to handle illumination changes l Image equalization n l To make two images more similar in illumination Laplacian filtering (2 nd order derivative) n Use derivative rather than intensity (or original color)

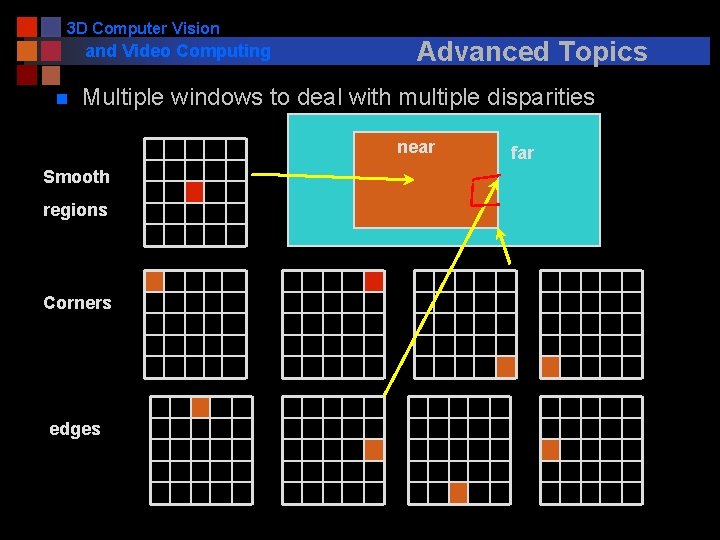
3 D Computer Vision and Video Computing n Advanced Topics Adaptive windows to deal with multiple disparities l Adaptive Window Approach (Kanade and Okutomi) n n l statistically adaptive technique which selects at each pixel the window size that minimizes the uncertainty in disparity estimates A Stereo Matching Algorithm with an Adaptive Window: Theory and Experiment, T. Kanade and M. Okutomi. Proc. 1991 IEEE International Conference on Robotics and Automation, Vol. 2, April, 1991, pp. 1088 -1095 Multiple window algorithm (Fusiello, et al) n n n Use 9 windows instead of just one to compute the SSD measure The point with the smallest SSD error amongst the 9 windows and various search locations is chosen as the best estimate for the given points A Fusiello, V. Roberto and E. Trucco, Efficient stereo with multiple windowing, IEEE CVPR pp 858 -863, 1997

3 D Computer Vision and Video Computing n Advanced Topics Multiple windows to deal with multiple disparities near Smooth regions Corners edges far

3 D Computer Vision and Video Computing Advanced Topics n Sub-pixel matching to improve accuracy l Find the peak in the correlation curves n Self-consistency to reduce false matches esp. for occlusions l Check the consistency of matches from L to R and from R to L n Multiple Resolution Approach l From coarse to fine for efficiency in searching correspondences n Local warping to account for perspective distortion l Warp from one view to the other for a small patch given an initial estimation of the (planar) surface normal n Multi-baseline Stereo l Improves both correspondences and 3 D estimation by using more than two cameras (images)

3 D Computer Vision and Video Computing n What we have done l l n 3 D Reconstruction Problem Correspondences using either correlation or feature based approaches Epipolar Geometry from at least 8 point correspondences Three cases of 3 D reconstruction depending on the amount of a priori knowledge on the stereo system l l l Both intrinsic and extrinsic known - > can solve the reconstruction problem unambiguously by triangulation Only intrinsic known -> recovery structure and extrinsic up to an unknown scaling factor Only correspondences -> reconstruction only up to an unknown, global projective transformation (*)

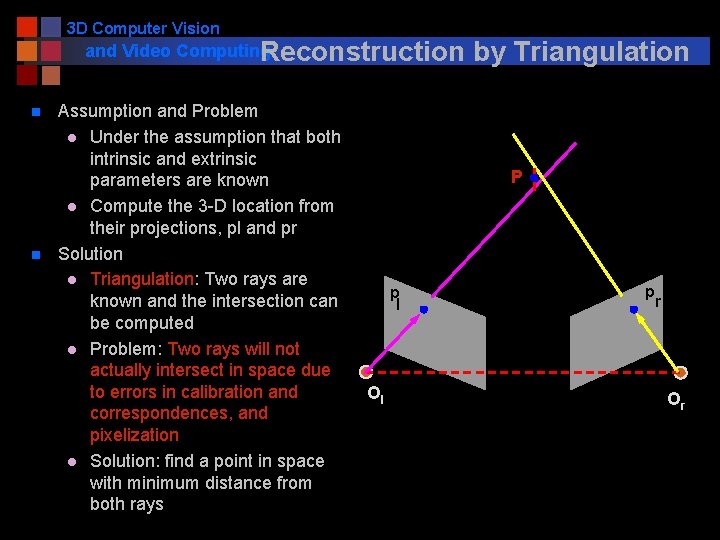
3 D Computer Vision and Video Computing Reconstruction n n Assumption and Problem l Under the assumption that both intrinsic and extrinsic parameters are known l Compute the 3 -D location from their projections, pl and pr Solution l Triangulation: Two rays are known and the intersection can be computed l Problem: Two rays will not actually intersect in space due to errors in calibration and correspondences, and pixelization l Solution: find a point in space with minimum distance from both rays by Triangulation P p l Ol p r Or

3 D Computer Vision and Video Computing Reconstruction n n up to a Scale Factor Assumption and Problem Statement l Under the assumption that only intrinsic parameters and more than 8 point correspondences are given l Compute the 3 -D location from their projections, pl and pr, as well as the extrinsic parameters Solution l Compute the essential matrix E from at least 8 correspondences l Estimate T (up to a scale and a sign) from E (=RS) using the orthogonal constraint of R, and then R n l l l End up with four different estimates of the pair (T, R) Reconstruct the depth of each point, and pick up the correct sign of R and T. Results: reconstructed 3 D points (up to a common scale); The scale can be determined if distance of two points (in space) are known

3 D Computer Vision and Video Computing Reconstruction up to a Projective Transformation (* not required for this course; needs advanced knowledge of projective geometry ) n Assumption and Problem Statement l l n Under the assumption that only n (>=8) point correspondences are given Compute the 3 -D location from their projections, pl and pr Solution l l Compute the Fundamental matrix F from at least 8 correspondences, and the two epipoles Determine the projection matrices n l Select five points ( from correspondence pairs) as the projective basis Compute the projective reconstruction n Unique up to the unknown projective transformation fixed by the choice of the five points

3 D Computer Vision and Video Computing n n n Summary Fundamental concepts and problems of stereo Epipolar geometry and stereo rectification Estimation of fundamental matrix from 8 point pairs Correspondence problem and two techniques: correlation and feature based matching Reconstruct 3 -D structure from image correspondences given l l l Fully calibrated Partially calibration Uncalibrated stereo cameras (*)

3 D Computer Vision Next and Video Computing n Understanding 3 D structure and events from motion Motion n. Homework #3 online, due Nov 15